 |
Произвольное отображение коники на себя (продолжение)
|
|
|
|
Теорема
Рассмотрим произвольное нецентральное проективное отображение коники на себя. Прямые, соединяющие соответствующие точки отображения, образуют линейную оболочку некоторой коники.
Чтобы доказать эту теорему, сведем случай произвольной коники к двум пересекающимся прямым. Выберем две произвольные прямые MM' и NN', соединяющие соответственные точки и покажем, что отображение коники на себя порождает отображение этих прямых друг на друга.
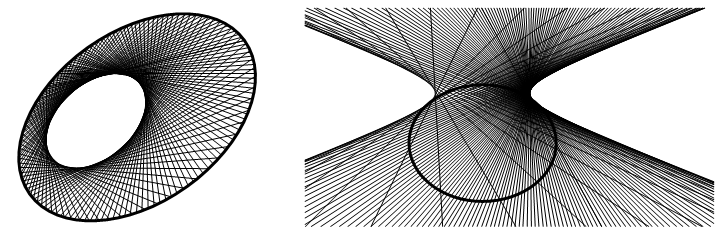
Заметим сначала, что прямые АВ' и А'В пересекаются в точке В0, лежащей на оси отображения s. Следовательно, точка В1, в которой пересекаются прямые АА' и ВВ', лежит на поляре точки В0.
 | |||
 | |||
Возьмем теперь произвольные точки М, А, В, С, D, и их четыре образа М' А', В', С', D'. По определению проективного отображения (AB, CD) = (A'B', C'D'). Теперь рассмотрим точки А1, В1, С1, D1 пересечения прямых АА', ВВ', СС' DD' с прямой ММ'.
Эти точки лежат на полярах точек А0, В0, С0, D0. Все эти поляры проходят через точку S, полюс оси s. При этом сложное отношение четырех поляр равно отношению полюсов (А0В0, С0D0).
Значит, (А0В0, С0D0) = (А1В1, С1D1), но по определению сложного отношения четырех точек коники, равному отношению четырех прямых, проходящих через точку М', (А0В0, С0D0) = (AB, CD). Значит, (А1В1, С1D1) = (AB, CD), и это равенство не зависит от выбора точек М и М'.
Выберем теперь две прямые ММ' и NN'. Получается, что для любой четверки прямых АА', ВВ', СС' DD' сложное отношение точек их пересечения с прямыми ММ' и NN' будет одним и тем же. Значит, отображение коники на себя порождает отображение прямой ММ' на прямую NN', откуда и следует утверждение теоремы.
Произвольное отображение коники на себя (продолжение)
|
|
|
Получается, что проективное отображение коники на себя порождает другую конику. Попробуем разобраться, как эти две коники связаны между собой. Если отображение имеет неподвижные точки, то дело обстоит достаточно просто. Касательная в неподвижной точке исходной коники является прямой, соединяющей соответственные точки отображения. Здесь мы считаем, что касательная «соединяет точку А с точкой А». Значит, эти касательные входят в линейную оболочку порожденной коники.
Получается, что порожденная коника касается исходной в двух неподвижных точках. Но если неподвижных точек нет, то коники вообще не имеют общих точек. Можно конечно сказать, что коники касаются в двух мнимых точках, но, к сожалению, предъявить эти точки на чертеже нельзя. Мнимые точки появляются внутри довольно сложной и абстрактной алгебраической модели. Область математики, исследующая свойства этих моделей, называется геометрией (землемерием) только в силу исторической традиции. Уравнениям, описывающим различные «геометрические» объекты давно уже не соответствуют никакие чертежи.
Если же мы хотим остаться в рамках «синтетической» геометрии (с чертежами), то придется сформулировать такое свойство взаимного расположения этих двух коник, которое не зависит от наличия точек пересечения.
 |
Заметим сначала, что прямая s, соединяющая неподвижные точки отображения – это его ось. Очевидно, полюсом этой прямой относительно обеих(! ) коник является точка пересечения общих касательных. Можно ожидать, что и в случае отсутствия общих точек ось отображения будет иметь один и тот же полюс относительно двух коник. И это действительно так.
Для доказательства заметим, что полюс и поляру связывают два взаимно двойственных построения. Поляра по известному полюсу строится с помощью вписанного четырехвершинника, полюс по известной поляре – с помощью описанного четырехсторонника. Идея доказательства – совместить эти два построения.
|
|
|
 |
Одно построение применим к исходной конике, заданной как множество точек, а второе – к порожденной конике, получившейся как линейная оболочка, то есть множество прямых. Покажем, что в результате для оси отображения получится один и тот же полюс.
Рассмотрим полюс S оси отображения относительно исходной коники. Нетрудно убедиться, что если выбрать на конике две точки А и В таких, что прямая АВ проходит через полюс S, и построить их образы А' и В', то прямая А'В' также будет проходить через этот полюс.
Действительно, прямые А'В и АВ' пересекаются на оси s. Поляра точки пересечения М проходит как через полюс S, так и через точку пересечения диагоналей АВ и А'В'. Но полюс уже лежит на прямой АВ, откуда и следует справедливость утверждения. Кроме того получаем, что и точка N пересечения АА' и ВВ' также лежит на оси s.
Прямые АА' и ВВ' входят в линейную оболочку порожденной коники, то есть являются касательными к ней. Построим теперь еще две касательных. Для этого применим отображение к точкам А' и В' и получим точки А'' и В''. Прямая А''В'' также проходит через полюс S, а прямые А'А'' и В'В'' касаются порожденной коники. При этом точка пересечения прямых А'А'' и В'В'' опять же лежит на оси s.
 |
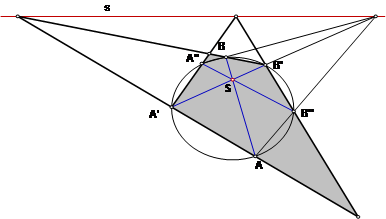Рассмотрим теперь четырехсторонник, образованный прямыми АА', ВВ', А'А'', В'В''. Его стороны касаются порожденной коники, а точки пересечения противоположных сторон лежат на оси s. Значит, его диагонали проходят через полюс прямой s относительно порожденной коники. Но одна из его диагоналей – прямая А'В'.
Значит, если прямая АВ проходит через полюс исходной коники, то прямая А'В' проходит через полюс порожденной коники. Применим это же утверждение к прямой А'В'. Поскольку она проходит через полюс исходной коники, то прямая А''В'' проходит через полюс порожденной коники. Значит полюс порожденной коники совпадает с точкой пересечения прямых А'В' и А''В'', то есть с точкой S. Что и требовалось доказать.
Верно и более сильное утверждение. Чтобы его сформулировать заметим, что любая коника порождает для любой прямой, не являющейся касательной, проективное отображение этой прямой на себя. Строится оно следующим образом:
|
|
|
Возьмем на прямой s произвольную точку А и построим ее поляру а. Точку А' пересечения поляры а с прямой s будем считать образом точки А.
Это отображение действительно является проективным, поскольку сложное отношение четырех точек прямой равно сложному отношению четырех их поляр.
 |
Кроме того, в силу принципа двойственности, если поляра точки А проходит через точку А', то и поляра точки А' проходит через точку А. Трехвершинник SАА' – автополярный. Значит, при данном отображении точка А' переходит обратно в точку А. Отображения, при которых точки обмениваются местами, называют инволюциями. Поэтому, отображение, которая коника порождает на прямой, называют инволюцией сопряженных точек.
Если прямая s пересекает конику, то инволюция меняет местами точки в парах, которые гармонически разделяют точки пересечения. Сами точки пересечения остаются на месте. Если же коника и прямая s не пересекаются, то инволюция не имеет неподвижных точек.
Возвращаясь к двум касающимся коникам – исходной и порожденной, сформулируем следующее утверждение:
Обе коники порождают на оси отображения одну и ту же инволюцию сопряженных точек.
Утверждение является вполне очевидным, если ось отображения пересекает исходную конику. Действительно, в этом случае инволюция однозначно задается двумя неподвижными точками. Для любой точки А прямой s ее образ строится, как четвертая гармоническая точка к ней самой и двум неподвижным точкам.
Если же коника и ось отображения не пересекаются, то придется доказать, что любая точка, лежащая на оси, имеет одну и ту же поляру относительно обеих коник.
 |
Заметим сначала, что если стороны четырехвершинника касаются коники, то его диагонали образуют автополярный трехвершинник, то есть каждая диагональ является полярой противоположной вершины. Применим это утверждение к двум коникам.
 |
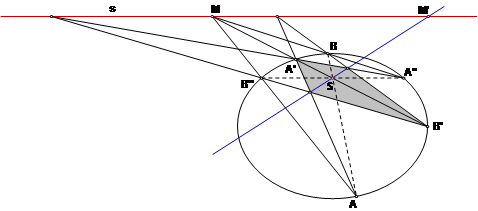Возьмем на оси отображения любую точку М и проведем прямую MS, точки ее пересечения с коникой обозначим А' и В'. Построим теперь точки А, В, А'', В'' (обозначения предыдущей теоремы). Получаем, что диагональ четырехсторонника, описанного вокруг порожденной коники, является полярой точки М. Та же диагональ SM' будет полярой точки М и относительно исходной коники. Это следует из того, что она проходит через точки пересечения прямых АА' и В'В'', ВВ' и А'А'', каждая из которых лежит на поляре.
|
|
|
Из того, что прямая SM' является полярой точки М относительно обеих коник следует, что обе коники порождают на оси s одну и ту же инволюцию сопряженных точек.
|
|
|
