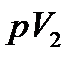I. Модуль полного комплексного сопротивления или полное сопротивление цепи
 (34)
(34)
При 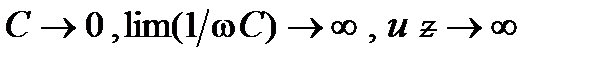
 данный случай соответствует обрыву в цепи, в месте соединения ёмкостного элемента. При
данный случай соответствует обрыву в цепи, в месте соединения ёмкостного элемента. При  (резонанс)
(резонанс)  т. е. сопротивление цепи достигает своего минимума и становится чисто активным. При
т. е. сопротивление цепи достигает своего минимума и становится чисто активным. При  это условие эквивалентно короткому замыканию участка схемы с С-элементом (
это условие эквивалентно короткому замыканию участка схемы с С-элементом ( – полное сопротивление катушки индуктивности). График функции
– полное сопротивление катушки индуктивности). График функции 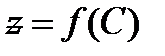 приведён на рис. 11.
приведён на рис. 11.
II. Действующее значение тока в цепи
 (35)
(35)
При  . Для резонансного режима ток достигает своего максимума
. Для резонансного режима ток достигает своего максимума
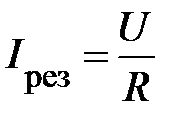
и в дальнейшем при С 
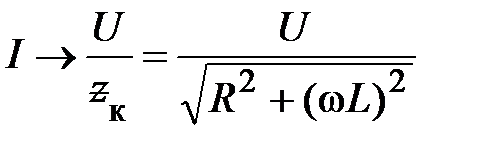 .
.
График зависимости  приведён на рис.10.
приведён на рис.10.
III. Действующее значение напряжения на С -элементе

При  . Для резонансного режима
. Для резонансного режима 

Наконец при  . Функция
. Функция  имеет максимум при условии
имеет максимум при условии
 . (36)
. (36)
Откуда можно определить значение С. График функции  приведён на рис. 10.
приведён на рис. 10.
IV. Действующее значение напряжения на L -элементе

При  . Для резонансного режима
. Для резонансного режима 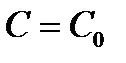

Наконец при 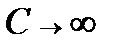

Данная функция достигает максимума при резонансе и график её изменения приведён на рис. 10.
V. Фазовый угол

При 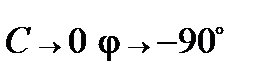 . В резонансном режиме
. В резонансном режиме 
 и, наконец, при
и, наконец, при 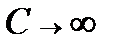 ,
,  График этой функции
График этой функции  приведён на рис. 12.
приведён на рис. 12.
На рис. 10, 13, 14 приведены графики функций:
– коэффициента мощности на зажимах цепи
 ; (37)
; (37)
– активной мощности на зажимах цепи
 ; (38)
; (38)
– напряжения на катушке индуктивности
 ; (39)
; (39)
– реактивной мощности на зажимах цепи
 . (40)
. (40)
Из рис. 10 видно, что в некотором интервале изменения С, включающем  ,
,

т. е. напряжения на реактивных элементах могут превышать общее напряжение в цепи. Учитывая, что при резонансе

Получим, что условие превышения падения напряжения на реактивных элементах при резонансе будет иметь место, если

Параметр, определяемый отношениями

называется добротностью резонансного контура. С учётом этого понятия

.
Если  , то имеет место ярко выраженный резонанс напряжений, если
, то имеет место ярко выраженный резонанс напряжений, если  , то при резонансе
, то при резонансе
 .
.
Последовательные резонансные цепи широко используются в электронной измерительной технике, в радиотехнике. Резонанс напряжений в электроэнергетических установках, как правило, не допустим из-за значительного увеличения тока в цепи, и может быть причиной аварии, поскольку активное сопротивление установок, как правило, незначительно.
ВЫВОДЫ
Цепь однофазного синусоидального тока с последовательно включёнными R, L, C -элементами характеризуется тем, что полное сопротивление цепи слагается из:
– активного сопротивления R;
– положительного индуктивного сопротивления 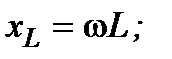
– отрицательного ёмкостного сопротивления 
 .
.
Величина  определяется выражением
определяется выражением
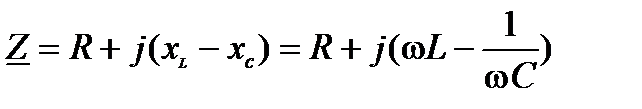 .
.
Реактивное сопротивление  может быть, как положительным числом
может быть, как положительным числом 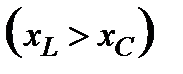 , так и отрицательным
, так и отрицательным  или равным нулю
или равным нулю  . Т. е. индуктивное и ёмкостное сопротивления частично или полностью компенсируют друг друга.
. Т. е. индуктивное и ёмкостное сопротивления частично или полностью компенсируют друг друга.
Угол сдвига фаз φ полностью определяется величиной и соотношением сопротивлений элементов
 .
.
В зависимости от этих условий он может быть положительным, если  , в этом случае ток в цепи будет отставать по фазе на угол φ от общего напряжения. Угол φ может быть отрицательным, при
, в этом случае ток в цепи будет отставать по фазе на угол φ от общего напряжения. Угол φ может быть отрицательным, при  , т. е. ток в цепи будет опережать по фазе, указанное напряжение. Наконец, угол φ может быть равным нулю, если
, т. е. ток в цепи будет опережать по фазе, указанное напряжение. Наконец, угол φ может быть равным нулю, если  . В этом случае ток и рассматриваемое напряжение совпадают по фазе.
. В этом случае ток и рассматриваемое напряжение совпадают по фазе.
Ток в цепи определяется соотношением
 ,
,
которое является выражением закона Ома для данной цепи в действующих значениях параметров режима.
При условии, что  и вектор
и вектор  расположен вдоль оси +1 на комплексной плоскости, выражение для тока в комплексной форме имеет вид
расположен вдоль оси +1 на комплексной плоскости, выражение для тока в комплексной форме имеет вид
 .
.
Вектор тока  может располагаться в четвертой четверти (φ>0), в первой четверти (φ<0) или совпадать по направлению с
может располагаться в четвертой четверти (φ>0), в первой четверти (φ<0) или совпадать по направлению с  (φ=0).
(φ=0).
Напряжения на реактивных элементах определяются их сопротивлениями и сдвинуты относительно друг друга по фазе 180º. Т. е. в цепи происходит частичная ( ) или полная (
) или полная ( ) компенсация реактивной составляющей общего напряжения
) компенсация реактивной составляющей общего напряжения
 .
.
При этом вектора  и
и  направлены на векторной диаграмме в противоположные стороны.
направлены на векторной диаграмме в противоположные стороны.
Интенсивность энергетических процессов определяется
· величиной активной мощности
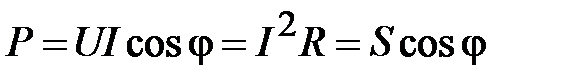 , Ватт,
, Ватт,
которая определяет скорость необратимого преобразования электрической энергии (интенсивность изменения этой энергии) в неэлектрические виды энергии на R -элементе;
· величиной реактивной мощности
 , Вар,
, Вар,
которая определяет скорость изменения циркулирующей энергии (интенсивность изменения этой энергии) между полями L, C -элементов и источником питания. Эта мощность, в свою очередь, определяется разностью реактивных мощностей на L -элементе ( ) и С -элементе (
) и С -элементе ( ).
).
Указанные реактивные мощности могут частично компенсировать друг друга ( при
при  или
или  при
при  ) или происходит полная компенсация мощностей
) или происходит полная компенсация мощностей  и
и  (
( при
при  ). В этом случае мощность на этом участке цепи чисто активная
). В этом случае мощность на этом участке цепи чисто активная

Справочные данные
Для измерения активной мощности в цепях синусоидального тока используются специальные приборы: ваттметры электродинамической системы, которые имеют 2 измерительные цепи. Одна из них (так называемая токовая цепь  ) включается последовательно с нагрузкой (рис. 5), ток в этой цепи I равен току в нагрузке. Другая цепь (так называемая потенциальная
) включается последовательно с нагрузкой (рис. 5), ток в этой цепи I равен току в нагрузке. Другая цепь (так называемая потенциальная  ) включается параллельно нагрузке, т. е. напряжение на этой цепи равно напряжению на нагрузке. Чтобы правильно учесть угол сдвига фаз φ, измерительные цепи ваттметра должны быть аналогично включены относительно положительных направлений напряжения и тока в нагрузке. Для этого один из зажимов цепи помечен звёздочкой (*). Правильное включение ваттметра при измерении мощности на нагрузке приведено на рис. 15.
) включается параллельно нагрузке, т. е. напряжение на этой цепи равно напряжению на нагрузке. Чтобы правильно учесть угол сдвига фаз φ, измерительные цепи ваттметра должны быть аналогично включены относительно положительных направлений напряжения и тока в нагрузке. Для этого один из зажимов цепи помечен звёздочкой (*). Правильное включение ваттметра при измерении мощности на нагрузке приведено на рис. 15.
При снятии показаний с ваттметра необходимо определить цену деления. Она рассчитывается по формуле
 , Вт/дел,
, Вт/дел,
где  – предел измерения по напряжению (устанавливается переключателем пределов слева на панели прибора);
– предел измерения по напряжению (устанавливается переключателем пределов слева на панели прибора);
 – предел измерения по току (устанавливается переключателем пределов справа на панели прибора);
– предел измерения по току (устанавливается переключателем пределов справа на панели прибора);
N – число делений измерительной шкалы ваттметра.
Порядок выполнения работы
Работа состоит из двух этапов. На первом проводят исследования режимов работы катушки индуктивности и конденсатора в отдельности. На втором при последовательном включении этих элементов.
1. Собрать цепь с катушкой индуктивности согласно рис. 16, сопротивление R реостата подобрать по указанию преподавателя. Также по указанию преподавателя установить первоначальное значение напряжения источника питания. Замкнуть ключ К и снять показания приборов. Повторить опыт 3 – 4 раза, меняя напряжение источника питания. Результаты занести в табл. 1.
2. Разомкнуть ключ К и установить максимальное сопротивление реостата R. При неизменном напряжении питания (по указанию преподавателя) снять показания приборов и занести в табл. 1. Плавно уменьшая сопротивление реостата провести 3 опыта, снять показания приборов и занести данные измерений в табл. 1.
3. Для первых опытов, при условии замкнутого ключа определить значение 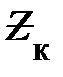 – полное и
– полное и  – активное сопротивление катушки индуктивности и вычислить среднее их значение
– активное сопротивление катушки индуктивности и вычислить среднее их значение
 ;
;  ;
; 
Рассчитать величину xL, L для каждого опыта и определить среднее их значение по формулам

 ;
;  .
.
3. Собрать схему с батареей конденсаторов и реостатом (рис. 17). Произвести измерения при условиях, аналогичных пунктам 1 и 2. Занести результаты измерений в таблицу 2.
4. Собрать схему с последовательным соединением батареи конденсаторов и катушки индуктивности (рис. 18). Установить по заданию преподавателя необходимое напряжение источника питания U. Исследование проводить по следующей методике:
а). Провести опыт резонанса напряжений. Рассчитать величину  по формуле
по формуле
 .
.
Величина  рассчитана в пункте 2,
рассчитана в пункте 2,  (рад/с). Выбрать с помощью батареи конденсаторов ближайшее к
(рад/с). Выбрать с помощью батареи конденсаторов ближайшее к  значение емкости. То есть установить значение
значение емкости. То есть установить значение  , снять показания приборов и занести данные измерений в табл. 3.
, снять показания приборов и занести данные измерений в табл. 3.
б). Каждый раз уменьшая предыдущее значение мощности на величину 2 – 4 мкФ, повести 2 – 3 опыта и записать показания в табл. 3.
в). Восстановить значение  и, каждый раз увеличивая предыдущее значение ёмкости на 2 – 4 мкФ, провести 2 – 3 опыта. Результаты измерений записать в табл. 3.
и, каждый раз увеличивая предыдущее значение ёмкости на 2 – 4 мкФ, провести 2 – 3 опыта. Результаты измерений записать в табл. 3.
г). Определить максимальные значения параметров при изменении  . Устанавливая на батарее конденсаторов значение ёмкости наиболее близкое к значению
. Устанавливая на батарее конденсаторов значение ёмкости наиболее близкое к значению

определить U C max. Устанавливая значения емкости близкие к значениям

 ,
,
измерить параметры  и с их помощью по формуле (40) экстремальные значения реактивной мощности.
и с их помощью по формуле (40) экстремальные значения реактивной мощности.
5). Произвести расчет всех параметров в табл. 1, 2, 3 по формулам, приведенным в работе.
Примечание. В табл. №3 приведены два столбца, определяющие емкость батареи конденсаторов: C и C ист. В ячейках столбца C указывают величину емкости, набранную на батарее конденсаторов непосредственно перед каждым опытом. В ячейках столбца C ист указывают истинное значение емкости, которое определяют по формуле  после проведения опытов.
после проведения опытов.
6). Построить комплекты векторных диаграмм (треугольники сопротивлений напряжений и мощностей, а также вектор тока, соответствующие одному и тому же опыту, в одной системе комплексных координат, но в разных масштабах). Для данных в таблицах 1 и 2 каждому студенту построить по два комплекта векторных диаграмм, соответствующих опыту при замкнутом ключе и при разомкнутом ключе (номера опытов задаются преподавателем). Для данных в таблице 3 каждому студенту необходимо построить по три комплекта векторных диаграмм (треугольники напряжений и вектор тока), соответствующих дорезонансному ( ), резонансному (
), резонансному ( ) и зарезонансному (
) и зарезонансному ( ) режимам работы цепи.
) режимам работы цепи.
7). Построить по данным табл. №3 графики зависимостей параметров режима работы цепи от изменения емкости конденсаторов (рис. 10 – 14).
Рекомендуемая литература
1. Электротехника. Учебн. для неэлектротехнич. спец. ВУЗов / Под ред. В. Г. Герасимова. М.: Высшая школа, 1985 (подраздел 2.12).
2. Касаткин А. С., Немцов М. В. Электротехника: Учебн. пособие для ВУЗов. М.: Издательский центр «Академия». 2005, (подразделы 2.11, 2.12, 2.13, 2.14, 2.21).
3. Общая электротехника / Под ред. А. Т. Блажкина. Л.: Энергоатомиздат. 1986, п.п. 2.7, 2.10.
4. Борисов Ю. М., Липатов Д. Н., Зорин Ю.Н. Электротехника: Учебн. Для ВУЗов. М.: Энергоатомиздат. 1985 (подразделы 2.9, 2.10, 2.11, 2.12).
Контрольные вопросы
1. Какие сопротивления называются реактивными и почему?
2. Что такое параметры катушки индуктивности, конденсатора. Как они определяются?
3. Какие энергетические процессы протекают в цепи с последовательным соединением R, L, C - элементов?
4. Какие энергетические процессы протекают в цепи с последовательным соединением R, L -элементов (R, C - элементов)?
5. Объяснить на примере порядок построения векторных диаграмм для цепи с последовательным соединением R, L, C - элементов.
6. Провести анализ построенных по заданию лабораторной работы векторных диаграмм.
7. Провести анализ построенных по заданию лабораторной работы графиков.
8. Сформулировать условие резонанса и определить параметры режима работы каждого элемента при резонансе напряжений.
9. Дана электрическая цепь с последовательным соединением R, L, C - элементов, которая подключена под напряжение u = 400sin(314 t), В. Решить задачу для одного из вариантов по заданию преподавателя:
– R =20, Ом, L =96, мГн, С =53, мкФ. Найти I; UL; UC; φ; – R =100, Ом, L =191, мГн, С =53, мкФ. Найти I; cosφ;  ; P; Q; S; – R =80, Ом, L =144, мГн, С=26,5, мкФ. Найти I; UL; UC; Q; P; S;
; P; Q; S; – R =80, Ом, L =144, мГн, С=26,5, мкФ. Найти I; UL; UC; Q; P; S;
10. Дана электрическая цепь с последовательным соединением R, L, C - элементов. Вольтметры, измеряющие падение напряжения на элементах, показали следующие значения:
– UR =100, В, UL =40, B, UC =70, В; – UR =200 В, UL =180 B, UC =90 В;
– UR =50 В, UL =200 B, Uc = UC В.
Найти общее напряжение на зажимах цепи и угол сдвига фаз между напряжением и током. Решить задачу для одного из вариантов по заданию преподавателя.
Рис.1.
Рис. 2.
Рис. 3.
Рис. 4.
Рис. 5.
Рис. 6.
Рис. 7.
Рис. 8
Рис. 9.
Рис. 10.
Рис. 11.
Рис. 12.
Рис. 13
Рис. 14.
 и
и  определяются из условия
определяются из условия
 .
.
Рис. 15.
Рис. 16.
Рис. 17.
Рис. 18.
Таблица 1.
Воспользуйтесь поиском по сайту:


 (34)
(34)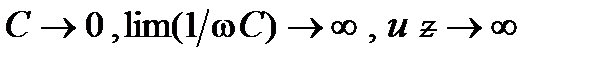
 данный случай соответствует обрыву в цепи, в месте соединения ёмкостного элемента. При
данный случай соответствует обрыву в цепи, в месте соединения ёмкостного элемента. При  (резонанс)
(резонанс)  т. е. сопротивление цепи достигает своего минимума и становится чисто активным. При
т. е. сопротивление цепи достигает своего минимума и становится чисто активным. При  это условие эквивалентно короткому замыканию участка схемы с С-элементом (
это условие эквивалентно короткому замыканию участка схемы с С-элементом ( – полное сопротивление катушки индуктивности). График функции
– полное сопротивление катушки индуктивности). График функции 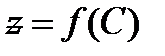 приведён на рис. 11.
приведён на рис. 11. (35)
(35) . Для резонансного режима ток достигает своего максимума
. Для резонансного режима ток достигает своего максимума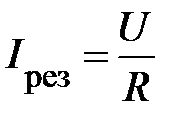

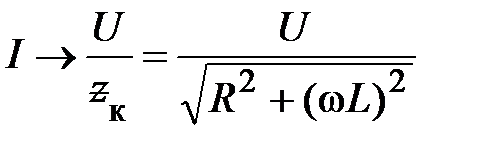 .
. приведён на рис.10.
приведён на рис.10.
 . Для резонансного режима
. Для резонансного режима 

 . Функция
. Функция  имеет максимум при условии
имеет максимум при условии . (36)
. (36) приведён на рис. 10.
приведён на рис. 10.
 . Для резонансного режима
. Для резонансного режима 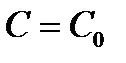

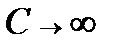


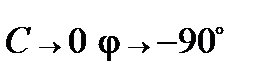 . В резонансном режиме
. В резонансном режиме 
 и, наконец, при
и, наконец, при 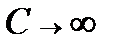 ,
,  График этой функции
График этой функции  приведён на рис. 12.
приведён на рис. 12. ; (37)
; (37) ; (38)
; (38) ; (39)
; (39) . (40)
. (40) ,
,



 .
.
 , то имеет место ярко выраженный резонанс напряжений, если
, то имеет место ярко выраженный резонанс напряжений, если  , то при резонансе
, то при резонансе .
.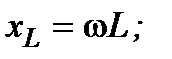

 .
. определяется выражением
определяется выражением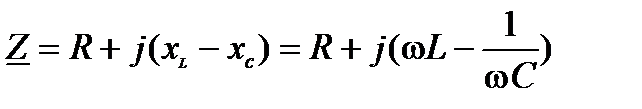 .
. может быть, как положительным числом
может быть, как положительным числом 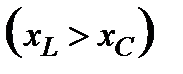 , так и отрицательным
, так и отрицательным  или равным нулю
или равным нулю  . Т. е. индуктивное и ёмкостное сопротивления частично или полностью компенсируют друг друга.
. Т. е. индуктивное и ёмкостное сопротивления частично или полностью компенсируют друг друга. .
. , в этом случае ток в цепи будет отставать по фазе на угол φ от общего напряжения. Угол φ может быть отрицательным, при
, в этом случае ток в цепи будет отставать по фазе на угол φ от общего напряжения. Угол φ может быть отрицательным, при  , т. е. ток в цепи будет опережать по фазе, указанное напряжение. Наконец, угол φ может быть равным нулю, если
, т. е. ток в цепи будет опережать по фазе, указанное напряжение. Наконец, угол φ может быть равным нулю, если  . В этом случае ток и рассматриваемое напряжение совпадают по фазе.
. В этом случае ток и рассматриваемое напряжение совпадают по фазе. ,
, и вектор
и вектор  расположен вдоль оси +1 на комплексной плоскости, выражение для тока в комплексной форме имеет вид
расположен вдоль оси +1 на комплексной плоскости, выражение для тока в комплексной форме имеет вид .
. может располагаться в четвертой четверти (φ>0), в первой четверти (φ<0) или совпадать по направлению с
может располагаться в четвертой четверти (φ>0), в первой четверти (φ<0) или совпадать по направлению с  (φ=0).
(φ=0). ) или полная (
) или полная ( ) компенсация реактивной составляющей общего напряжения
) компенсация реактивной составляющей общего напряжения .
. и
и  направлены на векторной диаграмме в противоположные стороны.
направлены на векторной диаграмме в противоположные стороны.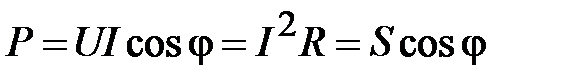 , Ватт,
, Ватт, , Вар,
, Вар, ) и С -элементе (
) и С -элементе ( ).
). при
при  или
или  при
при  ) или происходит полная компенсация мощностей
) или происходит полная компенсация мощностей  и
и  (
( при
при  ). В этом случае мощность на этом участке цепи чисто активная
). В этом случае мощность на этом участке цепи чисто активная
 ) включается последовательно с нагрузкой (рис. 5), ток в этой цепи I равен току в нагрузке. Другая цепь (так называемая потенциальная
) включается последовательно с нагрузкой (рис. 5), ток в этой цепи I равен току в нагрузке. Другая цепь (так называемая потенциальная  ) включается параллельно нагрузке, т. е. напряжение на этой цепи равно напряжению на нагрузке. Чтобы правильно учесть угол сдвига фаз φ, измерительные цепи ваттметра должны быть аналогично включены относительно положительных направлений напряжения и тока в нагрузке. Для этого один из зажимов цепи помечен звёздочкой (*). Правильное включение ваттметра при измерении мощности на нагрузке приведено на рис. 15.
) включается параллельно нагрузке, т. е. напряжение на этой цепи равно напряжению на нагрузке. Чтобы правильно учесть угол сдвига фаз φ, измерительные цепи ваттметра должны быть аналогично включены относительно положительных направлений напряжения и тока в нагрузке. Для этого один из зажимов цепи помечен звёздочкой (*). Правильное включение ваттметра при измерении мощности на нагрузке приведено на рис. 15. , Вт/дел,
, Вт/дел, – предел измерения по напряжению (устанавливается переключателем пределов слева на панели прибора);
– предел измерения по напряжению (устанавливается переключателем пределов слева на панели прибора); – предел измерения по току (устанавливается переключателем пределов справа на панели прибора);
– предел измерения по току (устанавливается переключателем пределов справа на панели прибора);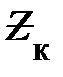 – полное и
– полное и  – активное сопротивление катушки индуктивности и вычислить среднее их значение
– активное сопротивление катушки индуктивности и вычислить среднее их значение ;
;  ;
; 

 ;
;  .
. по формуле
по формуле .
. рассчитана в пункте 2,
рассчитана в пункте 2,  (рад/с). Выбрать с помощью батареи конденсаторов ближайшее к
(рад/с). Выбрать с помощью батареи конденсаторов ближайшее к  значение емкости. То есть установить значение
значение емкости. То есть установить значение  , снять показания приборов и занести данные измерений в табл. 3.
, снять показания приборов и занести данные измерений в табл. 3. и, каждый раз увеличивая предыдущее значение ёмкости на 2 – 4 мкФ, провести 2 – 3 опыта. Результаты измерений записать в табл. 3.
и, каждый раз увеличивая предыдущее значение ёмкости на 2 – 4 мкФ, провести 2 – 3 опыта. Результаты измерений записать в табл. 3. . Устанавливая на батарее конденсаторов значение ёмкости наиболее близкое к значению
. Устанавливая на батарее конденсаторов значение ёмкости наиболее близкое к значению

 ,
, и с их помощью по формуле (40) экстремальные значения реактивной мощности.
и с их помощью по формуле (40) экстремальные значения реактивной мощности. после проведения опытов.
после проведения опытов. ), резонансному (
), резонансному ( ) и зарезонансному (
) и зарезонансному ( ) режимам работы цепи.
) режимам работы цепи. ; P; Q; S; – R =80, Ом, L =144, мГн, С=26,5, мкФ. Найти I; UL; UC; Q; P; S;
; P; Q; S; – R =80, Ом, L =144, мГн, С=26,5, мкФ. Найти I; UL; UC; Q; P; S;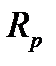
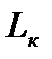













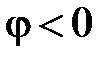











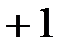







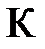







































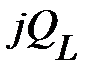











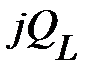


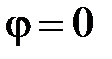













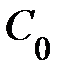
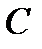




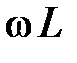




















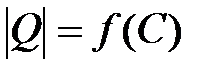

 и
и  определяются из условия
определяются из условия .
.