 |
Основные теоретические положения
|
|
|
|
Трёхфазными электрическими цепями называются объединённые в одну три подобные цепи, в каждой из которых действует свой источник энергии переменного тока. Все три источника являются независимыми и имеют одинаковую частоту ЭДС. ЭДС этих источников, как правило, одинаковы по амплитуде, но сдвинуты по фазе друг относительно друга на 120º (2π/3). Объединяемые цепи принято называть фазами трёхфазной цепи.
В электротехнике термин “фаза” применяется в двух различных смыслах: во-первых, это аргумент синусоидальной функции времени (ω t +ψ), а во-вторых, наименование составной части трёхфазной цепи.
Как правило, источники энергии трёхфазной цепи конструктивно объединены в одном электротехническом устройстве, называемом трёхфазным генератором. Все элементы трёхфазного генератора, относящиеся к одному из трёх независимых источников энергии, принято называть фазой генератора. Эти источники энергии можно представить в виде источников ЭДС (рис.1). Зажимы фаз генератора, в сторону которых направлены положительные направления ЭДС, принято называть началами фаз генератора (A, B, C на рис. 1). Другие зажимы – концами фаз генератора (X, Y, Z). При этом участки цепи 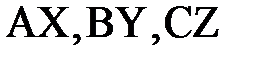 называют фазами генератора. Если принять начальную фазу ЭДС генератора
называют фазами генератора. Если принять начальную фазу ЭДС генератора  равной нулю, то можно записать выражения для мгновенных значений всех ЭДС в виде
равной нулю, то можно записать выражения для мгновенных значений всех ЭДС в виде
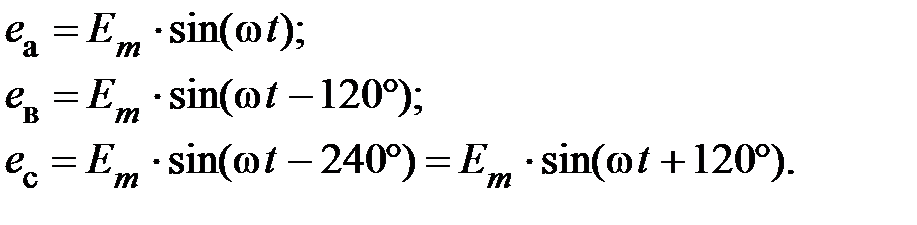 (1)
(1)
Такая система ЭДС называется трехфазной симметричной системой. Последовательность в обозначении фаз генератора, т. е. порядок чередования фаз, не может быть случайной. Например, последовательность, приведённую в (1) называют прямой последовательностью фаз. Для такой последовательности характерно, что ЭДС фазы В отстаёт от ЭДС фазы А на угол 120º, а ЭДС фазы С отстаёт от ЭДС фазы В также на угол 120º. Если поменять местами любые две фазы, то полученная новая последовательность будет называться обратной последовательностью фаз. Соотношение (1) можно представить в комплексной форме
|
|
|
 (2)
(2)
где 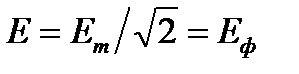 – модуль фазной ЭДС генератора (конкретное действующее значение синусоидальной фазной ЭДС). Представим последние два соотношения в алгебраической форме
– модуль фазной ЭДС генератора (конкретное действующее значение синусоидальной фазной ЭДС). Представим последние два соотношения в алгебраической форме
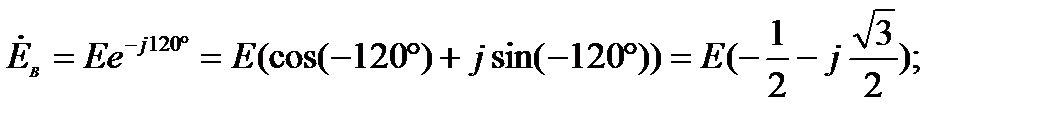 (3)
(3)
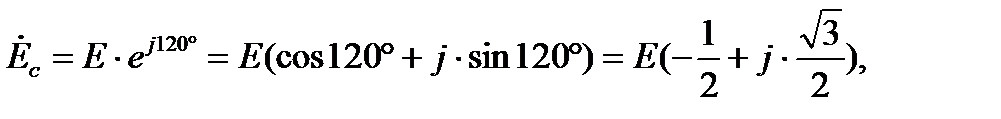
и сложим (3) и первое равенство (2) вместе
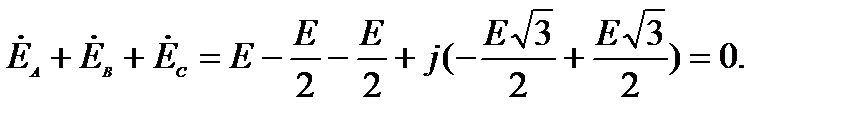 (4)
(4)
Равенство (4) справедливо в любой момент времени, следовательно:
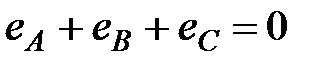 . (5)
. (5)
Таким образом, алгебраическая сумма мгновенных значений фазных ЭДС генератора равна нулю в любой момент времени. Это условие вытекает непосредственно из закона сохранения заряда и свидетельствует, что в генераторе абсолютная величина заряда всегда равна нулю.
Изобразим соотношения (2) на комплексной плоскости (рис. 2). При этом видно, что сумма векторов также равна нулю.
Для того, чтобы получить трёхфазную цепь, необходимо фазы генератора соединить с трёхфазным приёмником (нагрузкой). Наиболее естественно каждую фазу генератора можно соединить с соответствующей фазой нагрузки двумя соединительными проводами. В результате получим шестипроводную несвязанную трёхфазную цепь. Такие цепи на практике не используются, как неэкономичные. Для уменьшения числа проводов линии электропередачи необходимо электрически соединить определенные зажимы фаз генератора между собой и, аналогично, фаз нагрузки.
Рассмотрим в данной работе соединение указанных элементов трёхфазной цепи по схеме звезда (). При таком соединении концы фаз генератора и отдельно нагрузки объединяются в общий узел: со стороны генератора – N (рис. 3) и со стороны нагрузки – n. Начала фаз генератора и приёмника присоединяются к линейным проводам. Узлы N и n называются нейтральными точками, а провод их соединяющий нейтральным проводом. Полученная трёхфазная цепь называется четырёхпроводной цепью. Рассмотрим на примере этой цепи основные элементы трёхфазной цепи и характерные для неё параметры режима работы. Провода, соединяющие начала фаз генератора и приёмника (Аа, Вв, Сс), называются линейными проводами. Участок цепи А,а,n,N называется фазой А. Аналогично можно определить участки, соответствующие фазам В и С. Участки цепи AN, BN, CN называются фазами со стороны генератора, участки an, bn, cn – фазами со стороны нагрузки.
|
|
|
Разность потенциалов между началом и концом фазы со стороны нагрузки называется фазным напряжением. Так  есть фазные напряжения со стороны нагрузки. Разность потенциалов между линейными проводами называется линейным напряжением. Будем считать незначительными сопротивления линейных и нейтрального проводов. Т. е.
есть фазные напряжения со стороны нагрузки. Разность потенциалов между линейными проводами называется линейным напряжением. Будем считать незначительными сопротивления линейных и нейтрального проводов. Т. е.
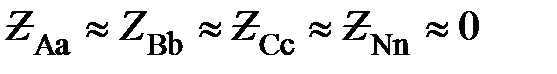 . (6)
. (6)
В этом случае потери напряжения в линиях и в нейтральном проводе
 (7)
(7)
и линейные напряжения вдоль линии не изменяются. На рис. 3  – линейные напряжения;
– линейные напряжения; 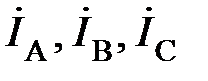 – линейные токи;
– линейные токи; 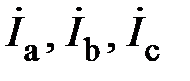 – токи в фазах нагрузки;
– токи в фазах нагрузки; 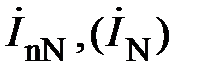 – ток в нейтральном проводе;
– ток в нейтральном проводе; 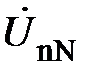 – напряжение смещения нейтрали.
– напряжение смещения нейтрали.
С учётом (6) и (7) для контура фазы А можно составить уравнение по второму закону Кирхгофа (контур обозначен сплошной кривой со стрелкой)
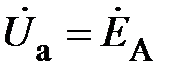 ;
;
Аналогично
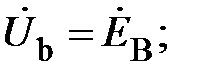
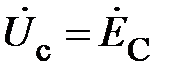 . (8)
. (8)
Следовательно, векторная диаграмма на рис. 2 будет отвечать и фазным напряжениям.
Для контура, обход которого обозначен штриховой линией, будет иметь
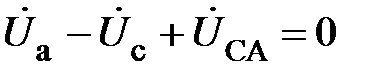
или
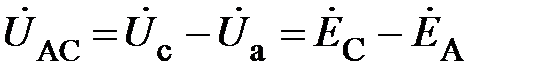 . (9)
. (9)
Аналогично
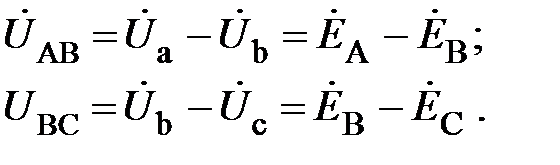 (10)
(10)
Соотношения (9) и (10) устанавливают связь между линейными и фазными напряжениями при любом режиме работы данной трёхфазной цепи. Изобразим эти соотношения на комплексной плоскости (рис. 4). Из рис.4 видно, что модули фазных (U ф) и линейных (U л) напряжений связаны соотношением
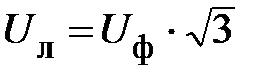 . (11)
. (11)
Ток в нейтральном проводе, согласно 1 закона Кирхгофа (для узла n) определится
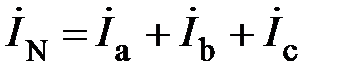 . (12)
. (12)
Все элементы электрической цепи в каждой фазе соединены последовательно, т. е. линейный ток равен соответствующему фазному току
|
|
|
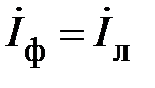 . (13)
. (13)
Если в трехфазную цепь включен приемник и сопротивления его фаз равны
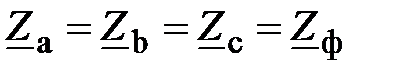 , (14)
, (14)
то такой приемник называют симметричным. Режим работы цепи также будет симметричным. При этом фазные токи
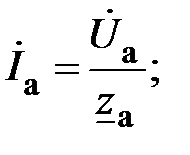

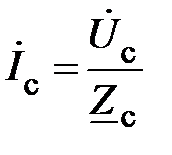 (15)
(15)
равны по модулю
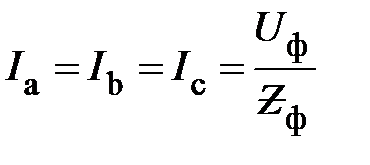 (16)
(16)
и сдвинуты по фазе относительно соответствующего фазного напряжения по один и тот же угол
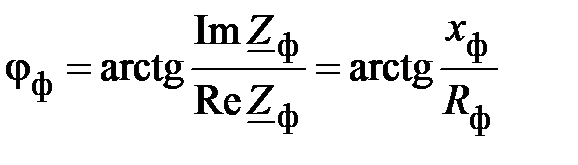 . (17)
. (17)
где  и
и  соответственно, активное и реактивное сопротивления каждой фазы. На рис.4, в качестве примера, показаны вектора фазных токов для активно-индуктивной нагрузки фазы. Они образуют трёхфазную симметричную систему векторов и, согласно (4), их сумма равна нулю
соответственно, активное и реактивное сопротивления каждой фазы. На рис.4, в качестве примера, показаны вектора фазных токов для активно-индуктивной нагрузки фазы. Они образуют трёхфазную симметричную систему векторов и, согласно (4), их сумма равна нулю
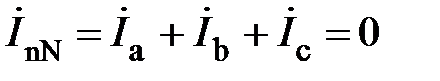 . (18)
. (18)
Т. е. при симметричном режиме работы четырёхпроводной трёхфазной цепи ток в нейтральном проводе отсутствует, и необходимость в этом проводе отпадает.
Если в трехфазную цепь включен несимметричный приемник (условие (14) не соблюдается), то режим работы цепи будет также несимметричным. При несимметричном режиме работы четырёхпроводной цепи, условие (14) нарушается, но остаётся справедливым условие (8). Т. е. благодаря нейтральному проводу фазные напряжения будут равны соответствующим фазным ЭДС генератора. Следовательно, нейтральный провод обеспечивает сохранение симметрии фазных напряжений несимметричного приёмника.
В то же время токи в каждой фазе, рассчитываемые по соотношениям (15), уже не будут образовывать трехфазную симметричную систему
 .
.
Поэтому в нейтральном проводе будет протекать ток.
В качестве примера, на рис. 5 приведена векторная диаграмма одного из возможных режимов работы четырёхпроводной трёхфазной цепи при несимметричном приёмнике.
Как уже говорилось при симметричном режиме в данной цепи необходимость в нейтральном проводе отпадает. В этом случае схема будет иметь вид (рис. 6) и называется трёхпроводной трёхфазной цепью “звезда – звезда без нейтрального провода”. В случае симметричного приёмника расчет данной цепи (рис. 6) проводят по соотношениям (11), (13), (15), (16), (17). Возможная векторная диаграмма аналогична рис. 4.
|
|
|
Рассмотрим несимметричные режимы работы трёхпроводной цепи (рис. 6).
Расчет таких режимов проводят методом двух узлов. Сначала определяют напряжение смещения нейтрали
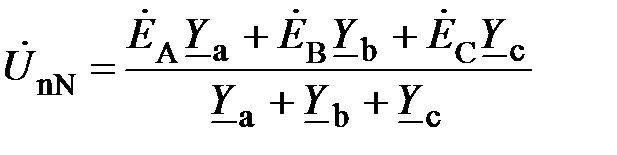 (20)
(20)
где 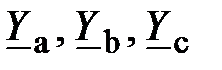 – проводимости фаз.
– проводимости фаз.
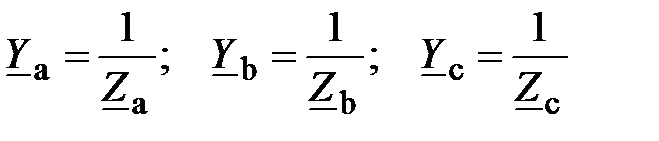 . (21)
. (21)
Согласно II закона Кирхгофа для контура AanN (рис. 6) будем иметь:
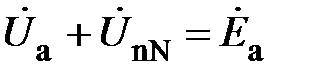
Из последнего равенства определяют фазное напряжение  :
:
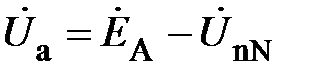
Аналогично рассматривая контуры BbnN, CcnN, получают:
 ;
;
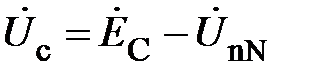 . (22)
. (22)
Наконец, рассчитывают фазные токи по соотношению (15).
В качестве примера, иллюстрирующего несимметричный режим в трёхпроводной системе, приведена векторная диаграмма напряжений рис. 7. Она показывает, что нарушение симметрии происходит только со стороны нагрузки, системы же векторов фазных ЭДС генератора (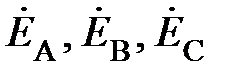 ) и, отдельно, линейных напряжений (
) и, отдельно, линейных напряжений (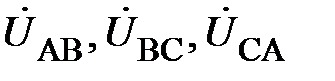 ) сохраняют свои трехфазные симметричные системы. Соотношение между линейными и фазными напряжениями (11) нарушается. При этом фазные напряжения могут значительно превышать линейные по модулю. Это возможно только в случае активно-реактивного приёмника. Поэтому питание несимметричного приёмника, включённого звездой, от трёхпроводной сети (без нейтрального провода) является недопустимым.
) сохраняют свои трехфазные симметричные системы. Соотношение между линейными и фазными напряжениями (11) нарушается. При этом фазные напряжения могут значительно превышать линейные по модулю. Это возможно только в случае активно-реактивного приёмника. Поэтому питание несимметричного приёмника, включённого звездой, от трёхпроводной сети (без нейтрального провода) является недопустимым.
Проанализируем возможные режимы работы трёхфазного приёмника с чисто активным характером нагрузки, соединённого звездой без нейтрального провода.
1. Симметричный режим характеризует векторная диаграмма на рис. 8. Здесь все три группы векторов 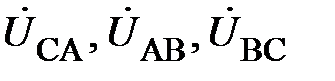 ;
;  ;
; 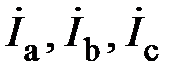 образуют каждая свою трёхфазную симметричную систему. Кроме этого, вектора
образуют каждая свою трёхфазную симметричную систему. Кроме этого, вектора 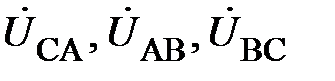 , построенные так, как показано на рис. 8, образуют равносторонний треугольник АВС, в котором точка N(n) является его центром. Если приемник симметричный, то
, построенные так, как показано на рис. 8, образуют равносторонний треугольник АВС, в котором точка N(n) является его центром. Если приемник симметричный, то 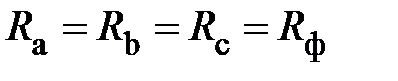 или
или 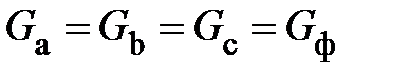 (
(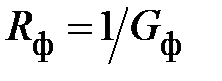 ). Из (20) получим
). Из (20) получим
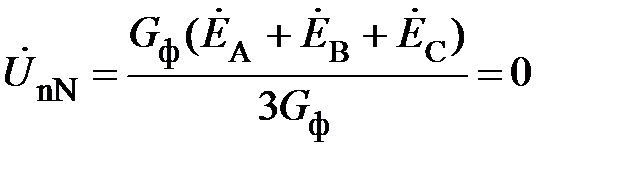 .
.
2. При обрыве одной фазы, например фазы А (рис. 9), приёмники остальных фаз оказываются включёнными последовательно под линейное напряжение  (на рис. 9 векторы фазных ЭДС не показаны). Падение напряжения на каждом приёмнике R b и R c распределяется пропорционально их сопротивлениям. Если R b= R c, то
(на рис. 9 векторы фазных ЭДС не показаны). Падение напряжения на каждом приёмнике R b и R c распределяется пропорционально их сопротивлениям. Если R b= R c, то
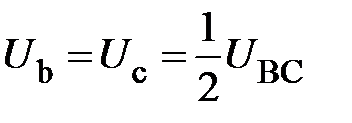 .
.
Т. е. потенциал точки n изменяется и на векторной диаграмме эта точка смещается в точку О (рис. 10). Данный вывод следует из соотношения (20) при G a=0
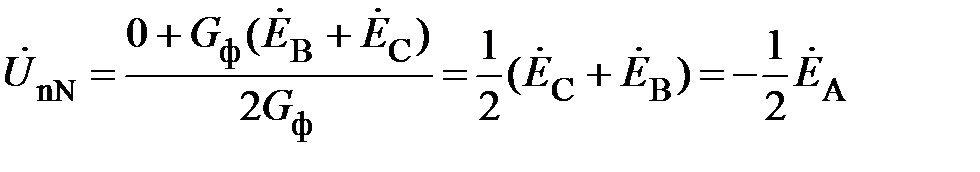 . (23)
. (23)
Т. о., фазные напряжения U bи U c уменьшаются
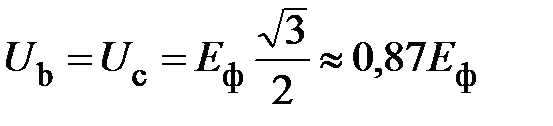 .
.
В таком же соотношении изменяются фазные и линейные токи. Фазное напряжение оборванной фазы увеличивается
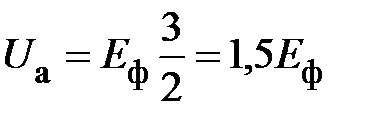 .
.
Более строго данные выводы можно определить при использовании векторных соотношений. Используя (3), (21) и (23), получим
 ;
;
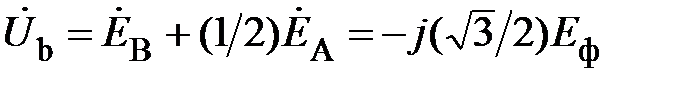 ;
;
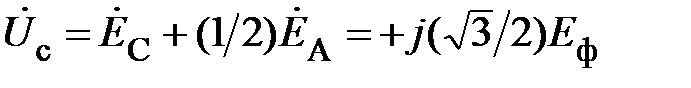 .
.
Эти соотношения полностью определяют соответствующие вектора на диаграмме рис. 10.
|
|
|
3. При коротком замыкании фазы, например, фазы А (рис. 11):
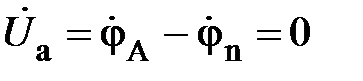 ,
,
т. е. 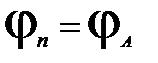 точка n принимает потенциал линейного провода А и приёмники в остальных фазах В и С оказываются включёнными под линейные напряжения, соответственно
точка n принимает потенциал линейного провода А и приёмники в остальных фазах В и С оказываются включёнными под линейные напряжения, соответственно 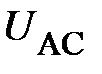 и
и 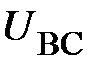 . Действительно, как следует из (20) при
. Действительно, как следует из (20) при 
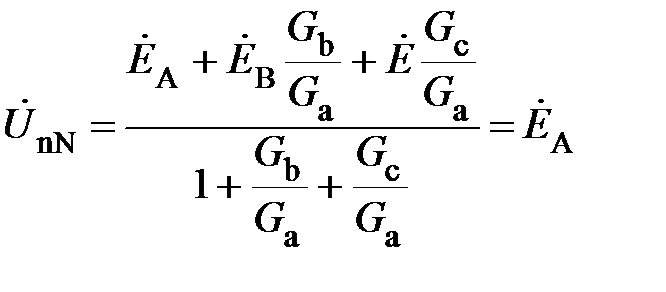 .
.
При этом, учитывая (3), (21), получим
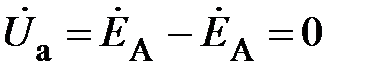 ;
;
 ;
;
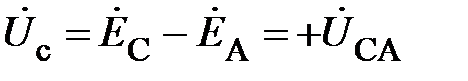 .
.
Т. е. модули фазных напряжений  и
и 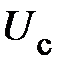 увеличиваются в
увеличиваются в 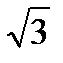 раз,
раз,
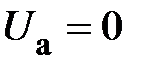 .
.
Соответственно увеличиваются и токи I b и I c. Если R b= R c, то ток в фазе А увеличится в 3 раза
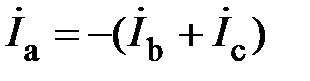 .
.
Аналогичный результат можно получить и для активно-реактивного приёмника. Если модуль полного сопротивления одной из фаз изменяется, например, 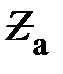 изменяется от 0 до
изменяется от 0 до 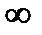 , а
, а  , то напряжения будут изменяться в следующих пределах
, то напряжения будут изменяться в следующих пределах
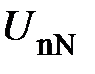 – от
– от 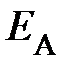 до –
до –  ;
;
 и
и 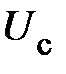 от –
от – 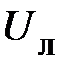 до
до 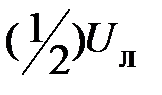 ;
;
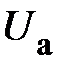 от – 0 до 1,5
от – 0 до 1,5 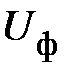 .
.
Если при этом 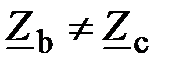 и приёмники чисто активные
и приёмники чисто активные  ;
;  ;
; 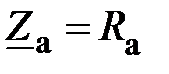 , то точка n может сместиться на векторной диаграмме в любую точку внутри треугольника ABC.
, то точка n может сместиться на векторной диаграмме в любую точку внутри треугольника ABC.
Энергетические процессы, протекающие в каждой фазе, подобны процессам в однофазной цепи и, при заданных 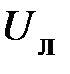 и
и  , определяются величиной и характером фазной нагрузки
, определяются величиной и характером фазной нагрузки 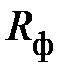 и
и 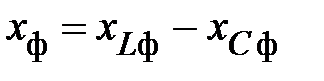 . При этом
. При этом
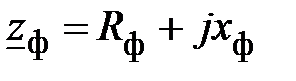 ,
,  .
.
1. Активная мощность на трехфазном приемнике равна арифметической сумме активных мощностей на каждой его фазе
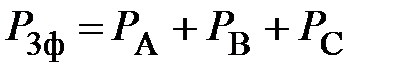 .
.
При этом активную мощность на каждой фазе приемника можно определить
 ,
,
где 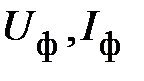 – соответственно, действующие значения фазного напряжения и тока;
– соответственно, действующие значения фазного напряжения и тока; 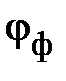 – угол сдвига фаз между синусоидами фазного напряжения и тока
– угол сдвига фаз между синусоидами фазного напряжения и тока
 .
.
Если приемник симметричный, то
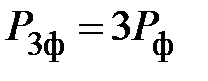 .
.
2. Реактивная мощность на трехфазном приемнике равна алгебраической сумме реактивных мощностей на каждой его фазе
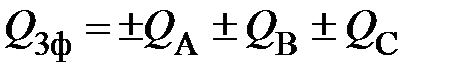
или
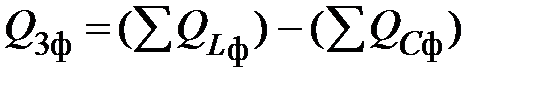 ,
,
где 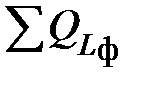 ,
, 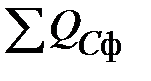 – соответственно, суммарная мощность на всех индуктивных и емкостных элементах в фазах приемника. При этом реактивную мощность на каждой фазе приемника можно определить
– соответственно, суммарная мощность на всех индуктивных и емкостных элементах в фазах приемника. При этом реактивную мощность на каждой фазе приемника можно определить
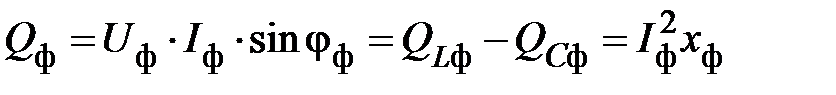 ;
;
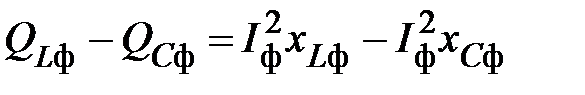 .
.
Если приемник симметричный, то
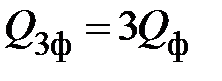 .
.
3. Наконец, полная комплексная мощность на трехфазном приемнике равна геометрической сумме полных комплексных мощностей на каждой его фазе
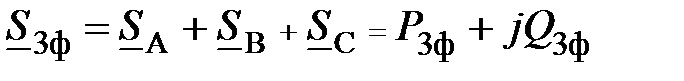 .
.
Причем полную мощность на этом приемнике можно определить так
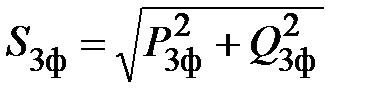 .
.
Полную комплексную мощность и полную мощность на каждой фазе приемника определяют с помощью формул
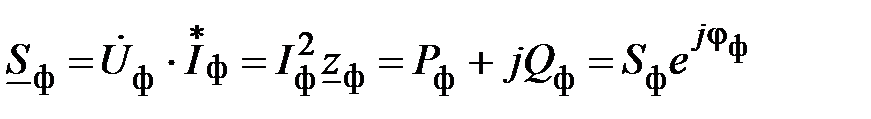 ;
;
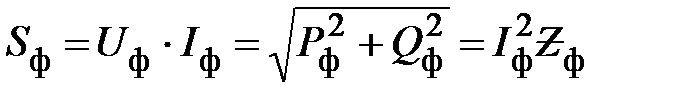 .
.
Если приемник симметричный, то
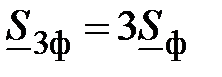
и
 .
.
Основные выводы
1. Для уменьшения числа соединительных проводов в трехфазной цепи используют один из возможных способов соединения фаз приёмника между собой: соединение звездой.
2. При этом возможно использование четырехпроводной цепи (с нейтральным проводом), которую используют для питания несимметричного приёмника. Для такой цепи справедливы соотношения
 ;
; 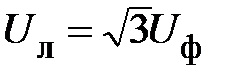 . (24)
. (24)
Наличие нейтрального провода позволяет сохранить симметрию фазных напряжений, поэтому в этом проводе недопустима установка предохранителей.
3. Использование трехпроводной трёхфазной сети рекомендуется исключительно при питании симметричных приёмников. В этом случае остаются справедливыми соотношения (24). Для несимметричного приёмника в этом случае фазные напряжения могут значительно превысить свои номинальные значения 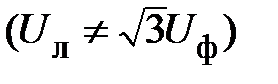 , что может привести к выходу из строя приёмников.
, что может привести к выходу из строя приёмников.
Порядок выполнения работы
1. По указанию преподавателя собрать одну из схем для исследования трёхфазной цепи при соединении приёмников в звезду без нейтрального провода (рис.12):
· с активным трёхфазным приёмником. В качестве приёмника используется ламповый реостат, в котором в каждой фазе несколько ламп накаливания включены параллельно и предусмотрена возможность их поочерёдного включения – выключения;
· с активно-индуктивным или активно-ёмкостным трёхфазным приёмником. В данном приёмнике предусмотрена возможность включения – выключения в каждой фазе дополнительного резистора, соединённого последовательно с катушкой индуктивности или с конденсатором.
2. Исследовать следующие режимы работы:
· симметричный режим работы. В каждой фазе со стороны нагрузки должно быть включено одинаковое число ламп, если приёмник активный. Для реактивного приёмника дополнительные резисторы должны быть выключены;
· несимметричный режим работы. Для активного приёмника выключить в одной фазе две лампы, в другой – одну, в третьей оставить включенными все лампы. Для реактивного приёмника включить в двух фазах дополнительные резисторы;
· режим работы при обрыве фазы. Для активного приёмника выключить все лампы в одной фазе. При этом в остальных двух фазах все лампы должны быть включены. Для реактивного приёмника выключить полностью нагрузку в одной фазе;
· режим работы при коротком замыкании фазы. Для любого приёмника восстановить симметричную нагрузку по фазам. При отключенном трехфазном источнике питания соединить проводником начало одной из фаз приемника с нейтральной точкой 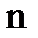 . Подключить источник и исследовать режим;
. Подключить источник и исследовать режим;
· показания приборов при исследовании каждого указанного режима записать в таблицу 1.
3. По результатам исследований построить векторные диаграммы напряжений и токов во всех фазах приемника. Для одной из фаз активно-реактивного приемника построить векторную диаграмму сопротивлений, используя формулы
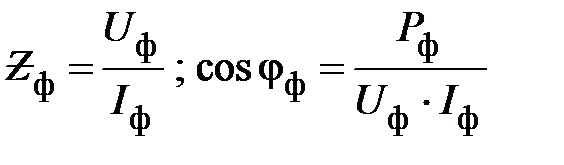 ;
;
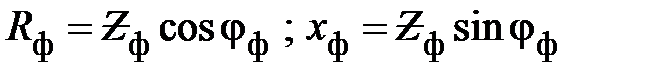 .
.
Знак угла сдвига фаз между 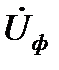 и
и 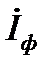 определяется характером нагрузки. При этом для активного приёмника
определяется характером нагрузки. При этом для активного приёмника 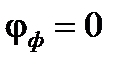 , для активно-индуктивного приёмника
, для активно-индуктивного приёмника 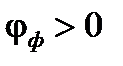 , для активно-емкостного приёмника
, для активно-емкостного приёмника  .
.
Также определить полную, активную и реактивную мощность на трехфазном приемнике и на каждой его фазе с помощью указанных выше формул (для активно-реактивного приемника). Для одной из фаз приемника построить векторную диаграмму мощностей.
4. Собрать схему для исследования трёхфазной цепи при соединении приёмников в звезду с нейтральным проводом. При этом по указанию преподавателя использовать либо активный приёмник, либо активно-реактивный приёмник (рис.13).
5. Исследовать следующее режимы работы:
· симметричный режим работы;
· несимметричный режим работы;
· режим работы при обрыве фазы.
6. Результаты измерений занести в таблицу 2.
Примечание. Режим короткого замыкания фазы при наличии нейтрального провода проводить нельзя. В этом случае произойдет замыкание фазы источника с помощью линейного и нейтрального проводов, имеющих очень малые сопротивления. При этом ток в этих проводах
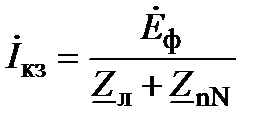
может в десятки раз превышать номинальный, что вызовет выход из строя стендового источника питания, амперметров и ваттметров.
7. По данным измерений построить векторные диаграммы напряжений и токов для исследованных режимов работы трёхфазной цепи во всех фазах приемника и в нейтральном проводе. При этом графически определить величину и начальную фазу 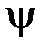 тока в нулевом проводе. Для реактивного приёмника определить полные, активные и реактивные мощности на каждой фазе и в целом на приемнике. Построить векторную диаграмму мощностей для одной из его фаз.
тока в нулевом проводе. Для реактивного приёмника определить полные, активные и реактивные мощности на каждой фазе и в целом на приемнике. Построить векторную диаграмму мощностей для одной из его фаз.
Рекомендуемая литература
1. Касаткин А.С., Немцов М.В. Электротехника: Учебн. пособ. для ВУЗов. М.: Издательский центр «Академия», 2005 (подразделы 3.1, 3.2, 3.4, 3.6, 3.8).
2. Электротехника: Учебник для неэлектрических специальностей ВУЗов / Под ред. В.Г. Герасимова. М.: Высшая школа, 1985 (подразделы 3.4, 3.5, 3.7, 3.8, 3.10).
3. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника: Учебник для ВУЗов. М.: Энергоатомиздат, 1985 (подразделы 3.1, 3.2, 3.3, 3.4, 3.8).
4. Общая электротехника: Учебн. пособие для ВУЗов / Под ред. Блажкина А.Т. Л.: Энергоатомиздат, 1986 (подразделы 4.1, 4.2, 4.3, 4.4).
Контрольные вопросы
1. Дать определение трёхфазной цепи и симметричной трёхфазной системы ЭДС.
2. Написать выражение для мгновенных значений и для комплексов действующих значений симметричной трёхфазной системы ЭДС.
3. Как получить соединение фаз приёмника звездой?
4. Какие напряжения в трёхфазной цепи называются фазными и линейными? Определить эти напряжения на схеме.
5. Какие существуют соотношения между линейными и фазными токами и напряжениями? Обосновать справедливость этих соотношений.
6. Написать выражения мощности для цепи трёхфазного тока при симметричной и несимметричной нагрузке.
7. Заданы параметры схемы замещения трёхфазной цепи (рис.3)
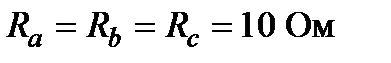 ;
;  ;
;  ;
; 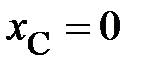 ;
; 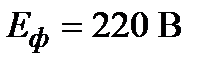 .
.
Определить:
·  ;
;
· 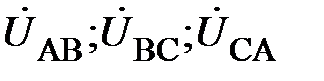 ;
;
· 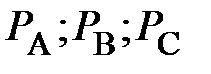 ;
;
8. Для трёхфазной цепи (рис.9) известны сопротивления фаз приёмника 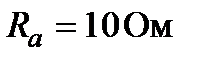 ;
; 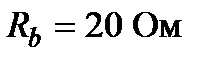 ;
;  ;
; 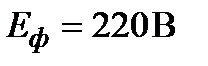 .
.
9. Определить:
· 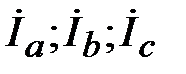
· 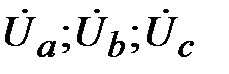
и построить соответствующую векторную диаграмму токов или напряжений.
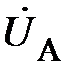
|
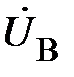
|

|

|
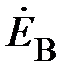
|
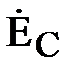
|
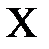
|

|

|
|

|
|
Рис. 1.
|
|
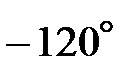
|
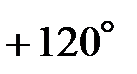
|
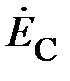
|
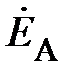
|
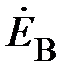
|
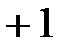
|
Рис. 2.
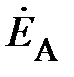
|
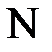
|
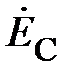
|

|

|
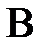
|

|
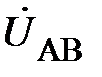
|
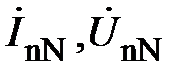
|
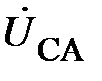
|
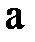
|
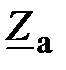
|
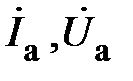
|
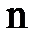
|
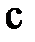
|
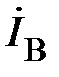
|
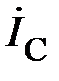
|
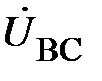
|
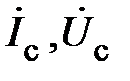
|
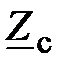
|
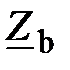
|
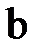
|

|
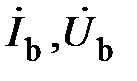
|
Рис. 3.
 |  |

|
|
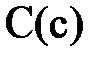
|
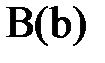
|
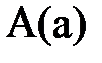
|
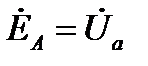
|
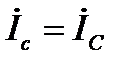
|
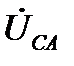
|
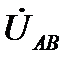
|
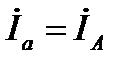
|
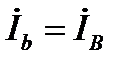
|
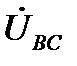
|
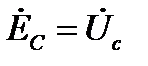
|

|
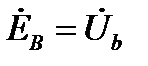
|
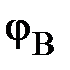
|
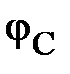
|
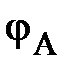
|

|

|

|
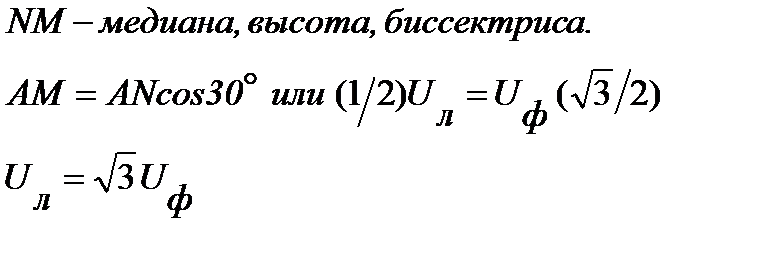
|
Рис. 4.
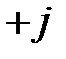
|
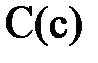
|
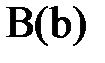
|
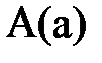
|
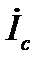
|
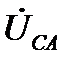
|
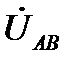
|
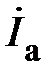
|
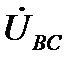
|
|
|
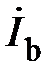
|
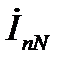
|
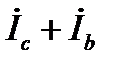
|
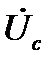
|
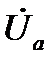
|

|
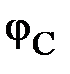
|
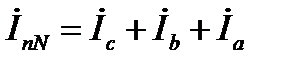
|
| +1 |
Рис. 5.
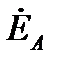
|
|
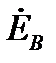
|
|
|

|
|
|
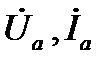
|
|

|

|

|

|
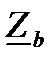
|
|
|
|
|
|
|
|
|
|
Рис. 6.
|
|
|


