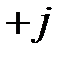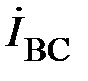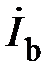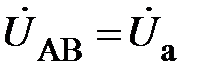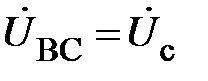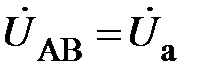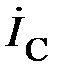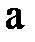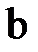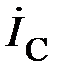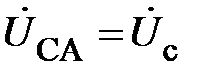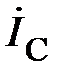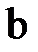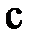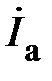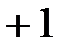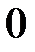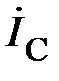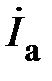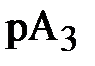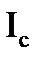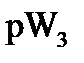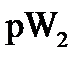Основные теоретические положения
Помимо соединения фаз приёмника или генератора в звезду их можно соединить треугольником. При соединении фаз генератора или приёмника по схеме треугольник, конец предыдущей фазы, начиная с фазы А, соединяется с началом последующей фазы В, конец фазы В – с началом фазы С и, наконец, конец фазы С – с началом фазы А (рис.1). Объединённые концы фаз трёхфазного приёмника или генератора соединяют с линейными проводами. Соединенные таким образом фазы образуют замкнутый контур, который принято на схемах изображать, как показано на рис.2.
Как правило, фазы генератора соединяют по схеме звезда. Поэтому наиболее вероятной является трёхфазная цепь, в которой приёмник соединён треугольником, приведена на рис.3. При таком соединении приёмника каждая его фаза подключается непосредственно к линейному напряжению. Поэтому при соединении приёмника по схеме треугольник соотношения
 (1)
(1)
или

справедливо для симметричного и несимметричного приёмника. Будем, как и в работе №7, считать трехфазную цепь «короткой», то есть величиной сопротивления линейных проводов пренебрегаем
 . (2)
. (2)
Отсюда следует
 .
.
То есть линейные напряжения  не зависят от расстояния вдоль линейных проводов и обеспечиваются фазными ЭДС генератора. Поскольку считаем, что фазные ЭДС генератора всегда образуют трехфазную симметричную систему, то этому же условию всегда будут удовлетворять и линейные напряжения (независимо от режима работы трехфазной цепи)
не зависят от расстояния вдоль линейных проводов и обеспечиваются фазными ЭДС генератора. Поскольку считаем, что фазные ЭДС генератора всегда образуют трехфазную симметричную систему, то этому же условию всегда будут удовлетворять и линейные напряжения (независимо от режима работы трехфазной цепи)
Рассмотрим связь между линейными и фазными токами. Фазные токи  ,
,  ,
,  текут в фазах приёмника; линейные токи
текут в фазах приёмника; линейные токи  ,
,  ,
,  – в линейных проводах. По 1-ому закону Кирхгофа для узла а запишем (рис. 3):
– в линейных проводах. По 1-ому закону Кирхгофа для узла а запишем (рис. 3):

или (рис. 4)
 (3)
(3)
Рассматривая аналогично уравнения, составленные для узлов b и c, получим
 (4)
(4)
Т.е. в самом общем случае комплексный вектор линейного тока равен разности комплексных векторов соответствующих фазных токов. Причём соотношения (3) и (4) не зависит от того, является ли нагрузка приёмника симметричной или несимметричной.
Если нагрузка симметричная, то вектора фазных и линейных токов образуют на векторной диаграмме трёхфазную симметричную систему (рис.4). При этом сдвиг фаз между синусоидами фазного напряжения и тока одинаковы для всех фаз приемника
 .
.
Аналогично для сдвига фаз между синусоидами линейного напряжения и тока
 .
.
Рассмотрим треугольник, составленный из векторов  (рис. 4). Он является равнобедренным с углами при основании треугольника
(рис. 4). Он является равнобедренным с углами при основании треугольника  . Поэтому действующие значения фазного и линейного токов связаны соотношением
. Поэтому действующие значения фазного и линейного токов связаны соотношением
 , (5)
, (5)
которое является справедливым только для симметричного приёмника.
Энергетические процессы, протекающие в трёхфазном приёмнике, соединённом по схеме звезда или треугольник, подобны. При этом активная мощность приёмника
 (6)
(6)
равна арифметической сумме активных мощностей каждой фазы. Активная мощность в каждой фазе определяется
 , (7)
, (7)
если приёмник симметричный, то
 , (8)
, (8)
и
 . (9)
. (9)
Реактивная мощность приёмника
 (10)
(10)
равна алгебраической сумме реактивных мощностей каждой фазы.
Реактивная мощность каждой фазы определяется по формулам
 , (11)
, (11)
если приёмник симметричный, то
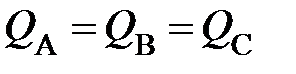 , (12)
, (12)
и
 . (13)
. (13)
Полная комплексная мощность приёмника
 (14)
(14)
определяется суммой полных комплексных мощностей каждой фазы. Модуль полной мощности приёмника равен
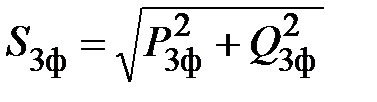 , (15)
, (15)
а модуль полной мощности каждой фазы:
 . (16)
. (16)
Если приёмник симметричный, то
 (17)
(17)
Расчёт трёхфазной цепи с приёмником, соединённым треугольником, начинают с определения фазных токов
 ;
;  ;
;  . (19)
. (19)
Затем определяют линейные токи по соотношениям (3) и (4). После чего рассчитывают мощности приёмника и фаз по соотношениям (7) – (17).
Если приёмник симметричный, то для определения фазных токов достаточно вычислить ток 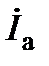 по соотношению (18); остальные токи (
по соотношению (18); остальные токи (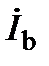 и
и  ) будут равны ему по модулю и их углы сдвига фаз, соответственно,
) будут равны ему по модулю и их углы сдвига фаз, соответственно,  и
и  , равны
, равны  . Начальные фазы синусоид фазных токов (или начальные фазы векторов
. Начальные фазы синусоид фазных токов (или начальные фазы векторов  и
и  ) можно определить, зная, что
) можно определить, зная, что
 ;
;
 ;
;
 .
.
Модуль линейного тока  равен
равен
 .
.
Такое же соотношение будут иметь модули линейных и фазных токов  и
и  ,
,  и
и  . При этом синусоиды линейных токов будут иметь следующие начальные фазы (или начальные фазы векторов линейных токов)
. При этом синусоиды линейных токов будут иметь следующие начальные фазы (или начальные фазы векторов линейных токов)
 ;
;
 ;
;
 .
.
Мощность каждой фазы и всего приемника рассчитывают по формулам (8), (9), (12), (13) и (16), (17).
Весьма часто в экспериментах известны  и характер нагрузки каждой фазы, нам необходимо по этим данным построить векторную диаграмму. Сначала определяют активные сопротивления каждой фазы
и характер нагрузки каждой фазы, нам необходимо по этим данным построить векторную диаграмму. Сначала определяют активные сопротивления каждой фазы
 , (19)
, (19)
затем полные сопротивления каждой фазы
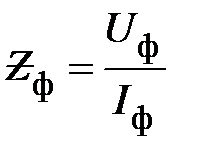 (20)
(20)
и реактивные сопротивления каждой фазы
 , (21)
, (21)
где “+” соответствует активно-индуктивному характеру нагрузки фазы, а “-” – активно-ёмкостному характеру нагрузки фазы.
Затем определяют углы сдвига фаз между  и
и 
 . (22)
. (22)
После чего по соотношениям (3) и (4) определяют линейные токи. Наконец, по соотношениям (9), (11), (13), (15),(16) рассчитывают мощности фаз и мощности всего трехфазного приёмника.
Построение векторной диаграммы на комплексной плоскости (рис.5) начинают с выбора масштабов  и
и  . После чего:
. После чего:
– вектор  в масштабе
в масштабе  размещают вдоль оси +1;
размещают вдоль оси +1;
– строят вектора  и
и  , зная их начальные фазы
, зная их начальные фазы
 ;
;  ;
;
– в соответствии со знаками и величиной углов сдвига фаз  определяют направления и строят в масштабе
определяют направления и строят в масштабе  вектора
вектора  ;
;
– графическим способом (как векторная разность) определяют  ,
,  согласно соотношениям (3) и (4);
согласно соотношениям (3) и (4);
– наконец, строят треугольники мощностей  , используя их рассчитанные значения.
, используя их рассчитанные значения.
Приведённая в качестве примера векторная диаграмма является одной из возможных (рис. 5).
В заключении проанализируем некоторые режимы приёмника:
1. Симметричный режим работы приемника. Для приёмника с активно-реактивным характером нагрузки (при условии, что  ) симметричный режим уже рассмотрен выше и векторная диаграмма приведена на рис.4.
) симметричный режим уже рассмотрен выше и векторная диаграмма приведена на рис.4.
В случае чисто активного приёмника сдвиг фаз между синусоидами фазного напряжения и тока  , следовательно, соответствующие вектора фазных (или линейных) напряжений и фазных токов совпадают по направлению. Вектора
, следовательно, соответствующие вектора фазных (или линейных) напряжений и фазных токов совпадают по направлению. Вектора 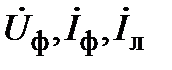 образуют три трёхфазных симметричных системы (рис.6).
образуют три трёхфазных симметричных системы (рис.6).
2. Несимметричный режим работы приемника. Для приёмника с активно-реактивным характером нагрузки данный режим рассмотрен выше. Возможная векторная диаграмма приведена на рис.5. Для приёмника с активным характером нагрузки возможная векторная диаграмма такого режима при уменьшении нагрузки в фазе А ( ) приведена на рис.7. На ней ток
) приведена на рис.7. На ней ток 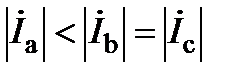 . Её построение проводят так же как и для симметричного режима работы.
. Её построение проводят так же как и для симметричного режима работы.
3. Режим работы приёмника при обрыве одной из его фаз. При обрыве одной из фаз симметричного приёмника, например, фазы А, ток  (рис.8). Линейные (одновременно это фазные) напряжения сохраняют свою симметрию. Токи
(рис.8). Линейные (одновременно это фазные) напряжения сохраняют свою симметрию. Токи  и
и 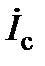 не изменяют своего значения, поскольку
не изменяют своего значения, поскольку  и
и  не изменяются. Линейные токи становятся равными
не изменяются. Линейные токи становятся равными
 ;
;
 ;
;
 .
.
Качественная векторная диаграмма для активного приемника полностью соответствует приведенной на рис. 9. Векторная диаграмма для активно-реактивного  приёмника, приведенная на рис.10, также соответствует рассматриваемому режиму, но является одной из возможных.
приёмника, приведенная на рис.10, также соответствует рассматриваемому режиму, но является одной из возможных.
4. Режим работы приемника при обрыве линейного провода. При обрыве линейного провода, например, провода фазы А, получим схему, приведённую на рис.11. Трёхфазный симметричный приёмник становится обычной однофазной цепью, включенной под напряжение  . Образованная фазами приёмника цепь имеет смешанный характер соединения и состоит из двух параллельных ветвей: ветви
. Образованная фазами приёмника цепь имеет смешанный характер соединения и состоит из двух параллельных ветвей: ветви  , в которой нагрузка фаз приемника
, в которой нагрузка фаз приемника  и
и  включена последовательно, и ветви
включена последовательно, и ветви  с нагрузкой
с нагрузкой  .
.
Поскольку нагрузки фаз  и
и  включены последовательно и приёмник – симметричный, то фазные напряжения в этих фазах становятся равными (с учётом выбранных положительных обозначений) следующему значению
включены последовательно и приёмник – симметричный, то фазные напряжения в этих фазах становятся равными (с учётом выбранных положительных обозначений) следующему значению
 ,
,
т.е. уменьшаются в 2 раза по модулю по сравнению с симметричным режимом работы приемника. Фазный ток  сохраняет свою величину, поскольку величина
сохраняет свою величину, поскольку величина  не изменяется
не изменяется
 .
.
В то же время фазные токи  уменьшаются в два раза пропорционально уменьшению фазных напряжений
уменьшаются в два раза пропорционально уменьшению фазных напряжений
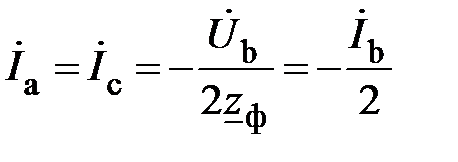 .
.
Линейные токи определяются по соотношениям (3) и (4)
 ;
;
 ;
;
 .
.
Т.е. линейные токи  и
и  в любой момент времени противоположны по направлению.
в любой момент времени противоположны по направлению.
Упрощённая векторная диаграмма для активно-реактивного  приёмника приведена на рис.12. Для активного приёмника все вектора токов и напряжений располагаются вдоль прямых, параллельных вектору
приёмника приведена на рис.12. Для активного приёмника все вектора токов и напряжений располагаются вдоль прямых, параллельных вектору  т. к.
т. к. 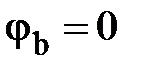 .
.
ВЫВОДЫ
1. Соединение трёхфазного приёмника по схеме треугольник не столь критично к влиянию неравномерности нагрузки фаз (в том числе при обрыве одной из фаз или линейного провода) на режим работы приемника. Это связано с тем, что при выполнении условия (2) фазные напряжения сохраняют свою симметрию и равенство соответствующим линейным напряжениям. Кроме этого они обеспечиваются симметричными фазными ЭДС генератора.
2. В то же время соединение фаз приемника по схеме треугольник допустимо не для всех приёмников, так как фазное напряжение в этом случае увеличивается в  по сравнению с фазным напряжением симметричного приемника, соединенного по схеме звезда. Одновременно увеличивается во столько же раз фазный ток. При этом в 3 раза возрастает мощность и тепловые потери приемника.
по сравнению с фазным напряжением симметричного приемника, соединенного по схеме звезда. Одновременно увеличивается во столько же раз фазный ток. При этом в 3 раза возрастает мощность и тепловые потери приемника.
3. Для такой схемы соединения независимо от характера нагрузки по фазам справедливо 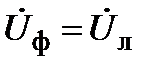 .
.
4. Для симметричного приёмника связь между модулями линейных и фазных токов выражается соотношением  .
.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Ознакомиться с приборами, необходимыми для выполнения работы.
2. В случае активно-реактивного приёмника собрать схему, указную на рис.13, в случае активного приёмника – схему на рис.14.
3. Исследовать следующие режимы работы приёмника:
1. Симметричный режим. В случае активного приёмника (ламповый реостат) должны быть включены все лампы в каждой фазе. В случае активно-реактивного приемника дополнительные резисторы зашунтированы;
2. Несимметричный режим. В случае активного приемника в одной фазе выключить две лампы, в другой – одну, в третьей фазе оставить все лампы включенными. В случае активно-реактивного приёмника в двух фазах включить в цепь дополнительные резисторы;
3. Обрыв фазы. Предварительно восстановить симметрию фаз приёмника. В случае активного приёмника выключить все лампы в одной из его фаз. В остальных фазах все лампы включить. В случае активно-реактивного приёмника отключит нагрузку одной из фаз;
4. Обрыв линейного провода. Восстановить симметрию фаз приёмника, после чего отключить один из линейных проводов от источника питания;
5. Фазные напряжения измерять переносным вольтметром (на схемах он не указан);
6. Показания приборов занести в таблицу 1 в случае активного приёмника и табл. 2 для активно-реактивного приёмника;
7. В соответствии с данными измерений (активный приемник) и результатами расчёта (активно-реактивный приёмник) построить векторные диаграммы, треугольники мощностей (по указанию преподавателя).
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Касаткин А.С., Немцов М.В. Электротехника: Учебное пособие для ВУЗов. М.: Издательский центр «Академия», 2005 (подразделы 3.3, 3.8).
2. Борисов Ю.М., Липатов Д.Н., Зорин Ю.Н. Электротехника. Учебник для ВУЗов. М.: Энергоатомиздат, 1985 (подразделы 3.5, 3.6).
3. Электротехника: Учебник для неэлектрических спец. ВУЗов / Под ред. В.Г.Герасимова. М.: Высшая школа, 1985 (подразделы 3.6 – 3.9).
4. Общая электротехника: Учебное пособие для ВУЗов / Под ред. А.Б.Блажкина. Л.: Энергоатомиздат, 1986 (подразделы 4.2, 4.3).
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Соединение фаз приёмника треугольником. Дать определение и нарисовать схему соединения фаз.
2. Соотношения между фазными и линейными параметрами режима работы приёмника.
3. Мощность в трёхфазной цепи. Определение P, Q, S.
4. По указанию преподавателя объяснить расчёт параметров и построение векторной диаграммы.
Рис. 1.
Рис. 2.

 Рис. 3.
Рис. 3.

 Рис. 4.
Рис. 4.
Рис. 5.
Рис. 6.
Рис. 7.
Рис. 8.
Рис. 9.
Рис. 10.
Рис. 11.
Рис. 12.

Воспользуйтесь поиском по сайту:


 (1)
(1)
 . (2)
. (2) .
. не зависят от расстояния вдоль линейных проводов и обеспечиваются фазными ЭДС генератора. Поскольку считаем, что фазные ЭДС генератора всегда образуют трехфазную симметричную систему, то этому же условию всегда будут удовлетворять и линейные напряжения (независимо от режима работы трехфазной цепи)
не зависят от расстояния вдоль линейных проводов и обеспечиваются фазными ЭДС генератора. Поскольку считаем, что фазные ЭДС генератора всегда образуют трехфазную симметричную систему, то этому же условию всегда будут удовлетворять и линейные напряжения (независимо от режима работы трехфазной цепи) ,
,  ,
,  текут в фазах приёмника; линейные токи
текут в фазах приёмника; линейные токи  ,
,  ,
,  – в линейных проводах. По 1-ому закону Кирхгофа для узла а запишем (рис. 3):
– в линейных проводах. По 1-ому закону Кирхгофа для узла а запишем (рис. 3):
 (3)
(3) (4)
(4) .
. .
. (рис. 4). Он является равнобедренным с углами при основании треугольника
(рис. 4). Он является равнобедренным с углами при основании треугольника  . Поэтому действующие значения фазного и линейного токов связаны соотношением
. Поэтому действующие значения фазного и линейного токов связаны соотношением , (5)
, (5) (6)
(6) , (7)
, (7) , (8)
, (8) . (9)
. (9) (10)
(10) , (11)
, (11)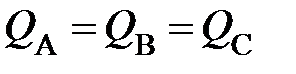 , (12)
, (12) . (13)
. (13) (14)
(14)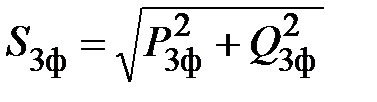 , (15)
, (15) . (16)
. (16) (17)
(17) ;
;  ;
;  . (19)
. (19)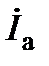 по соотношению (18); остальные токи (
по соотношению (18); остальные токи (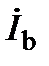 и
и  ) будут равны ему по модулю и их углы сдвига фаз, соответственно,
) будут равны ему по модулю и их углы сдвига фаз, соответственно,  и
и  , равны
, равны  . Начальные фазы синусоид фазных токов (или начальные фазы векторов
. Начальные фазы синусоид фазных токов (или начальные фазы векторов  и
и  ) можно определить, зная, что
) можно определить, зная, что ;
; ;
; .
. равен
равен .
. и
и  ,
,  и
и  . При этом синусоиды линейных токов будут иметь следующие начальные фазы (или начальные фазы векторов линейных токов)
. При этом синусоиды линейных токов будут иметь следующие начальные фазы (или начальные фазы векторов линейных токов) ;
; ;
; .
. и характер нагрузки каждой фазы, нам необходимо по этим данным построить векторную диаграмму. Сначала определяют активные сопротивления каждой фазы
и характер нагрузки каждой фазы, нам необходимо по этим данным построить векторную диаграмму. Сначала определяют активные сопротивления каждой фазы , (19)
, (19)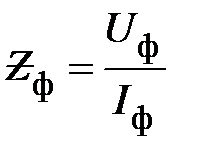 (20)
(20) , (21)
, (21) и
и 
 . (22)
. (22) и
и  . После чего:
. После чего: в масштабе
в масштабе  размещают вдоль оси +1;
размещают вдоль оси +1; и
и  , зная их начальные фазы
, зная их начальные фазы ;
;  ;
; определяют направления и строят в масштабе
определяют направления и строят в масштабе  вектора
вектора  ;
; ,
,  согласно соотношениям (3) и (4);
согласно соотношениям (3) и (4); , используя их рассчитанные значения.
, используя их рассчитанные значения. ) симметричный режим уже рассмотрен выше и векторная диаграмма приведена на рис.4.
) симметричный режим уже рассмотрен выше и векторная диаграмма приведена на рис.4. , следовательно, соответствующие вектора фазных (или линейных) напряжений и фазных токов совпадают по направлению. Вектора
, следовательно, соответствующие вектора фазных (или линейных) напряжений и фазных токов совпадают по направлению. Вектора 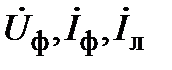 образуют три трёхфазных симметричных системы (рис.6).
образуют три трёхфазных симметричных системы (рис.6). ) приведена на рис.7. На ней ток
) приведена на рис.7. На ней ток 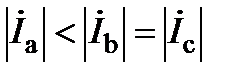 . Её построение проводят так же как и для симметричного режима работы.
. Её построение проводят так же как и для симметричного режима работы. (рис.8). Линейные (одновременно это фазные) напряжения сохраняют свою симметрию. Токи
(рис.8). Линейные (одновременно это фазные) напряжения сохраняют свою симметрию. Токи  и
и 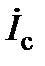 не изменяют своего значения, поскольку
не изменяют своего значения, поскольку  и
и  не изменяются. Линейные токи становятся равными
не изменяются. Линейные токи становятся равными ;
; ;
; .
. приёмника, приведенная на рис.10, также соответствует рассматриваемому режиму, но является одной из возможных.
приёмника, приведенная на рис.10, также соответствует рассматриваемому режиму, но является одной из возможных. . Образованная фазами приёмника цепь имеет смешанный характер соединения и состоит из двух параллельных ветвей: ветви
. Образованная фазами приёмника цепь имеет смешанный характер соединения и состоит из двух параллельных ветвей: ветви  , в которой нагрузка фаз приемника
, в которой нагрузка фаз приемника  и
и  включена последовательно, и ветви
включена последовательно, и ветви  с нагрузкой
с нагрузкой  .
. и
и  включены последовательно и приёмник – симметричный, то фазные напряжения в этих фазах становятся равными (с учётом выбранных положительных обозначений) следующему значению
включены последовательно и приёмник – симметричный, то фазные напряжения в этих фазах становятся равными (с учётом выбранных положительных обозначений) следующему значению ,
, сохраняет свою величину, поскольку величина
сохраняет свою величину, поскольку величина  не изменяется
не изменяется .
. уменьшаются в два раза пропорционально уменьшению фазных напряжений
уменьшаются в два раза пропорционально уменьшению фазных напряжений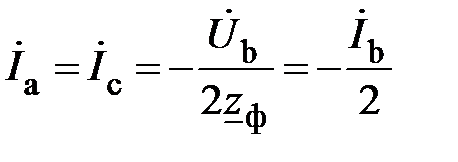 .
. ;
; ;
; .
. и
и  в любой момент времени противоположны по направлению.
в любой момент времени противоположны по направлению. приёмника приведена на рис.12. Для активного приёмника все вектора токов и напряжений располагаются вдоль прямых, параллельных вектору
приёмника приведена на рис.12. Для активного приёмника все вектора токов и напряжений располагаются вдоль прямых, параллельных вектору  т. к.
т. к. 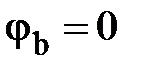 .
. по сравнению с фазным напряжением симметричного приемника, соединенного по схеме звезда. Одновременно увеличивается во столько же раз фазный ток. При этом в 3 раза возрастает мощность и тепловые потери приемника.
по сравнению с фазным напряжением симметричного приемника, соединенного по схеме звезда. Одновременно увеличивается во столько же раз фазный ток. При этом в 3 раза возрастает мощность и тепловые потери приемника.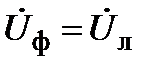 .
. .
.






































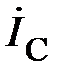





 Рис. 3.
Рис. 3.









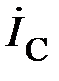










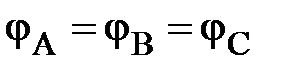







 Рис. 4.
Рис. 4.