 |
Основные теоретические положения
|
|
|
|
Рассмотрим возможную схему замещения при параллельном соединении указанных приёмников (рис.1). Используем символический метод расчета. Согласно 1 закону Кирхгофа для узла а можно записать
 , (1)
, (1)
где 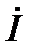 – ток в неразветвлённой части схемы или входной ток (на самом деле это комплекс действующего значения синусоидального входного тока. В целях краткого изложения материала такие величины будем называть ток, напряжение и тому подобное);
– ток в неразветвлённой части схемы или входной ток (на самом деле это комплекс действующего значения синусоидального входного тока. В целях краткого изложения материала такие величины будем называть ток, напряжение и тому подобное);  и
и  – соответственно, токи в ветвях схемы. Выразим слагаемые уравнения (1) через напряжение
– соответственно, токи в ветвях схемы. Выразим слагаемые уравнения (1) через напряжение 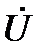 , воспользовавшись законом Ома
, воспользовавшись законом Ома
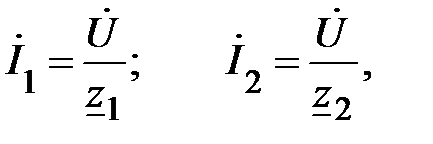 (2)
(2)
где  – комплексное сопротивление первой ветви;
– комплексное сопротивление первой ветви; 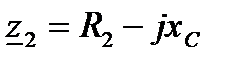 – комплексное сопротивление второй ветви. Тогда
– комплексное сопротивление второй ветви. Тогда
 . (3)
. (3)
В разделе «Основные понятия о цепях синусоидального тока» отмечено, что величина  называется комплексной проводимостью. В данном случае эту величину можно обозначить как комплексную проводимость всей цепи. Из (3) получим
называется комплексной проводимостью. В данном случае эту величину можно обозначить как комплексную проводимость всей цепи. Из (3) получим
 , (4)
, (4)
где 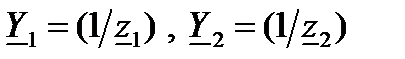 – соответственно комплексная проводимость первой и второй ветви. Таким образом, при параллельном соединении ветвей эквивалентная комплексная проводимость всей схемы замещения равна сумме комплексных проводимостей ветвей.
– соответственно комплексная проводимость первой и второй ветви. Таким образом, при параллельном соединении ветвей эквивалентная комплексная проводимость всей схемы замещения равна сумме комплексных проводимостей ветвей.
Определим составляющие комплексных проводимостей каждой ветви. Отметим, что соотношения

справедливы только для всей ветви и не могут применяться в отношении отдельных её элементов. Рассмотрим составляющие комплексных проводимостей каждой ветви.
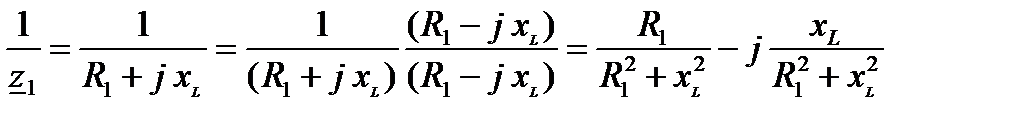 , (5)
, (5)
где 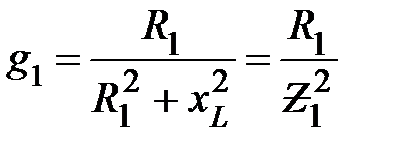 – активная составляющая проводимости первой ветви;
– активная составляющая проводимости первой ветви;  – реактивная составляющая проводимости первой ветви.
– реактивная составляющая проводимости первой ветви.
С учётом полученных соотношений
 . (6)
. (6)
|
|
|
Рассуждая аналогично, для второй ветви, получим
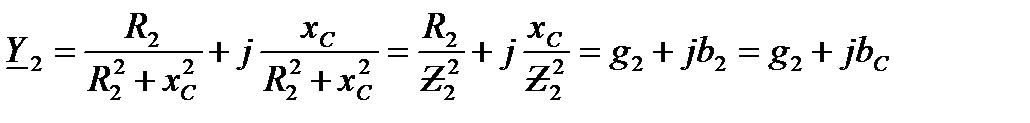 . (7)
. (7)
Тогда
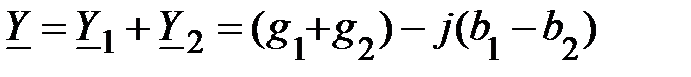 . (8)
. (8)
Положим, что синусоидальное напряжение на зажимах цепи определено выражением 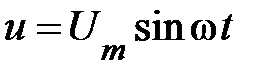 . В этом случае начальная фаза
. В этом случае начальная фаза  .
.
Комплексную проводимость всей схемы и отдельной ветви можно представить в показательной форме записи

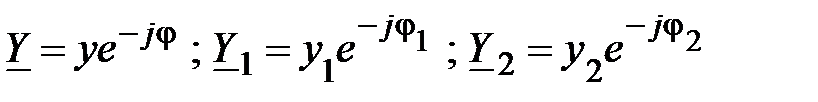 , (9)
, (9)
где 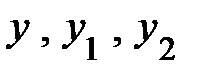 – соответственно, полная проводимость всей схемы, первой и второй ветви;
– соответственно, полная проводимость всей схемы, первой и второй ветви;  – фазовые углы указанных полных проводимостей. Они противоположны по знаку углам
– фазовые углы указанных полных проводимостей. Они противоположны по знаку углам 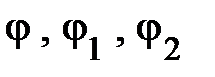 , определяющим сдвиг фаз между напряжением
, определяющим сдвиг фаз между напряжением  и, соответственно, током
и, соответственно, током  . При этом
. При этом

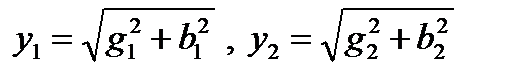 ; (10)
; (10)
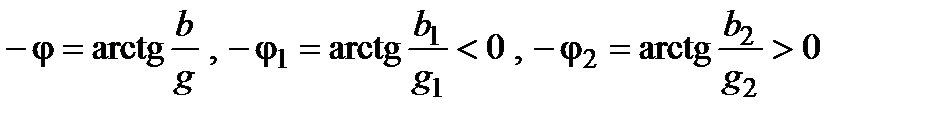 . (11)
. (11)
Рассмотрим влияние реактивных проводимостей на характер нагрузки цепи: 1. 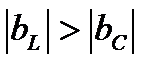 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что  ,
, 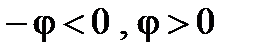 . При этом в данной схеме первая ветвь имеет активно-индуктивный характер нагрузки. Вторая ветвь – активно-ёмкостный характер нагрузки. На рис. 2 приведена векторная диаграмма проводимостей, соответствующая этому случаю. На векторной диаграмме действительные составляющие комплексных проводимостей (активные проводимости схемы
. При этом в данной схеме первая ветвь имеет активно-индуктивный характер нагрузки. Вторая ветвь – активно-ёмкостный характер нагрузки. На рис. 2 приведена векторная диаграмма проводимостей, соответствующая этому случаю. На векторной диаграмме действительные составляющие комплексных проводимостей (активные проводимости схемы  ) представлены векторами, совпадающими или параллельными оси
) представлены векторами, совпадающими или параллельными оси  . Мнимые составляющие комплексных проводимостей (реактивные проводимости схемы
. Мнимые составляющие комплексных проводимостей (реактивные проводимости схемы 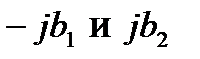 ) представлены векторами параллельными оси
) представлены векторами параллельными оси 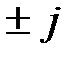 в соответствии с их знаками. Кроме этого указаны как углы
в соответствии с их знаками. Кроме этого указаны как углы 
 , так и углы
, так и углы 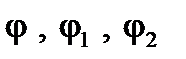 . Учитывая условие 1, в целом, цепь имеет активно-индуктивный характер нагрузки. Прямоугольные треугольники OKN, NBC, OBM носят название треугольников проводимостей.
. Учитывая условие 1, в целом, цепь имеет активно-индуктивный характер нагрузки. Прямоугольные треугольники OKN, NBC, OBM носят название треугольников проводимостей.
Примечание. Направление угла сдвига фаз между напряжением и током принято отсчитывать от тока к напряжению. Поэтому с целью однообразного изложения анализа при построении векторных диаграмм (как и в работе №5) в дальнейшем на них указаны только углы 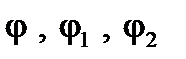 .
.
2. 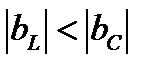 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что 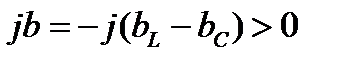 ,
,  . Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится активно-ёмкостным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 3.
. Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится активно-ёмкостным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 3.
|
|
|
3. 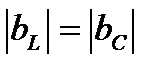 . Из (8) и (11) получим, что
. Из (8) и (11) получим, что 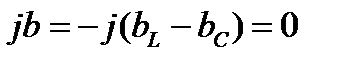 ,
, 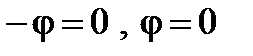 . Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится чисто активным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 4.
. Характер нагрузки каждой ветви не меняется, но характер нагрузки всей схемы становится чисто активным. Векторная диаграмма, соответствующая этому случаю, приведена на рис. 4.
Таким образом, в зависимости от соотношения 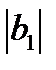 и
и 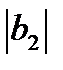 в схеме может происходить частичная или полная компенсация реактивных проводимостей ветвей. Это обстоятельство определяет характер нагрузки реальной цепи, величину и знак фазового угла
в схеме может происходить частичная или полная компенсация реактивных проводимостей ветвей. Это обстоятельство определяет характер нагрузки реальной цепи, величину и знак фазового угла  .
.
Из формул (8) и (10) следует, что
 (12)
(12)
Из (3) будем иметь
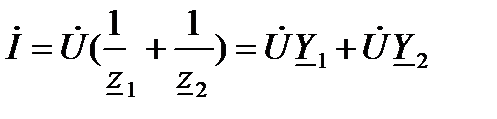 (13)
(13)
Учитывая (9), получим
 (14)
(14)
Слагаемые в правой части (14) имеют размерность А (Ампер). Их принято называть: 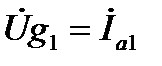 – комплекс активной составляющей действующего значения тока в первой ветви (в целях сокращения эту составляющую тока называют активной составляющей тока в первой ветви. Для остальных составляющих аналогично);
– комплекс активной составляющей действующего значения тока в первой ветви (в целях сокращения эту составляющую тока называют активной составляющей тока в первой ветви. Для остальных составляющих аналогично);  – комплекс активной составляющей тока во второй ветви;
– комплекс активной составляющей тока во второй ветви; 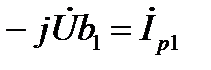 – комплекс реактивной составляющей тока в первой ветви;
– комплекс реактивной составляющей тока в первой ветви;  – комплекс реактивной составляющей тока во второй ветви. Тогда соотношение (14) можно переписать
– комплекс реактивной составляющей тока во второй ветви. Тогда соотношение (14) можно переписать
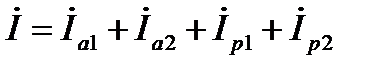 . (15)
. (15)
Соотношению (15) соответствует уже другая эквивалентная схема замещения заданной цепи, состоящая из параллельного соединения активных и реактивных элементов проводимости (рис. 5).
Изобразим на комплексной плоскости соотношение (15). Поскольку 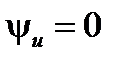 и
и  ,
, 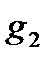 – действительные числа, то вектора
– действительные числа, то вектора 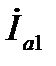 и
и 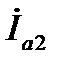 будут совпадать по направлению с вектором
будут совпадать по направлению с вектором 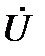 . Т. е. активные составляющие токов в ветвях совпадают по фазе с напряжением на зажимах схемы. вектора
. Т. е. активные составляющие токов в ветвях совпадают по фазе с напряжением на зажимах схемы. вектора  и
и 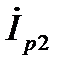 будут перпендикулярны вектору
будут перпендикулярны вектору 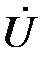 . При этом реактивная составляющая
. При этом реактивная составляющая  отстаёт на угол 90º по фазе, а реактивная составляющая
отстаёт на угол 90º по фазе, а реактивная составляющая 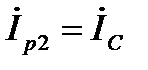 опережает на угол 90º по фазе указанное напряжение. Векторные диаграммы приведены на рис. 6, 7, 8. Они иллюстрируют возможные случаи:
опережает на угол 90º по фазе указанное напряжение. Векторные диаграммы приведены на рис. 6, 7, 8. Они иллюстрируют возможные случаи:
1. Если  , в этом случае
, в этом случае 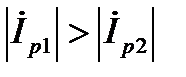 ,
, 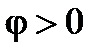 , то общий ток цепи
, то общий ток цепи 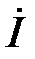 отстаёт по фазе от напряжения
отстаёт по фазе от напряжения 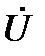 на угол
на угол  (рис. 6);
(рис. 6);
2. Если  , в этом случае
, в этом случае  ,
, 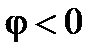 , то общий ток цепи
, то общий ток цепи 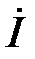 опережает по фазе напряжение
опережает по фазе напряжение 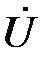 на угол φ (рис. 7);
на угол φ (рис. 7);
3. Наконец, если  , в этом случае
, в этом случае 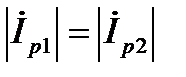 ,
, 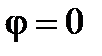 , то общий ток
, то общий ток  цепи совпадает по фазе с напряжением
цепи совпадает по фазе с напряжением  (рис. 8).
(рис. 8).
|
|
|
Следовательно, в цепи происходит частичная или полная компенсация реактивных составляющих токов в ветвях и в зависимости от этого полный (входной) ток 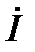 опережает, отстаёт или совпадает по фазе с напряжением
опережает, отстаёт или совпадает по фазе с напряжением  на зажимах цепи.
на зажимах цепи.
Рассмотрим энергетические процессы, протекающие в данной цепи (рис. 1).
Энергетический режим работы каждой ветви, как было установлено в разделе «Основные понятия о цепях синусоидального тока», определяется соотношением её активной и реактивной мощностей. Определим их величину
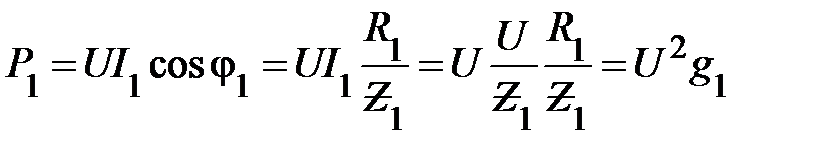 . (16)
. (16)
Аналогично
 (17)
(17)
Т.е. активная или средняя за период мощность каждой ветви в разветвлённой цепи прямо пропорциональна активной проводимости этой ветви. Поскольку Р 1 и Р 2 в каждой ветви характеризуют интенсивность безвозвратного потребления энергии от источника питания, то общая активная мощность цепи равна арифметической сумме активных мощностей каждой ветви и пропорциональна активной проводимости всей цепи
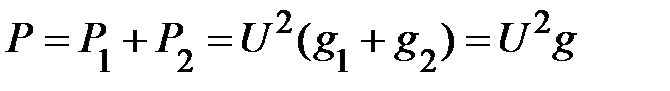 . (18)
. (18)
Определим реактивную мощность
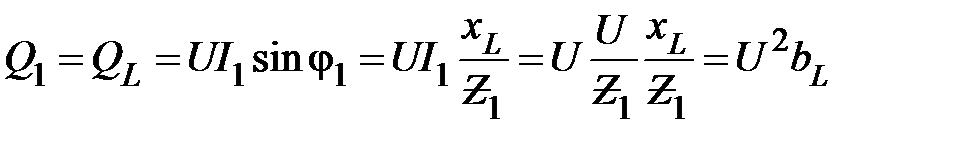 . (19)
. (19)
Аналогично
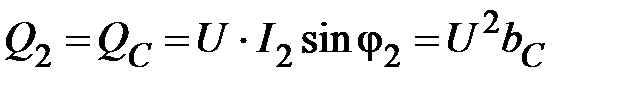 . (20)
. (20)
Т. е. реактивная мощность каждой ветви в разветвлённой цепи прямо пропорциональна реактивной проводимости этой ветви. Для реактивных мощностей можно также записать
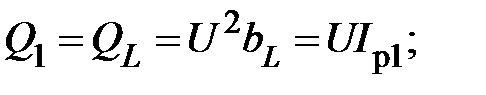 (21)
(21)
 (22)
(22)
При одном и том же напряжении, приложенном к каждой ветви, реактивные составляющие токов этих ветвей 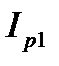 и
и 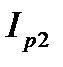 сдвинуты на 180º друг относительно друга. Следовательно, суммарная реактивная мощность равна разности реактивных мощностей в каждой ветви этой цепи
сдвинуты на 180º друг относительно друга. Следовательно, суммарная реактивная мощность равна разности реактивных мощностей в каждой ветви этой цепи
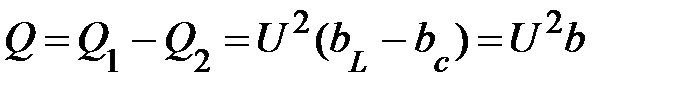 (23)
(23)
и пропорциональна реактивной проводимости всей цепи. Полная мощность каждой ветви равна
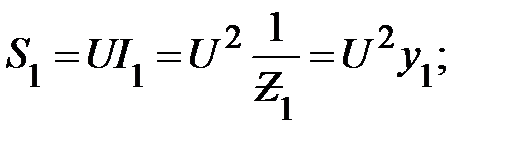 (24)
(24)
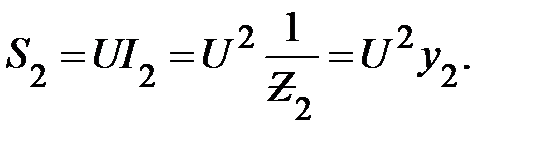 (25)
(25)
Т. е. полная мощность каждой ветви пропорциональна полной проводимости этой ветви. Определим полную мощность всей цепи
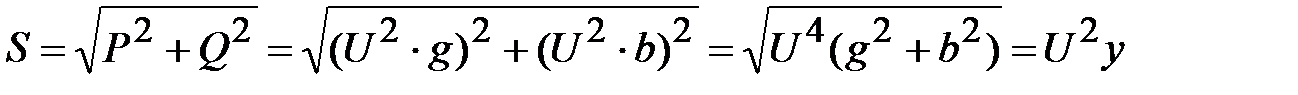 (26)
(26)
Т. е. полная мощность всей цепи пропорциональна проводимости этой цепи.
Для представления полной комплексной мощности с использованием проводимостей введем понятие о комплексно-сопряженных векторах. 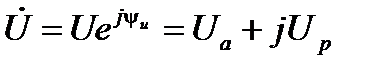 – комплекс действующего значения напряжения,
– комплекс действующего значения напряжения, 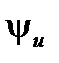 – начальная фаза соответствующей ему синусоиды,
– начальная фаза соответствующей ему синусоиды, 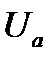 – активная и
– активная и 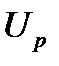 – реактивная составляющие этого комплекса (этого напряжения);
– реактивная составляющие этого комплекса (этого напряжения);  – сопряженный комплекс действующего значения напряжения и его аналогичные составляющие.
– сопряженный комплекс действующего значения напряжения и его аналогичные составляющие.
|
|
|
Такое же представление о сопряженном комплексе можно ввести для тока
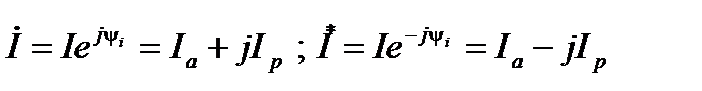 ;
;
для сопряженного комплексного сопротивления
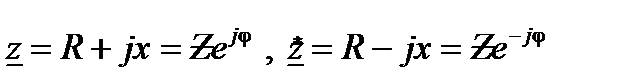 ;
;
для сопряженной комплексной проводимости
 .
.
Рассмотрим известное выражение для полной комплексной мощности
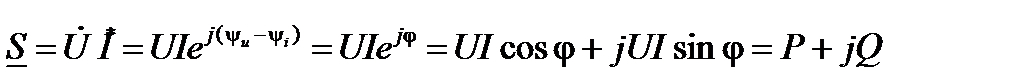 . (27)
. (27)
Таким образом, использование понятия о сопряженном комплексе тока позволяет реализовать аргумент полной комплексной мощности в виде разности фаз между синусоидами напряжения и тока ( ), а также установить корректную математическую связь между полной комплексной мощностью и ее составляющими (
), а также установить корректную математическую связь между полной комплексной мощностью и ее составляющими (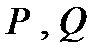 ). Проведем преобразование с сопряженными комплексами. В соответствии с (13) получим
). Проведем преобразование с сопряженными комплексами. В соответствии с (13) получим
 .
.
В таком случае будем иметь
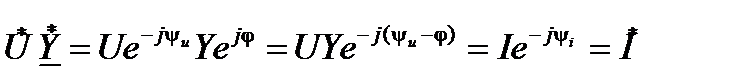 . ( 28)
. ( 28)
Учтем, что
 .
.
То есть для любого параметра произведение комплекса на сопряженный комплекс равно квадрату его модуля.
В соответствии с (27), (28) и (8) рассмотрим полную комплексную мощность
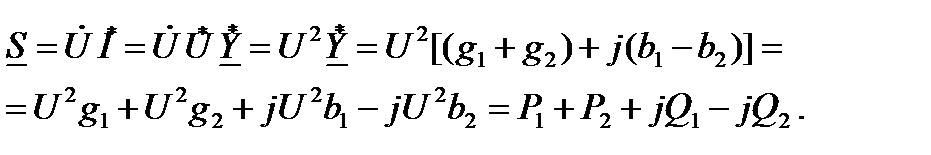 (29)
(29)
Треугольники мощностей, соответствующие выражению (29), приведены на рис. 9, 10, 11, которые иллюстрируют случаи:
– если 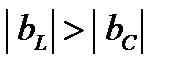 , в этом случае
, в этом случае 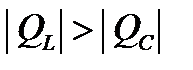 ,
, 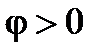 (рис. 9). Т. е. реактивная мощность всей цепи является положительной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между магнитным полем L -элемента и источником питания, а перезаряд С -элемента полностью осуществляется за счёт энергии магнитного поля L - элемента;
(рис. 9). Т. е. реактивная мощность всей цепи является положительной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между магнитным полем L -элемента и источником питания, а перезаряд С -элемента полностью осуществляется за счёт энергии магнитного поля L - элемента;
– если  , в этом случае
, в этом случае  ,
, 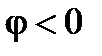 (рис. 10). Т. е. реактивная мощность всей цепи является отрицательной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между электрическим полем С -элемента и источником питания. Энергия в магнитное поле L -элемента полностью поступает при разряде С -элемента;
(рис. 10). Т. е. реактивная мощность всей цепи является отрицательной величиной и во внешней цепи происходит обмен циркулирующей энергией исключительно между электрическим полем С -элемента и источником питания. Энергия в магнитное поле L -элемента полностью поступает при разряде С -элемента;
– наконец, если 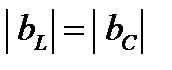 , в этом случае
, в этом случае  , а
, а 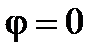 (рис. 11). Т. е. обмена энергией между источником питания и цепью не происходит. Вся энергия, поступающая от источника, безвозвратно потребляется цепью. При этом полная мощность на зажимах цепи чисто активная. Внутри цепи происходит циркулирующий обмен энергией одинаковой интенсивности между полями L, C -элементов.
(рис. 11). Т. е. обмена энергией между источником питания и цепью не происходит. Вся энергия, поступающая от источника, безвозвратно потребляется цепью. При этом полная мощность на зажимах цепи чисто активная. Внутри цепи происходит циркулирующий обмен энергией одинаковой интенсивности между полями L, C -элементов.
Расчёт параметров режима работы цепи, построение векторной диаграммы, треугольников проводимостей и мощностей можно провести, не прибегая к комплексным числам. Расчёт проводят в действующих значениях параметров режима и в модулях параметров цепи. При этом возможны две методики расчёта:
|
|
|
· с использованием понятия об активной и реактивной составляющих тока в каждой ветви;
· с использованием понятия о полной проводимости цепи, ветви и составляющих этих проводимостей.
По первой методике, по известным параметрам цепи определяют полные сопротивления ветвей

Затем определяют полные токи в каждой ветви и составляющие этих токов
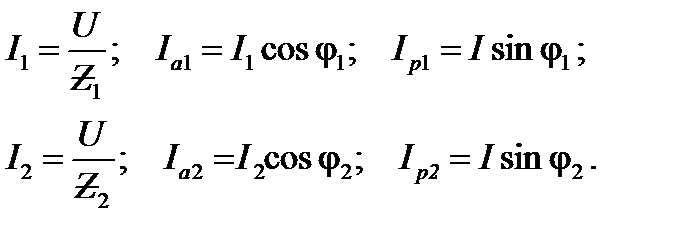
После чего определяют полный (входной) ток цепи
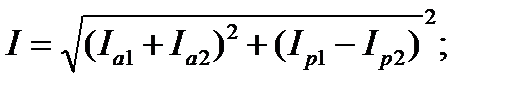
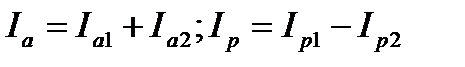
и его фазовый угол
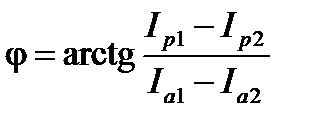 .
.
Рассчитывают мощности на ветвях

мощности на всей схеме
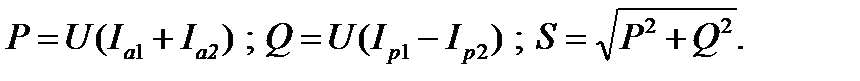
Используя полученные результаты, определяют проводимости ветвей и всей схемы
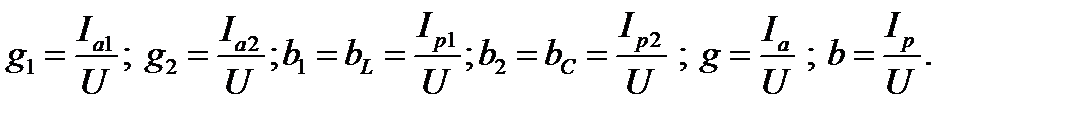
Наконец, по полученным результатам с учётом знаков φ1, φ2 и φ строят векторные диаграммы токов, проводимостей и мощностей.
По второй методике, по известным параметрам цепи определяют проводимости ветвей и их фазовые углы
 .
.
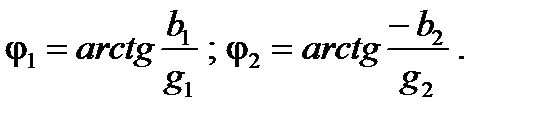
Затем определяют полную проводимость цепи и ее фазовый угол

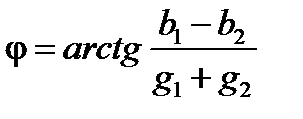 .
.
После чего рассчитывают токи в ветвях и входной ток

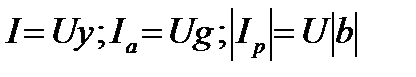 .
.
Определяют мощности ветвей и всей цепи


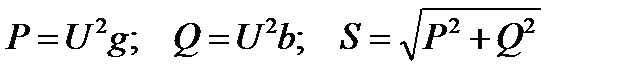 .
.
И, наконец, зная величину  и их знаки, строят векторные диаграммы токов, проводимостей и мощностей.
и их знаки, строят векторные диаграммы токов, проводимостей и мощностей.
Иного характера расчёты проводят, если известны некоторые параметры режима работы цепи, и требуется определить параметры схемы замещения и построить векторную диаграмму. Такие расчёты проводят после экспериментального исследования схемы.
Например, дана схема замещения цепи (рис. 12). Путём эксперимента измерили следующие параметры режима работы этой цепи: P – активную мощность всей цепи; U – напряжение на зажимах цепи; I – входной ток; I 1и I 2 – токи ветвей; угол сдвига фаз  между синусоидами напряжения
между синусоидами напряжения  и тока
и тока 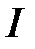 (с учетом его знака). Необходимо определить параметры схемы и построить векторную диаграмму. Проводят следующие расчёты:
(с учетом его знака). Необходимо определить параметры схемы и построить векторную диаграмму. Проводят следующие расчёты:
1. Определяют эквивалентные параметры всей цепи (знак общей реактивной проводимости 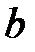 и общего реактивного сопротивления
и общего реактивного сопротивления 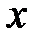 определяется знаком измеренного угла
определяется знаком измеренного угла  )
)
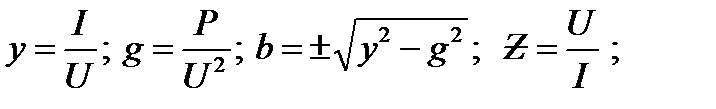
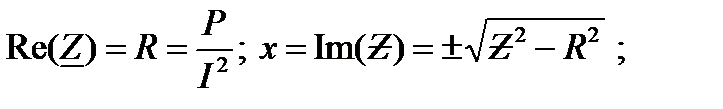 (30)
(30)
2. Определяют эквивалентные параметры каждой ветви
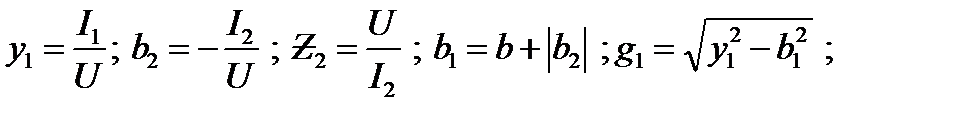
 (31)
(31)
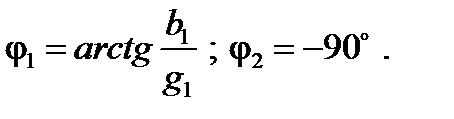
3. Определяют параметры элементов ветвей схемы
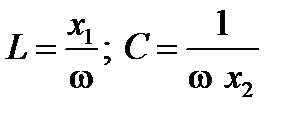 . (32)
. (32)
4. Рассчитывают остальные параметры режима работы схемы
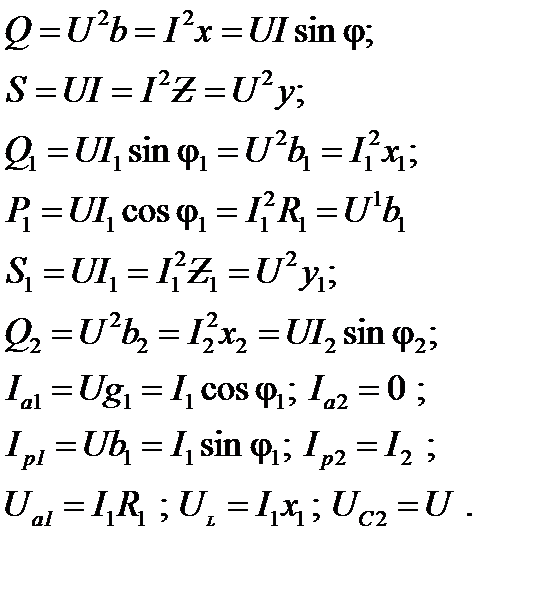 (33)
(33)
5. Строят векторные диаграммы токов, проводимостей, мощностей.
В данной цепи, как и в цепи с последовательным соединением R, L, C - элементов, возможен резонансный режим, который носит название резонанса токов. При резонансе токов в цепи, содержащей L и С- элементы, включённые в параллельные ветви, синусоиды входного тока I и напряжения  , приложенного к зажимам цепи, совпадают по фазе, т. е.
, приложенного к зажимам цепи, совпадают по фазе, т. е.  . Особенности этого режима уже рассмотрены (рис. 4, 8, 11). Определим резонансную частоту в цепи (рис. 1). Если для резонанса токов
. Особенности этого режима уже рассмотрены (рис. 4, 8, 11). Определим резонансную частоту в цепи (рис. 1). Если для резонанса токов 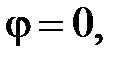 то в соответствии с (11)
то в соответствии с (11)

или
 . (34)
. (34)
Выражение (34) определяет условие резонанса токов для конкретной цепи. Если катушка индуктивности и конденсатор включены в параллельные ветви, то модули реактивных проводимостей ветвей должны быть равны.
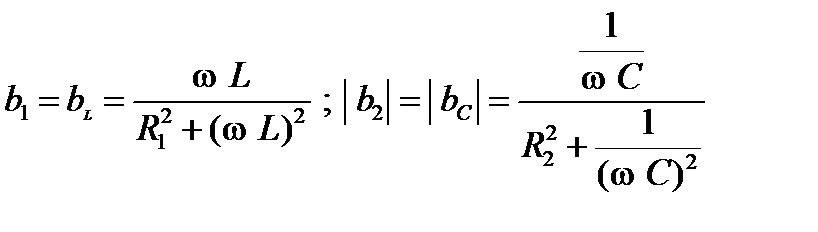 .
.
Подставив эти выражения в (34) и решив уравнение относительно  , получим
, получим
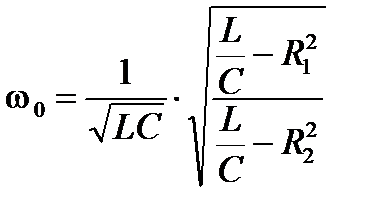 . (35)
. (35)
Выражение (35) показывает, что резонансная частота определяется величиной четырёх параметров цепи L, C, R 1, R 2. Поэтому резонансного режима можно добиться, варьируя каждый из указанных параметров.
Проанализируем зависимости параметров контура и параметров режима его работы от изменения C на примере схемы рис. 12. Считаем, что величина ёмкости С изменяется от 0 до  , а цепь подключена к идеальному источнику синусоидальной ЭДС.
, а цепь подключена к идеальному источнику синусоидальной ЭДС.
Полная проводимость цепи
 .
.
При  Если
Если 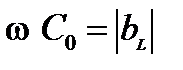 наступает резонансный режим, для которого
наступает резонансный режим, для которого 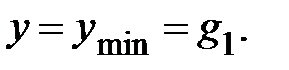 Наконец, если
Наконец, если  Зависимость
Зависимость 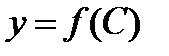 приведена на рис. 13.
приведена на рис. 13.
2. Учитывая, что полное сопротивление цепи  , можно определить характер зависимости
, можно определить характер зависимости 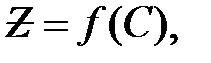 которая также приведена на рис. 13.
которая также приведена на рис. 13.
Коэффициент мощности
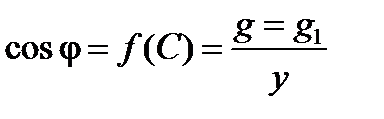 .
.
Эта зависимость будет подобна зависимости  , поскольку g 1 от С не зависит. Зависимость
, поскольку g 1 от С не зависит. Зависимость  поскольку от C этот параметр не зависит и определяется соотношением сопротивлений в первой ветви
поскольку от C этот параметр не зависит и определяется соотношением сопротивлений в первой ветви
 .
.
Для второй ветви 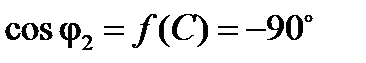 .
.
Токи в цепи
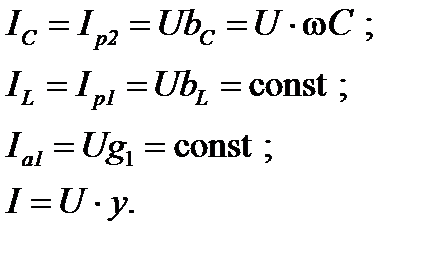
Характер изменения этих зависимостей очевиден и его можно обосновать, используя зависимости, рассмотренные в пунктах 1-3. Графики приведены на рис. 14.
5. Мощности S, P, Q в цепи.
Активная мощность на всей цепи
 ;
;
реактивная мощность изменяется линейно от С
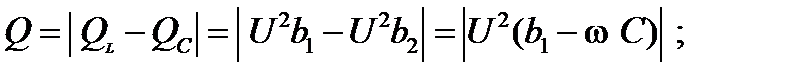
зависимость полной мощности от С подобна зависимости 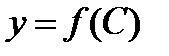 , поскольку
, поскольку
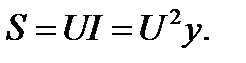
Графики, указанных зависимостей приведены на рис. 15.
Участок цепи, в котором возникает резонанс токов, называют параллельным резонансным контуром. При резонансе токов  в соответствии с (12) становится минимально возможной величиной. Как следует из (5), уменьшая активное сопротивление катушки индуктивности и увеличивая её
в соответствии с (12) становится минимально возможной величиной. Как следует из (5), уменьшая активное сопротивление катушки индуктивности и увеличивая её 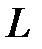 , можно значительно уменьшить и проводимость
, можно значительно уменьшить и проводимость  . Т.е., значительно увеличить сопротивление контура при резонансе токов. Если питать этот контур от источника синусоидального сигнала, ток которого
. Т.е., значительно увеличить сопротивление контура при резонансе токов. Если питать этот контур от источника синусоидального сигнала, ток которого 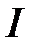 слабо зависит от сопротивления контура (так называемая модель источника тока), то при резонансе токов напряжение на ветвях может в несколько десятков или сотен раз превышать это напряжение при других режимах работы. Это позволяет использовать такие контуры для качественного выделения сигнала определенной (резонансной) частоты во время поиска нужной радиостанции при приеме ее сигнала. Поэтому резонанс токов находит широкое применение в радиотехнике, телевидении, технике проводной электросвязи, измерительной технике, в специальных источниках вторичного электропитания устройств промышленной электроники.
слабо зависит от сопротивления контура (так называемая модель источника тока), то при резонансе токов напряжение на ветвях может в несколько десятков или сотен раз превышать это напряжение при других режимах работы. Это позволяет использовать такие контуры для качественного выделения сигнала определенной (резонансной) частоты во время поиска нужной радиостанции при приеме ее сигнала. Поэтому резонанс токов находит широкое применение в радиотехнике, телевидении, технике проводной электросвязи, измерительной технике, в специальных источниках вторичного электропитания устройств промышленной электроники.
Порядок выполнения работы
1. Собрать экспериментальную электрическую цепь, схема которой приведена на рис. 16.
2. Установить напряжение питания заданной величины по указанию преподавателя.
3. Варьируя величину ёмкости, установить резонансный режим работы экспериментальной цепи. При этом показания фазометра должны быть близки к нулевому значению. Снять показания приборов и занести их таблицу.
4. Уменьшая каждый раз величину ёмкости на 2÷4 мкФ, по сравнению с предыдущим опытом, и поддерживая U =const, проделать 2÷3 опыта. Данные измерений занести в таблицу.
5. Восстановить резонансный режим в цепи. После чего, увеличивая каждый раз величину ёмкости на 2÷3 мкФ по сравнению с предыдущим её значением, проделать 2÷3 опыта, данные занести в таблицу (в каждом опыте напряжение  на входе цепи поддерживается постоянным и равным значению в первом опыте).
на входе цепи поддерживается постоянным и равным значению в первом опыте).
6. Для каждого опыта рассчитать параметры, указанные в таблице 1. Использовать для расчёта соотношения (30) – (33).
Примечание 1. В таблице приведены два столбца, определяющие емкость батареи конденсаторов: C и C ист. В ячейках столбца C указывают величину емкости, набранную на батарее конденсаторов непосредственно перед каждым опытом. В ячейках столбца C ист указывают истинное значение емкости, которое определяют по формуле 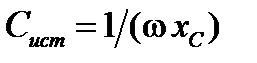 после проведения опытов. При этом
после проведения опытов. При этом  .
.
7. Построить экспериментальные зависимости подобные приведённым на рис. 13, 14, 15.
8. Построить векторные диаграммы токов, треугольники проводимостей и мощностей для трёх опытов (по указанию преподавателя), в которых величина ёмкости выбиралась меньше, равной или больше резонансной.
Примечание 2: При построениях руководствоваться рис. 2, – 4, 6, – 8, 9, – 11, а также учитывать, что для экспериментальной схемы R 2=0. Следовательно, I a2 = 0, g 2 = 0, P 2 = 0.
Рекомендуемая литература
1. Борисов Ю. М., Липатов Д. Н., Зорин Ю.Н. Электротехника. Учебн. Для ВУЗов. М.: Энергоатомиздат, 1985 (подразделы 2.13, 2.14).
2. Электротехника: Учебн. для неэлектротехн. спец. ВУЗов / Под ред. В. Г. Герасимова. М.: Высшая школа, 1985, (подраздел 2.13).
3. Касаткин А. С., Немцов М. В. Электротехника: Учебн. пособие для ВУЗов. М.: Издательский центр «Академия», 2005 (подразделы 2.15, 2.16, 2.17, 2.21).
4. Общая электротехника: Учебн. пособие для ВУЗов / Под ред. Блажкина А. Т. Л.: Энергоатомиздат, 1986 (подразделы 2.8, 2.9, 2.10).
Контрольные вопросы
1. Объяснить построение векторных диаграмм.
2. Объяснить графики экспериментальных зависимостей параметров цепи при изменении С.
3. Какими параметрами определяется сдвиг фаз между входным током и напряжением на зажимах экспериментальной цепи.
4. Условие резонанса токов.
5. Обоснуйте значение каждого параметра режима при резонансе токов по графикам частотных зависимостей.
6. Заданы параметры схемы (рис. 1) L = 0,159 Гн; С = 45,5 мкФ; R 1 = R 2 =40, Ом. Напряжение на зажимах u =150 sin 314 t. Определить (по заданию преподавателя): 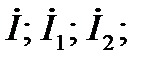
 y 1; g 1; b 1; y 2; g 2; b 2; y; b; g; S; P; Q; S 1; P 1; Q 1; S 2; P 2; Q 2.
y 1; g 1; b 1; y 2; g 2; b 2; y; b; g; S; P; Q; S 1; P 1; Q 1; S 2; P 2; Q 2.
– В схеме (рис. 1) заданы величины параметров 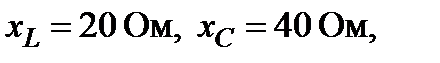
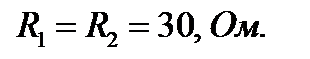 Ом. Амперметр, включённый в первую ветвь, показывает величину 3,А. Определить (по указанию преподавателя):
Ом. Амперметр, включённый в первую ветвь, показывает величину 3,А. Определить (по указанию преподавателя): 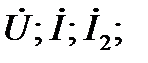

S; P; Q; S 1; P 1; Q 1; S 2; P 2; Q 2.

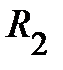

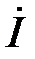
L
C
a
Рис. 1.
+ j
0
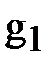
K
M
+1
N
C
B
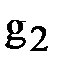
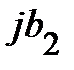

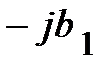

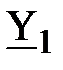


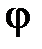


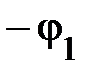
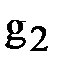


Рис. 2.
0
+ j
+1
N
C
K
M
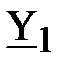

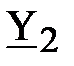
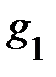

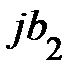


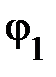
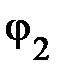
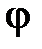
B
Рис. 3.
0
K
M(B)
+1
C
N
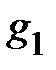
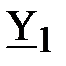
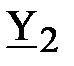
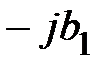


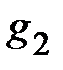
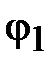
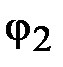
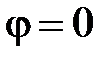
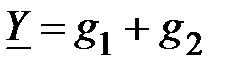
+ j
Рис. 4.
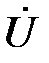
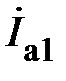
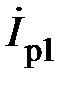
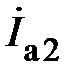
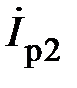
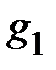
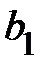

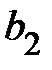
Рис. 5.
+ j
0
+1


