 |
Г. В. Красоленко, Н. В. Сванидзе, Г. В. Якунина
|
|
|
|
Министерство образования и науки Российской Федерации
Санкт-Петербургский государственный
архитектурно-строительный университет
Факультет городского строительства и жилищно-коммунального хозяйства
Кафедра математики
Г. В. КРАСОЛЕНКО, Н. В. СВАНИДЗЕ, Г. В. ЯКУНИНА
Обыкновенные дифференциальные уравнения. Ряды
Рабочая программа, методические указания и
контрольные задания
Санкт-Петербург
УДК 519. 95 (075. 8)
Рецензент канд. физ. -мат. наук, доцент Е. К. Ершов (СПбГАСУ)
Обыкновенные дифференциальные уравнения. Ряды: рабочая программа, методические указания и контрольные задания / сост.: Г. В. Красоленко, Н. В. Сванидзе, Г. В. Якунина; СПбГАСУ. – СПб., 2012. – 53 с
Даются методические рекомендации по выполнению индивидуального домашнего задания (пятой и шестой контрольных работ) по курсу высшей математики: «Обыкновенные дифференциальные уравнения. Ряды » и предназначены для студентов факультета безотрывной формы обучения.
Приводятся варианты контрольных работ.
Библиогр.: 7 назв.
Ó Санкт-Петербургский государственный
архитектурно-строительный университет, 2012
ВВЕДЕНИЕ
Прежде чем приступать к выполнению контрольных работ, Вам необходимо ознакомиться с «Рабочей программой» и изучить соответствующий теоретический материал по учебникам, указанным в разделе «Рекомендуемая литература».
Во время экзаменационной сессии для студентов безотрывной формы обучения читают установочные лекции и проводят практические занятия, которые носят обзорный характер.
К сдаче экзамена или зачета допускаются студенты, контрольные работы которых проверены и зачтены преподавателями кафедры математики.
|
|
|
Обратите внимание на оформление контрольной работы. На титульном листе должны быть указаны:
фамилия, имя, отчество
Номер студенческого билета (или зачетной книжки)
Специальность
Название дисциплины и номер контрольной работы
Номер варианта
Номер варианта, который должен выполнять студент, соответствует последней цифре номера студенческого билета (или зачетной книжки). Цифре ноль соответствует вариант № 10
РАБОЧАЯ ПРОГРАММА КУРСА ВЫСШЕЙ МАТЕМАТИКИ
Обыкновенные дифференциальные уравнения
1. Определение обыкновенного дифференциального уравнения. Порядок уравнения. Определение решения уравнения.
2. Общий вид дифференциального уравнения первого порядка. Решение уравнения. Геометрическая трактовка перечисленных понятий для уравнения 1-го порядка. Теорема существования и единственности решения дифференциального уравнения первого порядка. Решения уравнения (общее, частное и особое). Задача Коши для уравнения 1-го порядка. Основные типы дифференциальных уравнений первого порядка, допускающие решение в квадратурах (уравнения с разделяющимися переменными, линейные и Бернулли).
3. Общий вид дифференциального уравнения порядка 
. Общий интеграл и общее решение дифференциального уравнения порядка . Теорема существования и единственности решения дифференциального уравнения – го порядка. Задача Коши для уравнения – го порядка.
4. Основные классы дифференциальных уравнений высшего порядка, приводимых к уравнению первого порядка: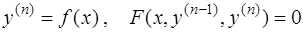 
и 
5. Общий вид линейного однородного и неоднородного уравнений порядка . Свойства частных решений линейного однородного уравнения второго порядка (суперпозиции решений, вронскиан решений). Формула Лиувилля для вронскиана
|
|
|
6. Линейная зависимость и линейная независимость частных решений линейного однородного уравнения второго порядка. Необходимое и достаточное условия линейной независимости частных решений. Структура общего решения линейного однородного и неоднородного уравнений.
7. Определение комплексных чисел. Алгебраическая форма комплексного числа. Действия над комплексными числами в алгебраической форме. Модуль и аргумент комплексного числа. Тригонометрическая форма комплексных чисел. Действия над комплексными числами в тригонометрической форме. Формула Муавра. Формулы Эйлера. Показательная форма комплексного числа.
8. Нахождение линейно независимых частных решений линейного однородного уравнения 2-го порядка с постоянными коэффициентами.
9. Метод вариации произвольных постоянных (метод Лагранжа).
10. Нахождение частных решений линейного неоднородного уравнения 2-го порядка с постоянными коэффициентами со специальной правой частью 
методом неопределенных коэффициентов.
11. Понятие о нормальной системе дифференциальных уравнений, ее общем решении и задаче Коши. Сведение дифференциального уравнения – го порядка к нормальной системе дифференциальных уравнений. Линейные однородные и неоднородные системы дифференциальных уравнений и свойства их решений.
|
|
|
