 |
Примерный вариант контрольной работы № 5
|
|
|
|
Ряды
1. Понятие о ряде, его общем члене, частичной сумме и сумме (в случае его сходимости). Частичный остаток ряда. Эквивалентность ряда и его частичного остатка в отношении сходимости. Геометрическая прогрессия.
2. Необходимый признак сходимости и его недостаточность. Арифметические операции со сходящимися рядами.
3. Знакопостоянные ряды. Общий признак сходимости рядов с положительными членами. Два признака сходимости рядов с положительными членами, основанные на сравнении рядов (в предельной и непредельной формах).
4. Признак Даламбера в предельной и непредельной формах. Оценка частичного остатка ряда, удовлетворяющего условиям признака сходимости Даламбера.
5. Интегральный признак Коши. Оценка частичного остатка ряда, удовлетворяющего условиям интегрального признака сходимости.
6. Знакочередующиеся ряды. Признак сходимости Лейбница. Оценка частичного остатка ряда, удовлетворяющего условиям признака сходимости Лейбница.
7. Теорема о сходимости ряда при условии сходимости ряда из абсолютных величин его членов. Абсолютно и неабсолютно (условно) сходящиеся ряды. Свойства абсолютно сходящихся рядов. Теорема Римана.
8. Степенной ряд комплексной переменной. Теорема Абеля. Область и радиус сходимости степенного ряда комплексной переменной.
9. Вещественный степенной ряд, его промежуток и радиус сходимости. Свойства степенного ряда вещественной переменной (непрерывность суммы ряда, дифференцирование и интегрирование степенного ряда).
10. Разложение функции в степенной ряд. Единственность разложения. Ряд Тейлора функции.
11. Формула Тейлора функции. Представление остаточного члена формулы Тейлора в интегральной форме и в форме Лагранжа. Необходимые и достаточные условия разложимости функции в ряд Тейлора.
|
|
|
12. Разложение в степенные ряды по степеням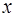 
функций 
, 
, 
, 
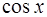и 
13. Разложение в степенные ряды по степеням 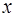функци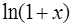й 
, 
и 
.
14. Тригонометрический ряд и его физическая трактовка. Ортогональность системы тригонометрических функций. Выражение коэффициентов тригонометрического ряда через его сумму. Ряд Фурье функции.
15. Теорема Дирихле. Разложение в ряд Фурье четных и нечетных функций. Разложение в ряд Фурье функций на половине промежутка периодичности.
Примерный вариант контрольной работы № 5
по теме «Обыкновенные дифференциальные уравнения»
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
3) 
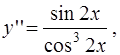
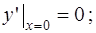
4) 
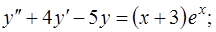
5) 
Решение задачи № 1
Важным теоретическим вопросом в теории дифференциальных уравнений является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и поэтому приходиться ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решений данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности (см. [2] и [4]).
Во всех вариантах контрольной работы дифференциальное уравнение первого порядка можно представить в виде, разрешенном относительно первой производной:
(1)
где функция 
определена в некоторой области 
на плоскости 
Множество точек на плоскости называется областью, если оно открыто и связно. Открытость означает, что вместе с каждой своей точкой множество содержит и некоторый круг с центром в этой точке. Связность означает, что любые две точки можно соединить ломаной, целиком содержащейся в . В частности, плоскость 
является областью.
|
|
|
Для уравнения (1) справедлива следующая теорема.
|
|
|
