 |
Уравнение (7) называется характеристическим уравнением дифференциального уравнения (3).
|
|
|
|
Уравнение (7) называется характеристическим уравнением дифференциального уравнения (3).
Напомним формулу для определения двух корней 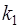 и
и 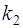 квадратного уравнения (7). Пусть дискриминант
квадратного уравнения (7). Пусть дискриминант  , тогда
, тогда
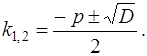 (8)
(8)
При решении квадратного уравнения (7) возможны три случая в зависимости от знака дискриминанта  :
:
1) корни уравнения 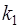 и
и 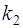 вещественные и различные
вещественные и различные 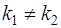
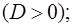
2) корни уравнения 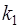 и
и 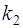 вещественные и равные
вещественные и равные 
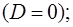
3) корни уравнения 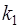 и
и 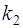 – комплексно сопряженные числа
– комплексно сопряженные числа 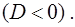
Рассмотрим каждый из этих случаев.
1. Корни уравнения 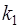 и
и 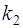 вещественные и различные
вещественные и различные 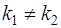 . Тогда уравнение(3) имеет два решения
. Тогда уравнение(3) имеет два решения 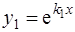 и
и 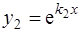 . Они линейно независимы, так как
. Они линейно независимы, так как
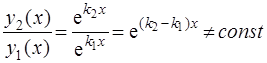
и, следовательно, общее решение уравнения (3) имеет вид
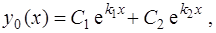 (9)
(9)
где 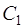 и
и 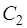 – произвольные постоянные.
– произвольные постоянные.
2. Пусть корни характеристического уравнения 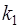 и
и 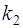 вещественные и равные
вещественные и равные  . Тогда линейное однородное уравнение (3) имеет два линейно независимых решения
. Тогда линейное однородное уравнение (3) имеет два линейно независимых решения  и
и  (см. [2] и [4]) и, следовательно, общее решение уравнения (3) имеет вид
(см. [2] и [4]) и, следовательно, общее решение уравнения (3) имеет вид
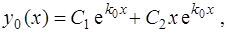 (10)
(10)
где 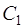 и
и 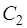 – произвольные постоянные.
– произвольные постоянные.
3. Пусть корни характеристического уравнения 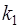 и
и 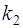 – комплексно сопряженные числа
– комплексно сопряженные числа  , где
, где 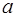 и
и 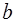 – вещественные числа, причем
– вещественные числа, причем 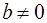 ,
, 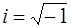 – мнимая единица (см. [2] и [4]). Тогда линейное однородное уравнение (3) имеет два линейно независимых решения
– мнимая единица (см. [2] и [4]). Тогда линейное однородное уравнение (3) имеет два линейно независимых решения 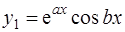 и
и 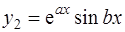 и, следовательно, общее решение уравнения (3) имеет вид
и, следовательно, общее решение уравнения (3) имеет вид
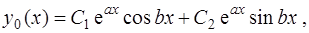 (11)
(11)
где 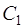 и
и 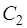 – произвольные постоянные.
– произвольные постоянные.
II. Построение частного решения линейного неоднородного уравнения со специальной правой частью. Метод неопределенных коэффициентов
Этот метод применим тогда, когда в правой части уравнения (1) стоит функция специального вида (2). В этом случае частное решение 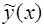 уравнения может быть найдено в соответствии с видом его правой части.
уравнения может быть найдено в соответствии с видом его правой части.
|
|
|
Рассмотрим здесь два частных варианта специальных правых частей.
1. Пусть в формуле (2) число 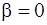 , тогда уравнение (1) имеет вид
, тогда уравнение (1) имеет вид
 (12)
(12)
где 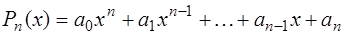 – многочлен степени
– многочлен степени 
 , а вещественное число
, а вещественное число  является контрольным числом.
является контрольным числом.
Уравнению (12) соответствует однородное уравнение
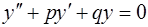
с характеристическим уравнением
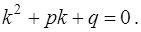 (13)
(13)
Пусть 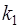 и
и 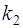 его корни.
его корни.
Имеет место следующее утверждение (см. [2]).
Утверждение 3.
Частное решение уравнения (12) следует искать в виде:
a) если контрольное число  не является корнем характеристического уравнения (13), т. е.
не является корнем характеристического уравнения (13), т. е. 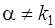 и
и 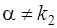 , то
, то
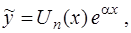
где 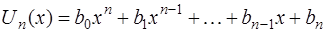 – многочлен той же степени
– многочлен той же степени  , что и многочлен
, что и многочлен  , с коэффициентами
, с коэффициентами  , подлежащими дальнейшему определению;
, подлежащими дальнейшему определению;
b) если контрольное число  является простым корнем характеристического уравнения (13), т. е.
является простым корнем характеристического уравнения (13), т. е. 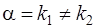 или
или 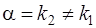 , то
, то
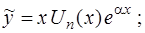
c) если контрольное число  является кратным корнем характеристического уравнения (13), т. е.
является кратным корнем характеристического уравнения (13), т. е. 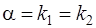 , то
, то

Приведем сводную таблицу.

где 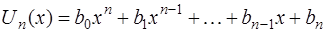 – многочлен той же степени
– многочлен той же степени  , что и многочлен
, что и многочлен  , с коэффициентами
, с коэффициентами  , подлежащими дальнейшему определению.
, подлежащими дальнейшему определению.
Коэффициенты 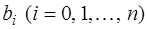 многочлена
многочлена 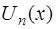 должны быть такими, чтобы функция
должны быть такими, чтобы функция 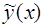 удовлетворяла уравнению (12). Поэтому для их отыскания используют следующий алгоритм.
удовлетворяла уравнению (12). Поэтому для их отыскания используют следующий алгоритм.
С помощью утверждения 3 устанавливается вид частного решения 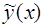 .
.
Затем определяются производные 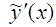 и
и 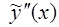 . Решение
. Решение 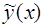 и его производные с неопределенными пока коэффициентами подставляются в уравнение (12) и обе его части сокращаются на
и его производные с неопределенными пока коэффициентами подставляются в уравнение (12) и обе его части сокращаются на  .
.
Далее, мы определяем коэффициенты 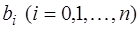 , исходя из тождественного равенства двух многочленов, стоящих в левой и правой частях уравнения (12)
, исходя из тождественного равенства двух многочленов, стоящих в левой и правой частях уравнения (12)
(два многочлена равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях переменной 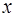 ).
).
|
|
|
Решение задачи № 4
Найдем общее решение уравнения
 (14)
(14)
Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами. Его общее решение ищем в виде  . Неоднородному уравнению (14) соответствует однородное уравнение
. Неоднородному уравнению (14) соответствует однородное уравнение
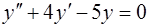 . (15)
. (15)
Функция 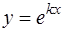 является решением уравнения (15), если
является решением уравнения (15), если 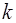 есть корень характеристического уравнения
есть корень характеристического уравнения
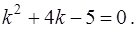 (16)
(16)
Оно имеет корни  (вещественные и различные). Следовательно, общее решение однородного уравнения (15) имеет вид
(вещественные и различные). Следовательно, общее решение однородного уравнения (15) имеет вид
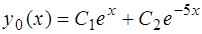 .
.
Построим теперь частное решение 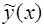 уравнения (14). В нашем случае правая часть уравнения (14)
уравнения (14). В нашем случае правая часть уравнения (14)
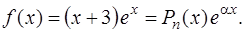
Сравнивая два последних выражения, получаем 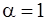 и
и 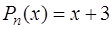 – многочлен первой степени,
– многочлен первой степени,  .
.
Поскольку контрольное число  совпадает с корнем характеристического уравнения
совпадает с корнем характеристического уравнения  (
(  – простой корень характеристического уравнения (16)), частное решение уравнения (14) следует искать в виде
– простой корень характеристического уравнения (16)), частное решение уравнения (14) следует искать в виде
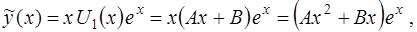
где коэффициенты  и
и  подлежат определению.
подлежат определению.
Чтобы найти  и
и  , подставим
, подставим 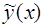 и его производные в исходное уравнение (14). Здесь при вычислении
и его производные в исходное уравнение (14). Здесь при вычислении  удобно воспользоваться формулой
удобно воспользоваться формулой 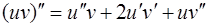 .
.
Итак,
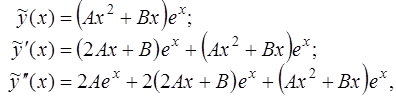
и левая часть уравнения (14) принимает вид
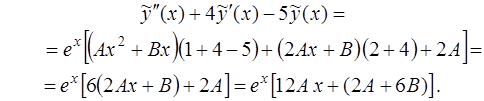
В результате для определения коэффициентов  и
и  получаем уравнение
получаем уравнение
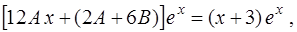
обе части которого можно сократить на множитель  .
.
Коэффициенты  и
и  должны быть такими, чтобы обе части уравнения (14) были тождественно равны друг другу, т. е.
должны быть такими, чтобы обе части уравнения (14) были тождественно равны друг другу, т. е.
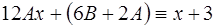 . (17)
. (17)
Тождество (17) выполняется тогда и только тогда, когда слева и справа стоят одинаковые коэффициенты при одинаковых степенях 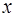 :
:

Следовательно,  ,
, 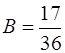 , а
, а 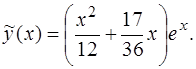
Таким образом, общее решение уравнения (14) имеет вид

Ответ. Общим решением уравнения (14) является функция

определенная на интервале 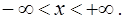
2. Рассмотрим решение линейного неоднородного уравнения (1) со специальной правой частью
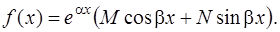
Предполагается, что контрольные числа 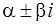 мнимые, т. е.
мнимые, т. е.  , а
, а 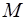 и
и 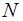 – вещественные числа, заданные многочлены нулевой степени (см. формулу (2)).
– вещественные числа, заданные многочлены нулевой степени (см. формулу (2)).
Уравнение (1) в этом случае принимает вид
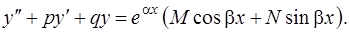 (18)
(18)
Уравнению (18) соответствует однородное уравнение
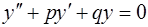
с характеристическим уравнением
 . (19)
. (19)
|
|
|
Пусть 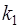 и
и 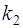 его корни.
его корни.
Имеет место следующее утверждение (см. [2]).
|
|
|


