 |
Решение задачи № 2. является знакочередующимся рядом, т.е. рядом следующего вида
|
|
|
|
Решение задачи № 2
Данный ряд
(1)
является знакочередующимся рядом, т. е. рядом следующего вида
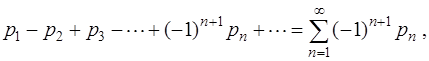
где все члены последовательности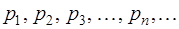 
положительны.
Исследуем ряд (1) на абсолютную сходимость. Для этого составим ряд из абсолютных величин членов исходного ряда
(2)
Получили ряд с положительными членами 
где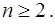 
Для исследования сходимости ряда (2) применим интегральный признак Коши.
Теорема. Пусть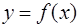 
– непрерывная неотрицательная убывающая функция, определенная при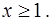 
Если несобственный интеграл
сходится, то сходится и ряд 
Если интеграл расходится, то ряд расходится.
В нашем случае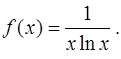 
При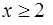 
эта функция удовлетворяет всем условиям интегрального признака: она принимает положительные значения, непрерывная, убывающая и 
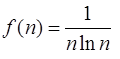при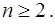
Рассмотрим несобственный интеграл
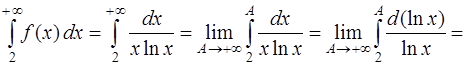
Интеграл расходится, значит и ряд (2) расходится. Следовательно, исходный ряд (1) не имеет абсолютной сходимости.
Исследуем теперь ряд (1) на условную сходимость, используя признак Лейбница.
Теорема. Пусть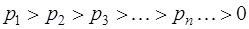 
и 
тогда ряд
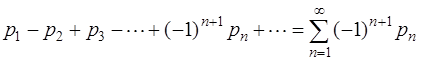
сходится.
Очевидно, что условия теоремы для ряда (1) выполняются:
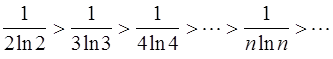и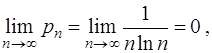 
следовательно, ряд сходится. Так как ряд (2), составленный из абсолютных величин членов исходного ряда, расходится, то знакочередующийся ряд (1) сходится условно или неабсолютно.
Ответ. Ряд сходится условно.
Решение задачи № 3
В этой задаче рассматривается степенной ряд, т. е. бесконечный ряд вида
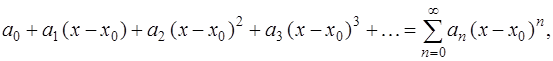(1)
где 
фиксированные числа, а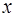 
пробегает некоторый интервал. Точнее, ряд (1) называется степенным рядом с центром или рядом по степеням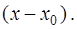 
Центр сходимости степенного ряда задачи 3 находится в точке 
так как 
|
|
|
Исследование сходимости степенного ряда основано на использовании следующей теоремы, которая является следствием теоремы Абеля.
Теорема. Пусть дан степенной ряд 
тогда существует такое число 
(которое может также принимать значение 
), что ряд абсолютно сходится при 
и расходится при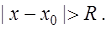 
При 
и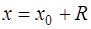 
ряд может либо сходиться, либо расходиться.
Число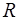 
называется радиусом сходимости рассматриваемого ряда, а интервал 
его интервалом сходимости (в предположении, конечно, что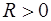 
). Интервал сходимости можно представить в виде 
Если закрепить конкретное значение 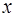, то степенной ряд (1) превращается в бесконечный числовой ряд, который может либо сходиться, либо расходиться.
Для определения интервала сходимости степенного ряда воспользуемся признаком Даламбера, применив его к ряду из абсолютных величин членов исходного ряда
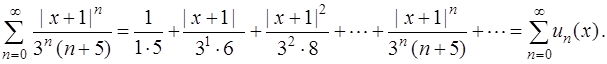(2)
Так как 
то 
и
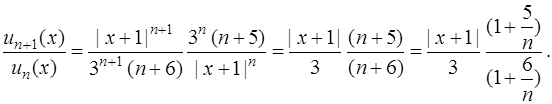
Напоминаем, что мы закрепили конкретное значение .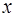
Найдем предел
В соответствии с признаком Даламбера (см. решение задачи 1) ряд (2) сходится, а исходный ряд сходится абсолютно, если значения переменной 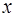удовлетворяют неравенству
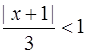или 
Отсюда видно, что радиус сходимости степенного ряда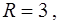 
центр 
мы определили ранее.
Интервал сходимости степенного ряда представим в следующем виде
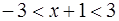или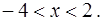 
Остается определить поведение степенного ряда на концах интервала сходимости 
и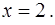 
При получаем знакочередующийся числовой ряд
(3)
При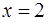 
получаем числовой ряд с положительными членами
(4)
Начинать исследование на сходимость нужно с ряда (4), так как он составлен из абсолютных величин членов ряда (3). Если ряд (4) сходится, то решение на этом практически заканчивается.
|
|
|
Заметим, что не следует повторно применять признак Даламбера при исследовании на сходимость ряда (4), так как концевые точки и 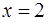интервала сходимости являются решением уравнения
В этом случае признак Даламбера не работает.
Применим к исследованию ряда (4) интегральный признак Коши (см. решение задачи 2).
Тогда 
непрерывная положительная убывающая функция, определенная при 
Поскольку интеграл
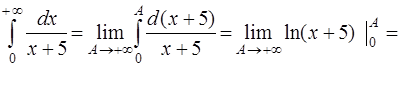
расходится, то расходится и ряд (4).
Следовательно, ряд (3) не имеет абсолютной сходимости. Исследуем его на условную сходимость с помощью признака Лейбница.
Так как
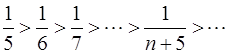и 
то условия признака Лейбница выполнены, и значит, знакочередующийся ряд (3) сходится условно (или неабсолютно).
Ответ. Степенной ряд сходится абсолютно на интервале 
, при ряд сходится условно (или неабсолютно), на интервалах 
и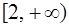 
ряд расходится.
|
|
|
