 |
Решение задачи № 4. который называется рядом Тейлора в точке. . Контрольная работа № 5. по теме « Обыкновенные дифференциальные уравнения»
|
|
|
|
Решение задачи № 4
В этой задаче требуется разложить данную функцию в степенной ряд и указать интервал, на котором это разложение справедливо.
Напомним, что если функция 
в некоторой окрестности точки 
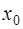имеет производные любого порядка, то для нее можно построить степенной ряд
(1)
который называется рядом Тейлора в точке .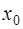
В формуле (1) использованы следующие обозначения:
· производная нулевого порядка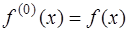 
совпадает с самой функцией;
· функция 
факториал определяется следующим образом:
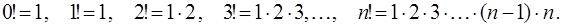
Частичные суммы ряда Тейлора называют многочленами Тейлора функции в точке .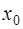
При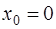 
ряд Тейлора называют рядом Маклорена.
Функция , определенная в некоторой окрестности точки 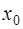, называется аналитической в точке 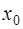, если ее можно представить в виде суммы сходящегося степенного ряда с центром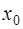
В этом случае говорят, что функция разлагается в ряд Тейлора по степеням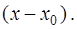 
Функция , определенная вблизи 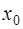и имеющая производные всех порядков, не обязана быть аналитической в этой точке. Может случиться, что ее ряд Тейлора имеет нулевой радиус сходимости или ненулевой радиус сходимости, но сумма его не равна .
При разложении в ряд многих элементарных функций можно использовать известные разложения функций в ряд Маклорена:
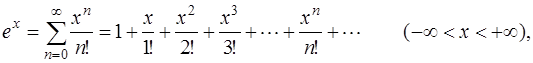
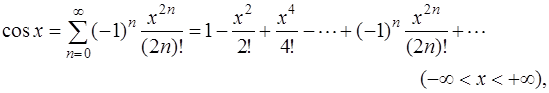
Для того, чтобы разложить функцию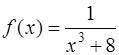 
в ряд по степеням 
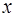мы воспользуемся биномиальным разложением (результат принадлежит Ньютону)
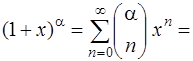
Здесь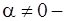 
любое действительное число и биномиальные коэффициенты определяются следующими формулами
Так как наша функция может быть представлена в виде
|
|
|
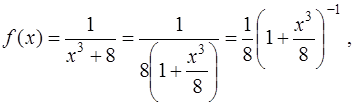
то мы воспользуемся биномиальным разложением с показателем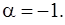 
Вычислим биномиальные коэффициенты при этом значении 
В результате получим разложение
Заменяя здесь 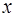на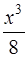 
, получим требуемое разложение функции
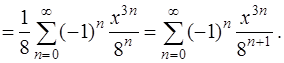
Это разложение справедливо, когда
или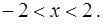 
Ответ. 
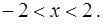
Решение задачи № 5
Эту задачу можно решать разными способами. Мы рассмотрим только один из них. По условию задачи предполагается, что решение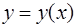 
дифференциального уравнения можно разложить в степенной ряд с центром в 
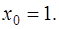В силу теоремы единственности разложения функции в степенной ряд, этот ряд есть ряд Тейлора.
Так как требуется написать разложение 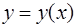в ряд до членов порядка 
включительно, то это означает, что в качестве приближенного решения задачи Коши берем многочлен Тейлора четвертой степени функции 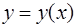в точке 
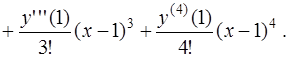
Напомним, что частичные суммы ряда Тейлора называют многочленами Тейлора функции 
в точке .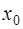
Первые два коэффициента определяются из начальных условий
Коэффициент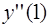 
находим из уравнения 
. Подставляя в него начальные условия, получаем
Для вычисления производных 
и 
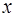продифференцируем уравнение по переменной два раза, используя правило дифференцирования сложной функции,
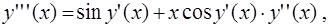
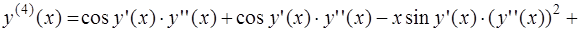
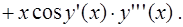
Вычислим их значения при 
Учитывая, что
получаем 
Подставим найденные значения производных в многочлен Тейлора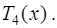 
В результате получим
Ответ.
Контрольная работа № 5
по теме « Обыкновенные дифференциальные уравнения»
Вариант № 1
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
3) 
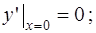
4) 
5) 
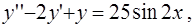
Вариант № 2
Определить тип дифференциального уравнения и найти его решение:
|
|
|
1) 
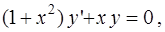
2) 
3) 
4) 
5) 
Вариант № 3
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
3) 
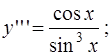
4) 
5) 
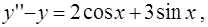
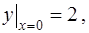
Вариант № 4
Определить тип дифференциального уравнения и найти его решение:
1) 
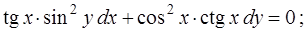
2) 
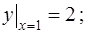
3) 
4) 
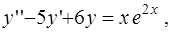
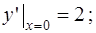
5) 
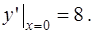
Вариант № 5
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
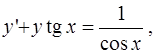
3) 
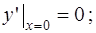
4) 
5) 
Вариант № 6
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
3) 
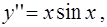
4) 
5) 
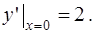
Вариант № 7
Определить тип дифференциального уравнения и найти его решение:
1) 
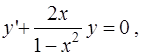
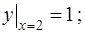
2) 
3) 
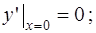
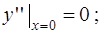
4) 
5) 
Вариант № 8
Определить тип дифференциального уравнения и найти его решение:
1) 
2) 
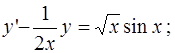
3)
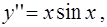
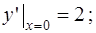
4) 
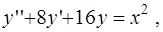
5) 
Вариант № 9
Определить тип дифференциального уравнения и найти его решение:
1) 
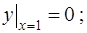
2) 
3) 
4) 
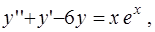
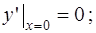
5) 
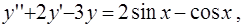
Вариант № 10
Определить тип дифференциального уравнения и найти его решение:
1) 
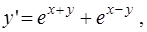
2) 
3) 
4) 
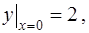
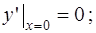
5) 
|
|
|
