 |
Утверждение 4. Решение задачи № 5. Примерный вариант контрольной работы № 6. по теме « Ряды». где и – неизвестные числа, подлежащие дальнейшему определению;
|
|
|
|
Утверждение 4.
Частное решение уравнения (18) следует искать в виде:
a) если контрольные числа 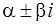 не являются корнями характеристического уравнения (19), т. е.
не являются корнями характеристического уравнения (19), т. е.  , то
, то
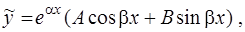
где  и
и  – неизвестные числа, подлежащие дальнейшему определению;
– неизвестные числа, подлежащие дальнейшему определению;
b) если контрольные числа 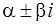 являются корнями характеристического уравнения (19), т. е.
являются корнями характеристического уравнения (19), т. е.  , то
, то
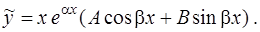
Заметим, что искомое частное решение всегда содержит оба слагаемых  вне зависимости от того, содержит ли функция, стоящая в правой части уравнения (18), одновременно
вне зависимости от того, содержит ли функция, стоящая в правой части уравнения (18), одновременно  и
и 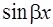 .
.
Числа  и
и  определяются непосредственной подстановкой решения
определяются непосредственной подстановкой решения 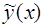 и его производных в уравнение (18).
и его производных в уравнение (18).
Для того чтобы уравнение превратилось в тождество, приравняем коэффициенты при 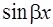 и
и  в его левой и правой частях.
в его левой и правой частях.
В результате получим систему линейных уравнений для нахождения  и
и  .
.
Решение задачи № 5
Решить задачу Коши:
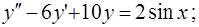 (20)
(20)
 (21)
(21)
Это линейное неоднородное уравнение второго порядка с постоянными коэффициентами.
Его общее решение ищем в виде 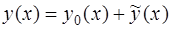 .
.
Неоднородному уравнению (20) соответствует однородное уравнение
 (22)
(22)
Функция 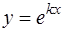 является решением уравнения (22) в том случае, если
является решением уравнения (22) в том случае, если 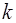 есть корень характеристического уравнения
есть корень характеристического уравнения
 (23)
(23)
Оно имеет два комплексно сопряженных корня
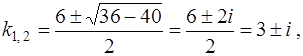
т. е. 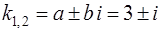 , где
, где  и
и  .
.
Следовательно, общее решение однородного уравнения (22) в соответствии с формулой (11) имеет вид

Построим теперь частное решение 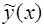 уравнения (20).
уравнения (20).
Для уравнения (20)
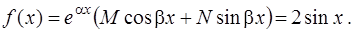
Отсюда имеем 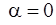 ,
,  ,
,  и
и  .
.
Частное решение 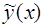 следует искать в виде
следует искать в виде

поскольку контрольные числа 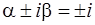 не совпадают с корнями
не совпадают с корнями 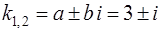 характеристического уравнения (23).
характеристического уравнения (23).
|
|
|
Коэффициенты  и
и  подлежат определению.
подлежат определению.
Вычислим первую и вторую производные функции 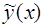


После подстановки 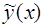 ,
,  и
и  в левую часть (20) имеем:
в левую часть (20) имеем:

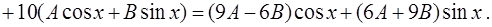
Следовательно,  и
и  должны обеспечивать выполнение тождества
должны обеспечивать выполнение тождества
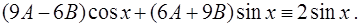
Отсюда, приравнивая коэффициенты при 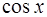 и
и  в его левой и правой частях, получим систему линейных уравнений с двумя неизвестными
в его левой и правой частях, получим систему линейных уравнений с двумя неизвестными  и
и  :
:

Решая эту систему, находим

Общее решение уравнения (20) имеет вид
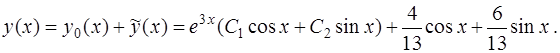 (24)
(24)
Найдем теперь значения постоянных 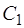 и
и  , при которых выполняются начальные условия (21). Согласно первому из них
, при которых выполняются начальные условия (21). Согласно первому из них
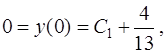
откуда  .
.
Продифференцируем общее решение (24)

Согласно второму из равенств (21) имеем
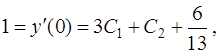
откуда найдем  .
.
Подставив найденные значения 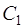 и
и 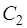 в общее решение (24), получаем искомое частное решение
в общее решение (24), получаем искомое частное решение
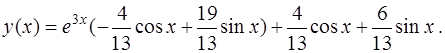
Ответ.
Решением задачи Коши (20), (21) является функция 
определенная на интервале 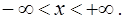
Примерный вариант контрольной работы № 6
по теме « Ряды»
1) Найти общий член, записать ряд с помощью сигма – символики и исследовать его на сходимость:

2) Исследовать на абсолютную и условную сходимость знакочередующийся ряд:

3) Определить интервал сходимости степенного ряда и исследовать его поведение на концах этого интервала:

4) Разложить функцию 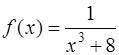 в ряд Маклорена, используя разложение основных элементарных функций. Указать интервал сходимости;
в ряд Маклорена, используя разложение основных элементарных функций. Указать интервал сходимости;
5) Найти решение дифференциального уравнения в виде степенного ряда:
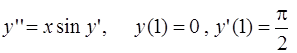 (до членов порядка
(до членов порядка  включительно).
включительно).
Решение задачи № 1
Перед нами ряд с положительными членами. Найдем формулу его общего члена  ,
,  Заметим, что числа
Заметим, что числа  , стоящие в числителях членов нашего ряда, образуют арифметическую прогрессию с первым членом
, стоящие в числителях членов нашего ряда, образуют арифметическую прогрессию с первым членом 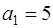 и разностью
и разностью 
Напомним, что числовая последовательность 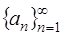 , каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом
, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом 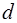 , называется арифметической прогрессией. Число
, называется арифметической прогрессией. Число 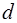 – разность прогрессии.
– разность прогрессии.
|
|
|
Общий член арифметической прогрессии определяется по формуле 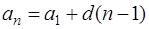 , где
, где 
В нашем случае 
Числа 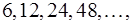 стоящие в знаменателях членов нашего ряда, образуют геометрическую прогрессию с первым членом
стоящие в знаменателях членов нашего ряда, образуют геометрическую прогрессию с первым членом  и знаменателем
и знаменателем 
Числовая последовательность 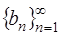 , каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число
, каждый член которой, начиная со второго, равен предыдущему, умноженному на одно и то же число  , называется геометрической прогрессией. Число
, называется геометрической прогрессией. Число  – знаменатель прогрессии.
– знаменатель прогрессии.
Общий член геометрической прогрессии определяется по формуле  где
где  Считаем, что
Считаем, что 
В нашей задаче 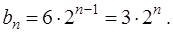
Таким образом, общий член ряда можно записать в виде
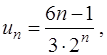 где
где 
Сигма – символика. Мы будем пользоваться сокращенным обозначением для сумм, содержащим букву 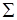 (греческая прописная буква «сигма»). Пусть задано правило, сопоставляющее каждому целому числу
(греческая прописная буква «сигма»). Пусть задано правило, сопоставляющее каждому целому числу  , взятому из некоторого набора целых чисел
, взятому из некоторого набора целых чисел  число
число  . Условимся, что
. Условимся, что
 обозначает сумму
обозначает сумму 
Переменная  здесь «немая».
здесь «немая».
Сигма – символика используется и для бесконечных числовых рядов 
В нашей задаче
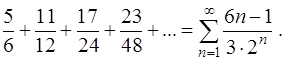
Приступим к исследованию данного ряда на сходимость. Воспользуемся сначала необходимым признаком сходимости ряда.
Теорема. Если ряд  сходится, то
сходится, то 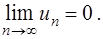
Найдем

Здесь при раскрытии неопределенности  применено правило Лопиталя.
применено правило Лопиталя.
Необходимый признак выполнен, но о сходимости ряда ничего сказать нельзя.
Применим теперь к данному ряду достаточный признак – признак частных Даламбера.
Теорема. Пусть все члены ряда  положительны.
положительны.
Если  то ряд сходится.
то ряд сходится.
Если же  то ряд расходится.
то ряд расходится.
Так как общий член ряда 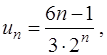 то для нахождения
то для нахождения 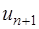 заменим
заменим  на
на 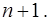 В результате получим
В результате получим
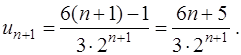
Составим отношение  члена ряда к
члена ряда к 

и найдем предел

Следовательно, на основании признака Даламбера рассматриваемый ряд сходится.
Замечание. Иногда проверить выполнение необходимого признака сходимости трудно, поэтому следует сразу попытаться применить один из достаточных признаков сходимости ряда.
Ответ. Ряд 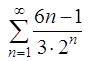 сходится.
сходится.
|
|
|


