8.4 СПИРАЛЬ. Рис. 144. Спираль. Схема сил. Характеристики спирали. Уравнения движения на спирали, их анализ. Рис. 144. Спираль. Схема сил. Характеристики спирали.

8. 4 СПИРАЛЬ

Спираль – фигура пилотажа (пространственная), при выполнении которой вертолет движется по спиральной траектории с набором высоты или снижением.

Спираль с креном до 30° называется мелкой, а с креном более 30° – глубокой. Согласно КУЛП и КБП спираль на вертолете Ми-8 выполняется с креном не более 15°.

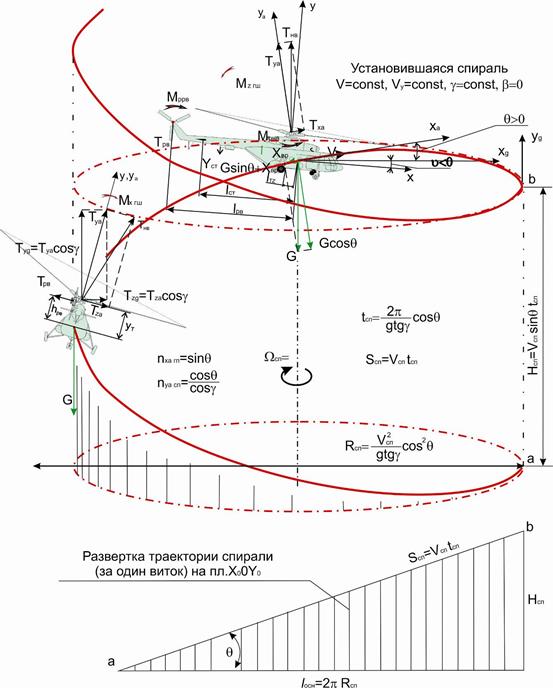
Рис. 144. Спираль. Схема сил. Характеристики спирали.

Спираль с набором высоты – восходящая (рис. 144), а с потерей высоты – нисходящая.

Назначение данной фигуры – выполнить быстрый набор высоты или снижение в ограниченном пространстве с целью ведения наблюдения или ухода на маршрут (посадки).

Нисходящая спираль возможна с работающими двигателямии на режиме самовращения НВ.

При выполнении спирали вертолет находится в сложном движении, т. е. он кроме вращения относительно пространственной оси 00₁ и оси 0y увеличивает или уменьшает высоту полета.

Основные кинематические характеристики траектории спирали:

- R_сп  – радиус спирали;

- Ω _сп – угловая скорость спирали;

- Н_сп – шаг спирали, т. е. набор высоты за один виток (за один разворот на 360º ).

Установившейся считается спираль, если в процессе выполнения кинематические характеристики траектории не изменяются. Ее траектория – винтовая линия. Неустановившаяся спираль – если хотя бы один из параметров спирали изменяется во времени.

Установившаяся правильная спираль выполняется с постоянными значениями угла крена, поступательной и вертикальной скоростями, без скольжения.

При развертке траектории такой спирали (за I виток) на вертикальную плотность угол ее наклона траектории остается постоянным. Фактически спираль сочетает выполнение виража с одновременным набором высоты или снижением по наклонной траектории. Поэтому схема сил и моментов на виде сзади аналогична схеме сил и моментов на вираже, а на виде сбоку аналогична схеме сил и моментов в наборе (снижении) по наклонной траектории.

 

Уравнения движения на спирали, их анализ

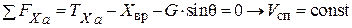;                          (8. 29)

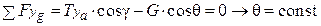;                                   (8. 30)

 .      (8. 31)

Так как силы Т_Zа∙ сosγ и Т_РВ∙ сosγ равны, то сила Ту_а∙ sinγ является центростремительной силой, искривляющей траекторию движения (неуравновешенная сила).

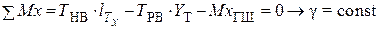;                    (8. 32)

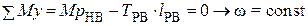;                                (8. 33)

 .   (8. 34)

Вывод. По сравнению с правильным виражом при выполнении установившейся восходящей спирали с теми же значениями угла крена и скорости полета требуется большая мощность СУ, так как вертолет не только разворачивается, но и набирает высоту. Выполнение нисходящей спирали при прочих равных условиях требует, наоборот, меньшей мощности СУ по сравнению с правильным виражом. И очевидно, что при одинаковой располагаемой мощности вертикальная скорость на восходящей спирали меньше, чем при наборе высоты по наклонной траектории.

Характеристики спирали

 

Характеристики спирали определяются из уравнений 8. 29 – 8. 31, но вначале надо выразить их через перегрузки, т. е.

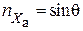;                                                    (8. 35)

;                                                   (8. 36)

 .                                       (8. 37)

1. Перегрузка тангенциальная (n_Xа) и нормальная (n_ya) определяются по формулам 8. 35 и 8. 36.

ВыводЫ:

- тангенциальная перегрузка во всем диапазоне допустимых углов наклона траектории на спирали меньше I, 0 (так при θ = 25⁰ → n_Xсп = 0, 25, при θ = 30⁰ → n_Xсп = 0, 5);

- так как на нисходящей спирали 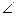θ < 0, то и продольная перегрузка n_Xсп < 0;

- нормальная перегрузка на спирали меньше, чем на вираже при том же угле крена (так при γ = 15° и θ = 12° → n_Усп = 0, 97, в то время как на вираже при том же крене n_Усп = 1, 04);

- при θ = 0 → сosθ = 1, т. е. вертолет выполняет вираж.

2. Радиус спирали определяется из уравнения (8. 37)

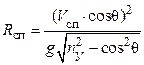или ;                     (8. 38)

R_сп  = R_В ∙ сosθ.

Вывод. При прочих равных условиях разворот вертолета в спирали осуществляется с меньшим радиусом, чем в вираже из-за искривления траектории маневра не только в горизонтальной, но и в вертикальной плоскости.

3. Время разворота на 360° (I виток) определяется:

;

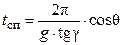 или  .                        (8. 39)

Вывод. При прочих равных условиях время выполнения одного витка спирали меньше, чем время выполнения виража, хотя вертолет проходит больший путь. Это связано с дополнительным исправлением траектории в вертикальной плоскости.

4. Шаг спирали, т. е. высота, которую набирает (теряет) вертолет за один виток. Он определяется из развертки витка спирали, проложенного по образующей цилиндра радиуса «R_СП»:

H_сп = 2π ∙ R_сп ∙ tgθ;

Н_сп = V ∙ sinθ ∙ t_сп = V_у ∙ t_сп.                                 (8. 40)

Выводы:

- все формулы служат для расчета характеристик восходящей и нисходящей установившихся спиралей;

⇐ Предыдущая23242526272829303132Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: