 |
2.3 Оценка результатов обучения при проведении промежуточной аттестации по учебному предмету 2 страница
|
|
|
|
| Контрольная точка №1 | ||
| Тема | «Корни, степени, логарифмы» | |
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. | |
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |
| 1 вариант А1. Вычислите а) б) А2. Решите уравнение: а) б) А3. Решите неравенство А4. Найдите область определения функции В1. Решите уравнение В2. Решите уравнение В3. Найдите область определения функции С1. Вычислите:
| 2 вариант
А1. Вычислите
а)  .
б) .
б) 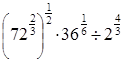 .
А2. Решите уравнение: а) .
А2. Решите уравнение: а) 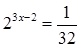 ;
б) ;
б)  .
А3. Решите неравенство .
А3. Решите неравенство  .
А4. Найдите область определения функции .
А4. Найдите область определения функции 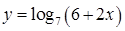 .
В1. Решите уравнение .
В1. Решите уравнение  .
В2. Решите уравнение .
В2. Решите уравнение  .
В3. Найдите область определения функции .
В3. Найдите область определения функции  .
С1. Вычислите: .
С1. Вычислите: 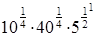 . .
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки |
|
Раздел Прямые и плоскости в пространстве | |||
| Тема 7. Взаимное расположение прямых в пространстве. | ЛРN2, 3 МРN4, 5 ПРN1, 6 | Формулировка и приведение доказательств признаков взаимного расположения прямых и плоскостей. Распознавание на чертежах и моделях различных случаев взаимного расположения прямых и плоскостей, аргументирование своих суждений. | Сообщение Письменная проверочная работа |
| Тема 8. Плоскости в пространстве | ЛРN2 МРN4, 5 ПРN6 | Формулирование определений, признаков и свойств параллельных и перпендикулярных плоскостей, двугранных и линейных углов. Выполнение построения углов между прямыми, прямой и плоскостью, между плоскостями по описанию и распознавание их на моделях. Применение признаков и свойств расположения прямых и плоскостей при решении задач. | Устный опрос Письменная проверочная работа |
| Тема 9. Перпендикулярность прямых и плоскостей. | ЛРN2 МРN4, 5 ПРN6 | Изображение на рисунках и конструирование на моделях перпендикуляров и наклонных к плоскости, прямых, параллельных плоскостей, углов между прямой и плоскостью и обоснование построения. Решение задач на вычисление геометрических величин. Описывание расстояния от точки до плоскости, от прямой до плоскости, между плоскостями, между скрещивающимися прямыми, между произвольными фигурами в пространстве. | Устный опрос Контрольная точка №2 |
| Тема 10. Геометрические преобразования пространства | ЛРN2, 3 МРN5, 6 ПРN6, 8 | Формулирование и доказывание основных теорем о расстояниях (теорем существования, свойства). Изображение на чертежах и моделях расстояния и обоснование своих суждений. Определение и вычисление расстояний в пространстве. Применение формул и теорем планиметрии для решения задач. Ознакомление с понятием параллельного проектирования и его свойствами. | Практическое занятие |
Сообщения
|
|
|
| Темы сообщений | Критерий оценивания |
| Основные понятия и аксиомы стереометрии. Геометрия Евклида, как первая научная система. Геометрия формы в искусстве. Взаимосвязь архитектуры и математики. Взаимное расположение прямых и плоскостей в пространстве. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Устный опрос
|
|
|
| Вопросы для устного контроля по разделу | Критерии оценивания |
| Что относится к основным понятиям стереометрии (точка, прямая, плоскость, пространство). Раскрыть понятие аксиоматического способа построения геометрии. Дать определение: пересекающиеся, параллельные и скрещивающиеся прямые, угол между прямыми в пространстве. Перпендикулярность прямых. Параллельность и перпендикулярность прямой и плоскости, признаки и свойства. Теорема о трех перпендикулярах. Перпендикуляр и наклонная к плоскости. Угол между прямой и плоскостью. Параллельность плоскостей, перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Расстояния от точки до плоскости. | Оценка «5» ставится, если обучающийся полно излагает материал (отвечает на вопрос), дает правильное определение основных понятий; обнаруживает понимание материала, может обосновать свои суждения, применить знания на практике . Оценка «4» ставится, если обучающийся дает ответ, удовлетворяющий тем же требованиям, что и для оценки «отлично», но допускает 1–2 ошибки, которые сам же исправляет. Оценка «3» ставится, если обучающийся обнаруживает знание и понимание основных положений данной темы, но излагает материал неполно и допускает неточности в определении понятий или формулировке правил. Оценка «2» ставится, если обучающийся обнаруживает незнание большей части соответствующего вопроса, допускает ошибки в формулировке определений и правил, искажающие их смысл, беспорядочно и неуверенно излагает материал |
|
|
|
Письменная проверочная работа
| Письменная проверочная работа №5
| ||||
| Тема | Взаимное расположение прямых в пространстве | |||
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы | |||
| 1 вариант А1. Точка М не принадлежит плоскости треугольника АВС. Каково взаимное расположение прямых МА и ВС? Ответ обоснуйте.
А2. На рисунке 1 прямая НА пересекает плоскость АВС. Каково взаимное расположение прямых ОН и РК? Ответ обоснуйте.
| 2 вариант
А1. Точка М не принадлежит плоскости четырехугольника АВСD. Каково взаимное расположение прямых МD и ВС? Ответ обоснуйте.
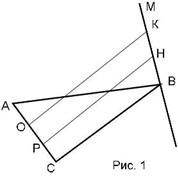 А2. На рисунке 1 прямая МВ пересекает плоскость АВС. Каково взаимное расположение прямых ОК и РН? Ответ обоснуйте.
А2. На рисунке 1 прямая МВ пересекает плоскость АВС. Каково взаимное расположение прямых ОК и РН? Ответ обоснуйте.
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Письменная проверочная работа
| Письменная проверочная работа №6
| ||
| Тема | Параллельность плоскостей. Тетраэдр и параллелепипед | |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы | |
| 1 вариант А1. Сторона АС треугольника АВС лежит в плоскости
А2. В тетраэдре DABC постройте сечение плоскостью, проходящей через середину ребра DC, вершину В и параллельной прямой АС.
А3. В параллелепипеде ABCDA1B1C1D1 точки К, Р и М принадлежат соответственно ребрам АА1, А1В1 и ВС. Постройте сечение параллелепипеда плоскостью КРМ.
| 2 вариант
А1. Сторона АВ треугольника АВС лежит в плоскости  . Через середину АС – точку Р проведена плоскость . Через середину АС – точку Р проведена плоскость  , параллельная плоскости , параллельная плоскости  и пересекающая ВС в точке Е. Найдите АВ, если РЕ = 7 см.
А2. В тетраэдре DABC постройте сечение плоскостью, проходящей через вершину А, точку М ребра DВ, параллельной прямой ВС.
А3. В параллелепипеде ABCDA1B1C1D1 точки Р, Н и К принадлежат соответственно ребрам В1С1, СС1 и АВ. Постройте сечение параллелепипеда плоскостью РНК. и пересекающая ВС в точке Е. Найдите АВ, если РЕ = 7 см.
А2. В тетраэдре DABC постройте сечение плоскостью, проходящей через вершину А, точку М ребра DВ, параллельной прямой ВС.
А3. В параллелепипеде ABCDA1B1C1D1 точки Р, Н и К принадлежат соответственно ребрам В1С1, СС1 и АВ. Постройте сечение параллелепипеда плоскостью РНК.
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Практическое занятие
| Практическое занятие №3 | |||||
| Тема | Изучение основ параллельного проектирования и его свойств. Перпендикуляр и наклонные | ||||
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | ||||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| ||||
| 1 вариант Задание: С помощью тени изобразить возможные варианты параллельных проекций плоских фигур на плоскость и сделать вывод. Для этого используем разные модели
Вариант 1 Треугольник, четырехугольник, окружность. Решить задачи: А1. В треугольнике АВС АС = ВС = 10 см,
А2. Отрезок АМ является перпендикуляром к плоскости прямоугольника АВСD. Угол между прямой МС и этой плоскостью равен 300,
В1. Даны две параллельные плоскости и множество треугольников таких, что в каждом треугольнике две вершины принадлежат первой из двух данных плоскостей, а третья вершина – второй. Какую фигуру образует множество всех точек пересечения медиан треугольников?
| 2 вариант
Задание: С помощью тени изобразить возможные варианты параллельных проекций плоских фигур на плоскость и сделать вывод. Для этого используем разные модели
Вариант 2
Прямоугольник, овал, равносторонний треугольник.
Решить задачи:
А1. В треугольнике АВС угол С прямой, а  . Через точку С проведена прямая СМ, перпендикулярная плоскости треугольника, АС = 18см,
СМ = 12 см. Найдите расстояние от точки М до прямой АВ и расстояние от точки В до плоскости ACМ.
А2. Отрезок ВМ является перпендикуляром к плоскости параллелограмма АВСD. Угол между прямой МА и этой плоскостью равен 600. . Через точку С проведена прямая СМ, перпендикулярная плоскости треугольника, АС = 18см,
СМ = 12 см. Найдите расстояние от точки М до прямой АВ и расстояние от точки В до плоскости ACМ.
А2. Отрезок ВМ является перпендикуляром к плоскости параллелограмма АВСD. Угол между прямой МА и этой плоскостью равен 600.  , АВ = 20 см. Найдите расстояние от точки М до плоскости АВС. __________________________________
В1. Даны две параллельные плоскости , АВ = 20 см. Найдите расстояние от точки М до плоскости АВС. __________________________________
В1. Даны две параллельные плоскости  и и  и множество треугольников таких, что одна сторона каждого треугольника лежит в плоскости и множество треугольников таких, что одна сторона каждого треугольника лежит в плоскости  , а середина другой – в плоскости , а середина другой – в плоскости  . Какую фигуру образует множество вершин этих треугольников, не принадлежащих плоскости . Какую фигуру образует множество вершин этих треугольников, не принадлежащих плоскости  ? ?
| ||||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. | ||||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | ||||
Контрольная точка
| Контрольная точка №2 | |
| Тема | Расположение прямых и плоскостей в пространстве |
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. |
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы |
| 1 вариант Параллельность прямых и плоскостей А1. Основание AD трапеции АВСD лежит в плоскости а) Каково взаимное расположение прямых ЕF и АВ? б) Чему равен угол между прямыми ЕF и АВ, если А2. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС в точке В1. Найдите длину отрезка А1В1, если АВ = 15 см, АА1: АС = 2: 3. В1. Даны параллелограмм АВСD и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках А1, В1, С1, D1. Найдите длину отрезка DD1, если АА1 = 2 м, BB1 = 3 м, СС1 = 8 м. Перпендикулярность прямых и плоскостей А1. Диагональ куба равна 6 см. Найдите: а) ребро куба; б) косинус угла между диагональю куба и плоскостью одной из его граней. А2. Из точки к плоскости проведены две наклонные, равные 23 см и 33 см. Найдите расстояние от этой точки до плоскости, если проекции наклонных относятся как 2: 3 _______________________________________________ В1. В ромбе АВСD угол А равен 60о, сторона ромба равна 4 см. Прямая АЕ перпендикулярна плоскости ромба. Расстояние от точки Е до прямой DC равно 4 см. Найдите расстояние от точки Е до плоскости ромба и от точки А до плоскости ЕDC.
2 вариант Параллельность прямых и плоскостей А1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны АD, точка К – середина стороны DC. а) Каково взаимное расположение прямых РК и АВ? б) Чему равен угол между прямыми РК и АВ, если А2. Дан треугольник АВС. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке А1, а сторону ВС в точке В1. Найдите длину отрезка А1В1, если В1С = 10 см, АВ: ВС = 4: 5. В1. Даны параллелограмм АВСВ и не пересекающая его плоскость. Через вершины параллелограмма проведены параллельные прямые, пересекающие данную плоскость в точках А1, В1, С1, D1. Найдите длину отрезка DD1, если АА1 = 4 м, BB1 = 3 м, СС1 = 1 м. Перпендикулярность прямых и плоскостей А1. Основанием прямоугольного параллелепипеда служит квадрат, диагональ параллелепипеда равна а) измерения параллелепипеда; б) синус угла между диагональю параллелепипеда и плоскостью его основания.
А2. Из точки к плоскости проведены две наклонные, равные 10 см и 17 см. Разность проекций этих наклонных равна 9 см. Найдите проекции этих наклонных. В1. Через основание трапеции проведена плоскость, отстоящая от другого основания на расстояние а. Найдите расстояние от точки пересечения диагоналей трапеции до этой плоскости, если основания трапеции относятся как m: n.
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % |
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки |
|
Раздел Комбинаторика | |||
| Тема 11. Основные понятия комбинаторики | ЛРN1, 7 МРN6, 7 ПРN7 | Изучение правила комбинаторики и применение при решении комбинаторных задач. Решение комбинаторных задач методом перебора и по правилу умножения. Ознакомление с понятиями комбинаторики: размещениями, сочетаниями, перестановками и формулами для их вычисления. Объяснение и применение формул для вычисления размещений, перестановок и сочетаний при решении задач. Ознакомление с биномом Ньютона и треугольником Паскаля. Решение практических задач с использованием понятий и правил комбинаторики | Сообщение Практическое занятие |
Сообщения
| Темы сообщений | Критерий оценивания |
| История развития комбинаторики. Комбинаторика вокруг нас. Комбинаторика и ее роль в различных сферах человеческой деятельности. Треугольник Паскаля. Бином Ньютона. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Практическое занятие
| Практическое занятие №4 | ||
| Тема | Изучение истории развития комбинаторики, теории вероятностей и статистики и их роль в различных сферах человеческой жизнедеятельности, правил комбинаторики. Решение комбинаторных задач | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| 1 вариант 1. Из цифр 0, 2, 3, 4 составьте все возможные двузначные числа при условии, что: а) цифры в числе не повторяются; б) допускается повторение цифр в числе. 2. В коридоре висят четыре лампочки. Сколько имеется различных способов освещения коридора? 3. Вычислите: 4. Вычислите: 5. Найдите коэффициент при первой степени переменной х у многочлена Р(х) = (1+2х)8. | 2 вариант
1. Из цифр 1, 2, 3, 4 составьте все возможные трехзначные числа при условии, что:
а) цифры в числе не повторяются;
б) допускается повторение цифр в числе.
2. При встрече 6 человек обменялись рукопожатиями. Сколько всего было сделано рукопожатий?
3. Вычислите: 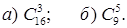 4. Вычислите:
4. Вычислите:  5. Найдите коэффициент при второй степени переменной х у многочлена
Р(х) = (3 - х)7.
5. Найдите коэффициент при второй степени переменной х у многочлена
Р(х) = (3 - х)7.
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки |
|
Раздел Координаты и векторы | |||
| Тема 12. Прямоугольная (декартова) система координат в пространстве | ЛРN2, 3 МРN1, 4 ПРN6, 8 | Изучение декартовой системы координат в пространстве, построение по заданным координатам точек и плоскостей, нахождение координат точек. Нахождение уравнений окружности, сферы, плоскости. Вычисление расстояний между точками. | Сообщение Письменная проверочная работа |
| Тема 13. Векторы. Действия с векторами. | ЛРN6 МРN2, 3 ПРN6 | Ознакомление с понятием вектора. Изучение свойств векторных величин, правил разложения векторов в трехмерном пространстве, правил нахождения координат вектора в пространстве, правил действий с векторами, заданными координатами. Применение теории при решении задач на действия с векторами. Изучение скалярного произведения векторов, векторного уравнения прямой и плоскости. Применение теории при решении задач на действия с векторами, координатный метод, применение векторов для вычисления величин углов и расстояний. Ознакомление с доказательствами теорем стереометрии о взаимном расположении прямых и плоскостей с использованием векторов | Устный опрос Практическое занятие Контрольная точка № 3 |
|
|
|



 .
.  .
. 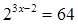 ;
;  .
. 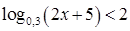 .
. 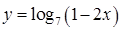 .
.  .
. 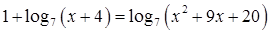 .
.  .
.  .
. 
 . Прямая BD перпендикулярна плоскости треугольника, BD = 5см. Найдите расстояние от точки D до прямой АС и расстояние от точки В до плоскости ADC.
. Прямая BD перпендикулярна плоскости треугольника, BD = 5см. Найдите расстояние от точки D до прямой АС и расстояние от точки В до плоскости ADC. 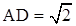 , CD = 2. Найдите АМ. ______________________________________
, CD = 2. Найдите АМ. ______________________________________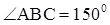 ? Ответ обоснуйте.
? Ответ обоснуйте.  ? Ответ обоснуйте.
? Ответ обоснуйте.  см, а его измерения относятся как 1: 1: 2. Найдите:
см, а его измерения относятся как 1: 1: 2. Найдите: