 |
2.3 Оценка результатов обучения при проведении промежуточной аттестации по учебному предмету 3 страница
|
|
|
|
Сообщения
| Темы сообщений | Критерий оценивания |
| История декартовой системы координат. Векторы в пространстве. Координаты и векторы. Действия с векторами. Использование векторов в науках и практической жизни. Геометрия Евклида, как первая научная система. Геометрия Лобачевского как пример аксиоматической теории. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Устный опрос
|
|
|
| Вопросы для устного контроля по разделу | Критерии оценивания |
| 1. Декартовы координаты в пространстве. 2. Формула расстояния между двумя точками. 3. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости. 4. Векторы. Модуль вектора. Равенство векторов. Сложение векторов и умножение вектора на число. Угол между векторами. 5. Координаты вектора. Скалярное произведение векторов. 6. Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам. 7. Компланарные векторы. Разложение по трем некомпланарным векторам. | Оценка «5» ставится, если обучающийся полно излагает материал (отвечает на вопрос), дает правильное определение основных понятий; обнаруживает понимание материала, может обосновать свои суждения, применить знания на практике . Оценка «4» ставится, если обучающийся дает ответ, удовлетворяющий тем же требованиям, что и для оценки «отлично», но допускает 1–2 ошибки, которые сам же исправляет. Оценка «3» ставится, если обучающийся обнаруживает знание и понимание основных положений данной темы, но излагает материал неполно и допускает неточности в определении понятий или формулировке правил. Оценка «2» ставится, если обучающийся обнаруживает незнание большей части соответствующего вопроса, допускает ошибки в формулировке определений и правил, искажающие их смысл, беспорядочно и неуверенно излагает материал |
Письменная проверочная работа
| Письменная проверочная работа №7
| ||||
| Тема | Действия с векторами | |||
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы
| |||
| 1 вариант А1. Изобразите на рисунке взаимное расположение точек А, В и С, если: а) А2. ABCDA1B1C1D1 – параллелепипед. Медианы треугольника ВB1С пересекаются в точке М. Разложите вектор А3. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. При каком значении k справедливо соотношение ___________________________________ В1. В кубе ABCDA1B1C1D1 точки Е и F – середины отрезков BD и C1С. Докажите, что прямые ВC1, ЕF и DC параллельны одной плоскости.
| 2 вариант
А1. Изобразите на рисунке взаимное расположение точек А, В и С, если:
а) 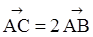 ; б) ; б)  ; в) ; в)  .
А2. М – середина стороны АВ параллелограмма ABCD, О – произвольная точка пространства. Разложите вектор .
А2. М – середина стороны АВ параллелограмма ABCD, О – произвольная точка пространства. Разложите вектор  по векторам по векторам  .
А3. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. При каком значении k справедливо соотношение .
А3. Диагонали параллелепипеда ABCDA1B1C1D1 пересекаются в точке О. При каком значении k справедливо соотношение  ?
___________________________________
В1. В тетраэдре ABCD точки М и Н – середины отрезков АD и ВС. Докажите, что прямые АВ, НМ и DC параллельны одной плоскости. ?
___________________________________
В1. В тетраэдре ABCD точки М и Н – середины отрезков АD и ВС. Докажите, что прямые АВ, НМ и DC параллельны одной плоскости.
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Практическое занятие
| Практическое занятие №5 | ||||
| Тема | Изучение скалярного произведения векторов, векторного уравнения прямой и плоскости. Использование векторов при доказательстве теорем стереометрии | |||
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |||
| 1 вариант 1. Дан квадрат ABCD. Найдите угол между векторами 𝐴 𝐶 ⃗ и 𝐷 𝐴 ⃗. 2. Найдите скалярный квадрат вектора с⃗ = 7𝑖 ⃗. 3. Найдите скалярное произведение 𝑎 ⃗ ∙ 𝑏, ⃗ если |𝑎 ⃗ |=3, |𝑏 ⃗ |=14, (𝑎 ⃗ ̂ 𝑏 ⃗ )= 60˚.
4. Вычислите скалярное произведение векторов 𝑎 ⃗ ∙ 𝑏, ⃗ если 𝑎 ⃗ {4; − 2; 3} 𝑏 ⃗ {− 1; − 2; 5}. 5. ABCDA1B1C1D1 - куб, ребро которого равно 1. Найдите скалярное произведение векторов 𝐴 𝐷 ⃗ 1 и 𝐵 𝐶 ⃗. 6. Вычислите угол между прямыми АВ и CD, если А(√ 3; 1; 0), С( 0; 2; 0 ), В(0; 0; 2√ 2 ), D(√ 3; 1; 2√ 2 ). 7. ABCDA1B1C1D1 - куб, ребро которого равно 1. Найдите скалярное произведение векторов 𝐵 𝐴 ⃗ 1 и 𝐶 𝐷 ⃗. 8. Вычислите угол между прямыми АВ и CD, если А(6; -4; 8), С(12; -6; 4), В(8; -2; 4), D(14; − 6; 2). | 2 вариант 1. Дан квадрат ABCD. Найдите угол между векторами 𝐵 𝐷 ⃗ и 𝐶 𝐵 ⃗. 2. Найдите скалярный квадрат вектора 𝑑 ⃗ = 5𝑖 ⃗ +2𝑘 ⃗. 3. Найдите скалярное произведение 𝑎 ⃗ ∙ 𝑏, ⃗ если |𝑎 ⃗ |=8, |𝑏 ⃗ |=5, (𝑎 ⃗ ̂ 𝑏 ⃗ )= 150˚. 4. Вычислите скалярное произведение векторов 𝑎 ⃗ ∙ 𝑏, ⃗ если 𝑎 ⃗ =2𝑖 ⃗ - 3𝑗 ⃗ +𝑘 ⃗ и 𝑏 ⃗ = 4𝑖 ⃗ - 𝑗 ⃗. 5. ABCDA1B1C1D1 - куб, ребро которого равно 2. Найдите скалярное произведение векторов 𝐴 𝐵 ⃗ 1 и 𝐷 𝐶 ⃗. 6. Вычислите угол между прямыми АВ и CD, если А(1; 1; 5 ), С(8; 5; 5 ), В(4; 7; 5), D(5; − 1; 5). 7. ABCDA1B1C1D1 - куб, ребро которого равно 3. Найдите скалярное произведение векторов 𝐵 𝐴 ⃗ 1 и 𝐵 𝐶 ⃗ 1. 8. Вычислите угол между прямыми АВ и CD, если А(-6; -15; 7), С(14; -10; 9), В(-7; -15; 8), D(14; -10; 7). | |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Контрольная точка
| Контрольная точка № 3 | ||||
| Тема | ДСК. Координаты и векторы в пространстве | |||
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы.
| |||
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |||
| 1 вариант 1. Даны точки А (3; – 1; 2) и В (5; 1; 1). Найдите: а) координаты вектора 2. Даны векторы а) координаты вектора 2 б) при каком значении у и z вектор 3. Найдите скалярное произведение векторов а) 4. Найдите значение m, при котором векторы 5. Найдите cos Ð j между векторами 6. Даны векторы а) Будут ли коллинеарными векторы б) Вычислите 7. А(1; 6; –3), В(–5; 3; –5), С(3; –1; 1). а) Найдите координаты вершины D параллелограмма ABCD. б) На оси аппликат найдите точку, равноудаленную от точек В и С. 8. Докажите, что ABCD — прямоугольник, если А(4; –2; 2), В(6; 1; –4), С(0; –1; –7), D(–2; –4; –1).
| 2 вариант
1. Даны точки А (3; – 1; 2) и В (5; 1; 1). Найдите:
а) координаты вектора  ; б) ; б) 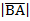 .
2. Даны векторы .
2. Даны векторы  (– 2; 3; 1) и (– 2; 3; 1) и  (4; – 1; 2). Найдите:
а) координаты вектора (4; – 1; 2). Найдите:
а) координаты вектора  + 3 + 3  ;
б) при каком значении у и z вектор ;
б) при каком значении у и z вектор  (8; у; z) и вектор (8; у; z) и вектор  коллинеарны?
3. Найдите скалярное произведение векторов коллинеарны?
3. Найдите скалярное произведение векторов  и и  , если:
а) , если:
а)  (– 2; 3; 1), (– 2; 3; 1),  (– 1; – 1; 4); б) (– 1; – 1; 4); б)  =2, =2, 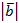 = 5, cos = 5, cos 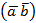 = 0, 1.
4. Найдите значение m, при котором векторы = 0, 1.
4. Найдите значение m, при котором векторы  и и  перпендикулярны, если перпендикулярны, если  (3; 2; – 1), (3; 2; – 1),
 (2; m; – 2).
5. Найдите cos Ð j между векторами (2; m; – 2).
5. Найдите cos Ð j между векторами  (3; 2; – 1) и (3; 2; – 1) и  (– 1; 2; 3).
6. Даны векторы (– 1; 2; 3).
6. Даны векторы  {2; –5; –4}, {2; –5; –4},  {–2; 2; –4}.
а) Будут ли коллинеарными векторы {–2; 2; –4}.
а) Будут ли коллинеарными векторы  и и 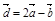 ?
б) Вычислите ?
б) Вычислите  .
7. А(1; 5; –2), В(–5; 4; –5), С(1; –4; 1).
а) Найдите координаты вершины D параллелограмма ABCD.
б) На оси абсцисс найдите точку, равноудаленную от точек В и С.
8. Докажите, что ABCD — квадрат, если А(–3; –4; 5), В(–2; 0; –3), С(2; 7; 1), D(1; 3; 9). .
7. А(1; 5; –2), В(–5; 4; –5), С(1; –4; 1).
а) Найдите координаты вершины D параллелограмма ABCD.
б) На оси абсцисс найдите точку, равноудаленную от точек В и С.
8. Докажите, что ABCD — квадрат, если А(–3; –4; 5), В(–2; 0; –3), С(2; 7; 1), D(1; 3; 9).
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки |
|
Раздел Основы тригонометрии | |||
| Тема 14. Основные понятия тригонометрии | ЛРN1, 2 МРN1, 4 ПРN1, 2 | Изучение радианного метода измерения углов вращения и их связи с градусной мерой. Изображение углов вращения на окружности, соотнесение величины угла с его расположением. Формулирование определений тригонометрических функций для углов поворота и острых углов прямоугольного треугольника и объяснение их взаимосвязи | Сообщение Устный опрос Письменная проверочная работа |
| Тема 15. Основные тригонометрические тождества | ЛРN2, 3 МРN2, 3 ПРN3 | Применение основных тригонометрических тождеств для вычисления значений тригонометрических функций по одной из них | Устный опрос Письменная проверочная работа |
| Тема 16. Преобразования простейших тригонометрических выражений | ЛРN5 МРN2, 4 ПРN3 | Изучение основных формул тригонометрии: формулы сложения, удвоения, преобразования суммы тригонометрических функций в произведение и произведения в сумму и применение при вычислении значения тригонометрического выражения и упрощения его. Ознакомление со свойствами симметрии точек на единичной окружности и применение их для вывода формул приведения | Письменная проверочная работа |
| Тема17. Тригонометрические уравнения и неравенства | ЛРN5 МРN2, 5 ПРN2, 4 | Решение по формулам и тригонометрическому кругу простейших тригонометрических уравнений и неравенств. Применение общих методов решения уравнений (приведение к линейному, квадратному, метод разложения на множители, замены переменной) при решении тригонометрических уравнений. Ознакомление с понятием обратных тригонометрических функций. Изучение определений арксинуса, арккосинуса, арктангенса числа, формулирование их, изображение на единичной окружности, применение при решении уравнений | Практическое занятие Контрольная точка №4 |
|
|
|
Сообщения
| Темы сообщений | Критерий оценивания |
| История тригонометрии. Тригонометрия вокруг нас. Использование тригонометрических функций в науках и практической жизни. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Устный опрос
| Вопросы для устного контроля по разделу | Критерии оценивания |
| 1. Дать определение синуса, косинуса, тангенса, котангенас произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа. 2. Основные тригонометрические тождества. 3. Формулы приведения. Синус, косинус и тангенс суммы и разности двух углов. Синус и косинус двойного угла. Формулы половинного угла. 4. Формулы решения простейших тригонометрических уравнений и неравенств. 5. Арксинус, арккосинус, арктангенс, арккотангенс. | Оценка «5» ставится, если обучающийся полно излагает материал (отвечает на вопрос), дает правильное определение основных понятий; обнаруживает понимание материала, может обосновать свои суждения, применить знания на практике . Оценка «4» ставится, если обучающийся дает ответ, удовлетворяющий тем же требованиям, что и для оценки «отлично», но допускает 1–2 ошибки, которые сам же исправляет. Оценка «3» ставится, если обучающийся обнаруживает знание и понимание основных положений данной темы, но излагает материал неполно и допускает неточности в определении понятий или формулировке правил. Оценка «2» ставится, если обучающийся обнаруживает незнание большей части соответствующего вопроса, допускает ошибки в формулировке определений и правил, искажающие их смысл, беспорядочно и неуверенно излагает материал |
Письменная проверочная работа
| Письменная проверочная работа № 8
| |
| Тема | Тригонометрические выражения |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы |
| 1 вариант 1. Вычислите 2. Найдите значение выражения 3. Вычислите значение каждой из тригонометрических функций, если
| |
| 2 вариант 1. Вычислите 2. Найдите значение выражения 3. Вычислите значение каждой из тригонометрических функций, если
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % |
Письменная проверочная работа
| Письменная проверочная работа №9
| |
| Тема | Тригонометрические преобразования |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы |
| 1 вариант
| |
| 2 вариант
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % |
Письменная проверочная работа
| Письменная проверочная работа №10
| ||
| Тема | Тригонометрические преобразования: формулы приведения | |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы | |
| 1 вариант А1. Вычислите А2. Упростите выражение
А3. Упростите выражение
В1. Найдите значение выражения
| 2 вариант
А1Вычислите  А2. Упростите выражение
А2. Упростите выражение  А3. Упростите выражение
А3. Упростите выражение  В1. Найдите значение выражения
В1. Найдите значение выражения  , если , если 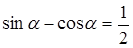 . .
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
|
|
|



 ; б)
; б)  ; в)
; в) 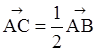 .
.  по векторам
по векторам 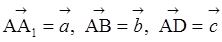 .
. 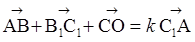 ?
? 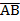 ; б)
; б)  .
.  .
.  и
и  ?
? 

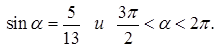
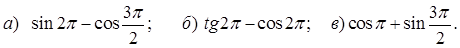


 .
. 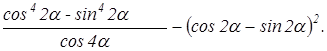
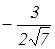 , α
, α 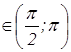 .
. 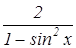 , если tg x = 4.
, если tg x = 4. 



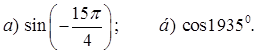


 , если
, если  .
.