 |
2.3 Оценка результатов обучения при проведении промежуточной аттестации по учебному предмету 6 страница
|
|
|
|
| Письменная проверочная работа №12
| ||
| Тема | Правила дифференцирования | |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы | |
| 1 вариант 1. Найти производную функции 1) 2) 3) 4) 5) 6) 2. Найти х, при которых f(x)= (5х-7)/(4х+3) | 2 вариант
1. Найти производную функции
1)  ,
2) ,
2) 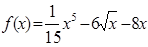 ,
3) ,
3) 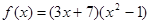 4)
4)  5)
5) 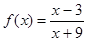 ,
6) ,
6) 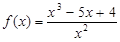 2. Найти х, при которых
2. Найти х, при которых  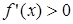 f(x)=
f(x)= 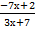
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Практическое занятие
| Практическое занятие №15 | ||||
| Тема | Составление уравнения касательной к графику функции | |||
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы | |||
| Правила вычисления производных Вариант 1 А1. Найдите производную функции: а) х5+2х; б) 12х6 - 45; в) А2. Найдите производную функции а) (х2 -3)(х+х3); б)
А3. При каких значениях х значение производной функции f(x = х5+2, 5х4-12 равно 0?
В1. Найдите значения х, при которых значение производной функции В2. Найдите производную функции
C1. При каких значениях х производная функции Касательная к графику функции Вариант 1 А1. Найдите тангенс угла наклона касательной к графику функции А2. Найдите угловой коэффициент касательной, проведенной к графику функции
В1. На рисунке изображен график функции и касательная к нему в точке с абсциссой Чему равна производная данной функции в этой точке?
| Правила вычисления производных
Вариант 2
А1. Найдите производную функции:
а) 3х5-2х2; б) 2х5 - 5; в)  ; г) 32 ; г) 32  .
А2. Найдите производную функции а) (х3 +3)(х-х3); б) .
А2. Найдите производную функции а) (х3 +3)(х-х3); б)  .
А3. При каких значениях х значение производной функции f(x = х3-12х-32 равно 0?
В1. Найдите значения х, при которых значение производной функции .
А3. При каких значениях х значение производной функции f(x = х3-12х-32 равно 0?
В1. Найдите значения х, при которых значение производной функции  положительно.
В2. Найдите производную функции положительно.
В2. Найдите производную функции  .
C1. При каких значениях х производная функции .
C1. При каких значениях х производная функции 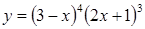 принимает отрицательные значения?
Касательная к графику функции
Вариант 2
А1. Найдите тангенс угла наклона касательной к графику функции принимает отрицательные значения?
Касательная к графику функции
Вариант 2
А1. Найдите тангенс угла наклона касательной к графику функции  в точке с абсциссой в точке с абсциссой  .
А2. Найдите угловой коэффициент касательной, проведенной к графику функции .
А2. Найдите угловой коэффициент касательной, проведенной к графику функции 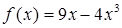 в точке с абсциссой в точке с абсциссой  .
А3. Напишите уравнение касательной к графику функции .
А3. Напишите уравнение касательной к графику функции  в точке с абсциссой в точке с абсциссой 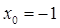 . .
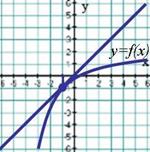 В1. На рисунке изображен график функции
В1. На рисунке изображен график функции 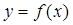 и касательная к нему в точке с абсциссой
и касательная к нему в точке с абсциссой 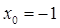 .
Чему равна производная данной функции в этой точке? .
Чему равна производная данной функции в этой точке?
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Практическое занятие
| Практическое занятие №16 | ||
| Тема | Исследование функций с помощью производной | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| 1 вариант А1. Исследуйте функцию и постройте ее график. а)у= х3 - 4х, б) у=2 + в) у= 6 - 2, 5х – 0, 5 х3 В1. Исследуйте функцию
В2. Найдите наименьшее и наибольшее значения функции
С1. Сколько корней имеет уравнение
| 2 вариант
А1. Исследуйте функцию и постройте ее график.
а)у= х3 +3 х, б) у=1 +  в) у= 4 - 3, 5х + 0, 5 х3
В1. Исследуйте функцию
в) у= 4 - 3, 5х + 0, 5 х3
В1. Исследуйте функцию  и постройте ее график.
В2. Найдите наименьшее и наибольшее значения функции и постройте ее график.
В2. Найдите наименьшее и наибольшее значения функции  на отрезке на отрезке  .
С1. Сколько корней имеет уравнение .
С1. Сколько корней имеет уравнение 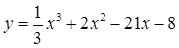 ? ?
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. | |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Контрольная точка
| Контрольная точка №7 | ||||
| Тема | Производная функции и ее применение | |||
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы.
| |||
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |||
| 1 вариант А1. Найти производную функции: а) у=3х3 –5х2 +х +4; б) у= в) у=12х + sin x; г )у= А2. Найти значение производной функции А3. Найдите угловой коэффициент касательной к графику функции f(x) = 4ех в точке с абсциссой х0 = 0.
В1. При каких значениях х, производная функции В2. Напишите уравнение касательной к графику функции f(x) = (2x-1)3 в точке с абсциссой х0 = 1. В3. При каких значениях х, производная функции f(x) = ln3x -3x положительна? С1. В каких точках касательная к графику функции у = sin х образует угол с осью Ох, равный 450? C2. Напишите уравнение касательной к графику функции f(x) = 2x2 –3x, если касательная параллельна прямой у = х –3. | 2 вариант
А1. Найти производную функции:
а) у=5х4 –15х2 +4;
б) у=  в) у=2х + 3sin 2x;
г) у=
в) у=2х + 3sin 2x;
г) у= 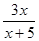 .
А2. Найти значение производной функции .
А2. Найти значение производной функции 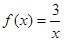 в точке х0 = в точке х0 = 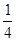 .
А3. Найдите угловой коэффициент касательной к графику
функции f(x) = 4ех -2 в точке с абсциссой
х0 = 2.
В1. При каких значениях х, производная функции у = -х4 +4х2 -5 равна 0?
В2. Напишите уравнение касательной к графику функции f(x) = е1-х точке с абсциссой х0 = 1.
В3. При каких значениях х, производная функции f(x) =1 + .
А3. Найдите угловой коэффициент касательной к графику
функции f(x) = 4ех -2 в точке с абсциссой
х0 = 2.
В1. При каких значениях х, производная функции у = -х4 +4х2 -5 равна 0?
В2. Напишите уравнение касательной к графику функции f(x) = е1-х точке с абсциссой х0 = 1.
В3. При каких значениях х, производная функции f(x) =1 + 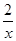 положительна?
С1. В каких точках касательная к графику функции у = cos х образует угол с осью Ох, равный 450?
C2. Прямая у = 4х –3 является касательной к параболе f(x) = 6 – 2х + х2. Найти координаты точки касания. положительна?
С1. В каких точках касательная к графику функции у = cos х образует угол с осью Ох, равный 450?
C2. Прямая у = 4х –3 является касательной к параболе f(x) = 6 – 2х + х2. Найти координаты точки касания.
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении. | |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки | ||
|
Раздел Интеграл и его применение
| |||||
| Тема 26 Первообразная и интеграл | ЛРN1, 2 МРN1, 4 ПРN2, 5 | Ознакомление с понятием интеграла и первообразной. Изучение правила вычисления первообразной и теоремы Ньютона— Лейбница. Решение задач на связь первообразной и ее производной, вычисление первообразной для данной функции. | Сообщение Письменная проверочная работа | ||
| Тема 27. Применение интеграла | ЛРN2, 7 МРN1, 5 ПРN2, 5 | Решение задач на применение интеграла для вычисления физических величин и площадей | Контрольная точка №8 | ||
Сообщения
| Темы сообщений | Критерий оценивания |
| История интегрального исчисления. Интеграл и его применение в жизни человека. Приложения определенного интеграла в геометрии. Приложения определенного интеграла в физике. Приложения определенного интеграла в экономике. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Письменная проверочная работа
| Письменная проверочная работа № 13
| ||||
| Тема | Правила нахождения первообразных | |||
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы
| |||
| А1. Найдите общий вид первообразных для функции f : А2. Для функции через точку В1. Скорость прямолинейно движущейся точки задана формулой
| А1. Найдите общий вид первообразных для функции f:
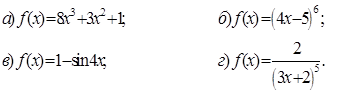 А2. Для функции
А2. Для функции  найдите первообразную, график которой проходит
через точку найдите первообразную, график которой проходит
через точку  .
В1. Скорость прямолинейно движущейся точки задана формулой .
В1. Скорость прямолинейно движущейся точки задана формулой  . Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат. . Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат.
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Контрольная точка
| Контрольная точка №8 | ||
| Тема | Интеграл | |
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. | |
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |
| 1 вариант А1. Для функции f(х) = 3х2+1 найти первообразную, график которой проходит через точку М(1; -2).
А2. Вычислите интеграл: 1) В1. Найти площадь фигуры, ограниченной линиями у = 6х –х2 и у = х+4. В2. Найти площадь фигуры, ограниченной линиями у = х2 +1 и у = 3 –х. С1. Построить графики функций и вычислить площадь фигуры, ограниченной этими линиями: у= С2. Найти площадь фигуры, ограниченной линиями у =
| 2 вариант
А1. Для функции f(х) = ех найти первообразную, график которой проходит через точку М(0; 2).
А2. Вычислите интеграл:
1) 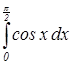 ; 2) ; 2)  ;
3) ;
3) 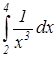 .
В1. Найти площадь фигуры, ограниченной прямой у = -6х и параболой у= -12х -3х2.
В2. Найти площадь фигуры, ограниченной линиями у = х2 -1 и у = 1–х.
С1. Построить графики функций и вычислить площадь фигуры, ограниченной этими линиями: у = х3 и у= .
В1. Найти площадь фигуры, ограниченной прямой у = -6х и параболой у= -12х -3х2.
В2. Найти площадь фигуры, ограниченной линиями у = х2 -1 и у = 1–х.
С1. Построить графики функций и вычислить площадь фигуры, ограниченной этими линиями: у = х3 и у=  .
С2. Найти площадь фигуры, ограниченной линиями
у = cosx, у = 0, х = .
С2. Найти площадь фигуры, ограниченной линиями
у = cosx, у = 0, х =  и х = и х =  . .
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
|
Раздел Элементы теории вероятностей и математической статистики | |||
| Тема 28 Основы теории вероятностей | ЛРN2, 6 МРN1, 6 ПРN1, 7 | Изучение классического определения вероятности, свойств вероятности, теоремы о сумме вероятностей. Рассмотрение примеров вычисления вероятностей. Решение задач на вычисление вероятностей событий | Сообщение Практическое занятие |
| Тема 29 Основы математической статистики | ЛРN2, 6 МРN1, 6 ПРN1, 7 | Ознакомление с представлением числовых данных и их характеристиками. Решение практических задач на обработку числовых данных, вычисление их характеристик | Контрольная точка №9 |
Сообщения
| Темы сообщений | Критерий оценивания |
| Случайные величины вокруг нас и их числовые характеристики. Случайные события и вероятность События и вероятности Счастливый билет Теория вероятностей в азартных играх Теория вероятностей в игре Теория вероятностей и статистика Частота и вероятность. Частота в статистике и решении экономических. задач Средние значения и их применение в статистике. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Практическое занятие
| Практическое занятие №17 | ||||||||||
| Тема | Решение практических задач с применением вероятностных методов | |||||||||
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |||||||||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |||||||||
| 1 вариант Решить задачи: 1. В группе туристов 5 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Турист А. хотел бы сходить в магазин, но он подчиняется жребию. Какова вероятность того, что А. пойдёт в магазин? 2. Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза. 3. Игральный кубик бросают дважды. Сколько элементарных исходов опыта благоприятствуют событию «А = сумма очков равна 5»? 4. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что в первый раз выпадает орёл, а во второй — решка. 5. На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых. 6. В некотором городе из 5000 появившихся на свет младенцев 2512 мальчиков. Найдите частоту рождения девочек в этом городе. Результат округлите до тысячных. 7. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир В. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру В. достанется удобное место, если всего в самолёте 300 мест. Статистика Вариант 1
1. В ходе опроса 40 учащихся школы было выяснено, сколько времени (с точностью до 0, 5 ч) в неделю они затрачивают на занятия в кружках и спортивных секциях. Получили следующие данные: 2, 2, 5, 5, 1, 5, 4, 3, 1, 5, 3, 5, 4, 3, 3, 5, 2, 5, 3, 1, 5, 4, 5, 3, 5, 4, 3, 5, 2, 5, 2, 4, 0, 2, 5, 0, 5, 3, 5, 2, 3, 5, 3, 2, 5, 5, 1, 5, 3, 5, 2, 5, 4, 5, 2, 5, 3, 5, 1, 3, 5, 1, 1, 5. а) Составьте сгруппированный ряд этих данных. б) Чему равна мода этого измерения и какова ее кратность? в) Выпишите таблицу распределения данных. г) Найдите среднее значение времени, затрачиваемое учащимися на занятие в кружках.
2. Учащиеся одиннадцатых классов некоторого города сдавали пробный экзамен по алгебре. Итоги этого экзамена представили в таблице:
Составьте гистограмму распределения данных.
| 2 вариант
Решить задачи
1. В группе туристов 30 человек. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 6 человек за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист П. полетит первым рейсом вертолёта.
2. Вероятность того, что новый DVD-проигрыватель в течение года поступит в гарантийный ремонт, равна 0, 045. В некотором городе из 1000 проданных DVD-проигрывателей в течение года в гарантийную мастерскую поступила 51 штука. На сколько отличается частота события «гарантийный ремонт» от его вероятности в этом городе?
3. В кармане у Миши было четыре конфеты — «Грильяж», «Белочка», «Коровка» и «Ласточка», а также ключи от квартиры. Вынимая ключи, Миша случайно выронил из кармана одну конфету. Найдите вероятность того, что потерялась конфета «Грильяж».
4. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 10, но не дойдя до отметки 1 час.
5. Из множества натуральных чисел от 25 до 39 наудачу выбирают одно число. Какова вероятность того, что оно делится на 5?
6. В чемпионате по прыжкам в воду участвуют 35 спортсменов: 7 из России, 12 из Китая, 9 из Японии и 7 из США. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий первым, окажется представителем России.
7. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с вишней. Петя выбирает наугад один пирожок. Найдите вероятность того, что этот пирожок окажется с вишней.
Статистика
Вариант 2
1. В ходе опроса 30 учащихся школы было выяснено, сколько времени (с точностью до 0, 5 ч) в неделю они затрачивают на занятия с компьютером. Получили следующие данные: 3, 2, 5, 5, 5, 3, 5, 4, 3, 6, 2, 5, 2, 5, 4, 5, 6, 5, 4, 3, 4, 5, 3, 5, 4, 5, 5, 5, 2, 4, 3, 3, 5, 2, 5, 4, 5, 4, 3, 5, 2, 2, 5, 5.
а) Составьте сгруппированный ряд этих данных.
б) Чему равна мода этого измерения и какова ее кратность?
в) Выпишите таблицу распределения данных.
г) Найдите среднее значение времени, затрачиваемое учащимися на занятие в кружках.
2. Учащиеся одиннадцатых классов некоторого города выполняли контрольную работу по алгебре. Итоги этой работы представили в таблице, в которой указали число учащихся, верно выполнивших одно, два, три и т. д. задания:
Составьте гистограмму распределения данных. | |||||||||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||||||||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||||||||
Контрольная точка
|
|
|



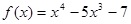 ,
, 
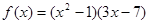
 ,
,  ,
, 
 ; г) 32
; г) 32 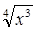 .
. 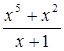 .
.  положительно.
положительно. 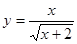 .
.  принимает отрицательные значения?
принимает отрицательные значения?  в точке с абсциссой
в точке с абсциссой 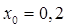 .
. 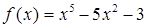 в точке с абсциссой
в точке с абсциссой 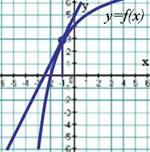 А3. Напишите уравнение касательной к графику функции
А3. Напишите уравнение касательной к графику функции  в точке с абсциссой
в точке с абсциссой 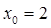 .
. 
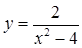 и постройте ее график.
и постройте ее график.  на отрезке
на отрезке  ?
?  ;
; 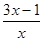 .
. 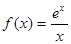 в точке х0 = 1.
в точке х0 = 1. 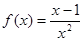 равна 0?
равна 0? 
 найдите первообразную, график которой проходит
найдите первообразную, график которой проходит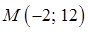 .
.  . Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат.
. Запишите формулу зависимости ее координаты х от времени t, если известно, что в начальный момент времени (t=0) точка находилась в начале координат. 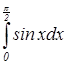 ; 2)
; 2)  ; 3)
; 3)  .
. 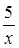 и у=6 - х.
и у=6 - х.