 |
2.3 Оценка результатов обучения при проведении промежуточной аттестации по учебному предмету 4 страница
|
|
|
|
Практическое занятие
| Практическое занятие №6 | ||
| Тема | Решение тригонометрических уравнений | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| 1 вариант А1. Решите уравнение: а) б) А2. Решите уравнение:
В1. Решите уравнение В2. Решите уравнение В3. Решите уравнение В4. Решите уравнение С1. Сколько нецелых корней имеет уравнение
| 2 вариант
А1. Решите уравнение:
а)  ;
б) ;
б) 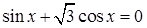 .
А2. Решите уравнение: .
А2. Решите уравнение: 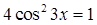 .
В1. Решите уравнение .
В1. Решите уравнение
 В2. Решите уравнение
В2. Решите уравнение 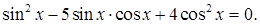 В3. Решите уравнение
В3. Решите уравнение  В4. Решите уравнение
В4. Решите уравнение  С1. Сколько корней имеет уравнение
С1. Сколько корней имеет уравнение  . .
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Практическое занятие
| Практическое занятие №7 | ||||
| Тема | Решение простейших тригонометрических неравенств | |||
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |||
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |||
| 1 вариант А1. Вычислите
А2. Решите неравенства 1) 2 sinx < 1, 2) cos 4x > 0, 3) -2sin 2x < 4) -tg(2x – п/6) < 5) sinx > cosx, 6) 3 – 4cos2x > 0, 7) cos2x+5cosx+3 Дополнительно: В1. Решите уравнение В2. Решите уравнение | 2 вариант
А1. Вычислите 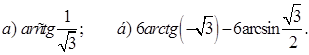 А2. Решите неравенства
1) 2 cosx > – 1,
2) sin 2x < 0,
3) 2cos 3x >
А2. Решите неравенства
1) 2 cosx > – 1,
2) sin 2x < 0,
3) 2cos 3x >  ,
4) tg(3x + п/3) > ,
4) tg(3x + п/3) >  ,
5) sinx < cosx,
6) 1 – 4sin2 x < 0,
7) 2sin2x+3sinx–2 ,
5) sinx < cosx,
6) 1 – 4sin2 x < 0,
7) 2sin2x+3sinx–2  0,
Дополнительно:
В1. Решите уравнение 0,
Дополнительно:
В1. Решите уравнение 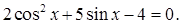 В2. Решите уравнение
В2. Решите уравнение  . .
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
Контрольная точка
| Контрольная точка № 4 | ||||
| Тема | Тригонометрические функции числового аргумента | |||
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. | |||
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |||
| 1 вариант А1. Вычислите а) А2. Найдите значение выражения 2сtg α = А3. Упростите выражение А4. Найдите значение выражения cos А5. Решите уравнение: а) б)
А6. Решите уравнение: а) б) В1. Решите уравнение В2. Решите уравнение С1. Решите уравнение | 2 вариант
А1. Вычислите а)  ; б) cos 3660o.
А2. Найдите значение выражения
sinα ·cos ; б) cos 3660o.
А2. Найдите значение выражения
sinα ·cos  -2sin -2sin  +
cosα ·sin +
cosα ·sin  при α = при α =  .
А3. Упростите выражение .
А3. Упростите выражение 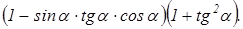 А4. Найдите значение выражения
cos
А4. Найдите значение выражения
cos  - sin - sin 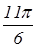 .
А5. Решите уравнение:
а) .
А5. Решите уравнение:
а)  ;
б) ;
б) 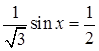 .
А6. Решите уравнение:
а) .
А6. Решите уравнение:
а)  ;
б) ;
б) 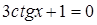 .
В1. Решите уравнение .
В1. Решите уравнение  В2. Решите уравнение
В2. Решите уравнение  С1. Решите уравнение
С1. Решите уравнение 
| |||
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |||
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |||
| Название раздела/темы занятия | КодЛРN МРN ПРN | Результаты обучения (на уровне учебных действий) | Методы оценки |
|
Раздел Функции и графики | |||
| Тема18. Функции их свойства и графики. | ЛРN2, 3 МРN1, 6 ПРN1, 2 | Ознакомление с примерами функциональных зависимостей в реальных процессах из смежных дисциплин. Ознакомление с доказательными рассуждениями некоторых свойств линейной и квадратичной функций, проведение исследования линейной, кусочно-линейной, дробно-линейной и квадратичной функций, построение их графиков. Построение и чтение графиков функций. Исследование функции. Составление видов функций по данному условию, решение задач на экстремум. Выполнение преобразований графика функции | Устный опрос Сообщение Практическое занятие |
| Тема 19. Степенная, показа- тельная, логарифми- ческая и тригономе- трические функции. | ЛРN1, 2 МРN2, 4 ПРN2, 4 | Вычисление значений функций по значению аргумента. Определение положения точки на графике по ее координатам и наоборот. Использование свойств функций для сравнения значений степеней и логарифмов. Построение графиков степенных и логарифмических функций. Решение показательных и логарифмических уравнений и неравенств по известным алгоритмам. Ознакомление с понятием непрерывной периодической функции, формулирование свойств синуса и косинуса, построение их графиков. Ознакомление с понятием гармонических колебаний и примерами гармонических колебаний для описания процессов в физике и других областях знания. Ознакомление с понятием разрывной периодической функции, формулирование свойств тангенса и котангенса, построение их графиков. Применение свойств функций для сравнения значений тригонометрических функций, решения тригонометрических уравнений. Выполнение преобразования графиков функций | Устный опрос Практическое занятие Контрольная точка №5 |
| Тема 20. Обратные функции. Обратные тригонометрические функции | ЛРN5, 6 МРN3, 5 ПРN2, 4 | Изучение понятия обратной функции, определение вида и построение графика обратной функции, нахождение ее области определения и области значений. Построение графиков обратных тригонометрических функций и определение по графикам их свойств. Применение свойств функций при исследовании уравнений и решении задач на экстремум. Ознакомление с понятием сложной функции | Письменная проверочная работа |
|
|
|
Сообщения
| Темы сообщений | Критерий оценивания |
| Исторические сюжеты о функциях. История развития понятия функции. Функции в окружающем нас мире. Функции в жизни человека. Использование функций в науках и практической жизни. | Оценка «отлично»- учебный материал освоен студентом в полном объеме, легко ориентируется в материале, полно и аргументировано отвечает на дополнительные вопросы, излагает материал логически последовательно, делает самостоятельные выводы, умозаключения, демонстрирует кругозор, использует материал из дополнительных источников, интернет ресурсы. Сообщение носит исследовательский характер. Речь характеризуется эмоциональной выразительностью, четкой дикцией, стилистической и орфоэпической грамотностью. Использует наглядный материал (презентация). Оценка «хорошо»- по своим характеристикам сообщение студента соответствует характеристикам отличного ответа, но студент может испытывать некоторые затруднения в ответах на дополнительные вопросы, допускать некоторые погрешности в речи. Отсутствует исследовательский компонент в сообщении. Оценка «удовлетворительно»- студент испытывал трудности в подборе материала, его структурировании. Пользовался, в основном, учебной литературой, не использовал дополнительные источники информации. Не может ответить на дополнительные вопросы по теме сообщения. Материал излагает не последовательно, не устанавливает логические связи, затрудняется в формулировке выводов. Допускает стилистические и орфоэпические ошибки. Оценка «неудовлетворительно»- сообщение студентом не подготовлено либо подготовлено по одному источнику информации, либо не соответствует теме. |
Устный опрос
|
|
|
| Вопросы для устного контроля по разделу | Критерии оценивания |
| 1. Определение функции. Область определения и множество значений. 2. Что называют графиком функции. 3. Правила построения графиков функций, заданных различными способами. 4 Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. 5. Раскрыть понятие сложной функции (композиция функций). 6. Взаимно обратные функции. Область определения и область значений обратной функции. График обратной функции. | Оценка «5» ставится, если обучающийся полно излагает материал (отвечает на вопрос), дает правильное определение основных понятий; обнаруживает понимание материала, может обосновать свои суждения, применить знания на практике . Оценка «4» ставится, если обучающийся дает ответ, удовлетворяющий тем же требованиям, что и для оценки «отлично», но допускает 1–2 ошибки, которые сам же исправляет. Оценка «3» ставится, если обучающийся обнаруживает знание и понимание основных положений данной темы, но излагает материал неполно и допускает неточности в определении понятий или формулировке правил. Оценка «2» ставится, если обучающийся обнаруживает незнание большей части соответствующего вопроса, допускает ошибки в формулировке определений и правил, искажающие их смысл, беспорядочно и неуверенно излагает материал |
Письменная проверочная работа
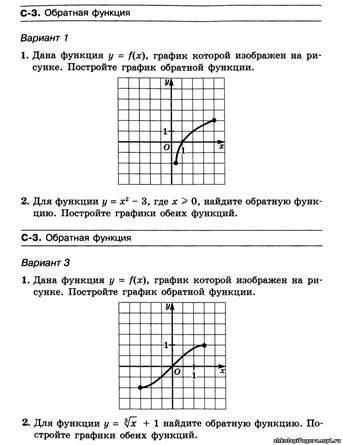
| Письменная проверочная работа № 11
| ||
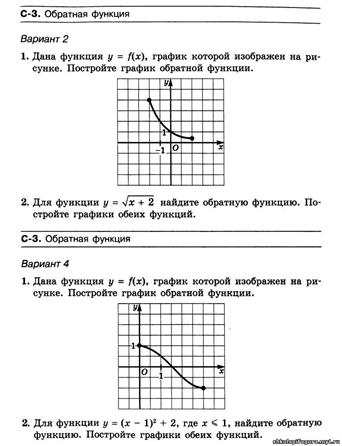
| Тема | Обратные функции и их свойства. | |
| Цель работы | закрепление практических навыков применения теоретических подходов и методов анализа на учебных примерах и задачах. | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для проверочной работы | |
|
| 
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
|
|
|
Практическое занятие
| Практическое занятие №8 | ||
| Тема | Построение графиков функций, заданных различными способами и определение монотонности, четности, нечетности функций | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| Вариант1 1. Построить графики функций, укажите их промежутки монотонности А) у= 5х-4 Б) у= В) ) у= 5х2- х + 4 Г ) у= 2. Найти Д (у) А) у=х4-3х2+12, Б) у= 3. Задана функция у= 3х3+х -16 Найти у (0), у(-2), у(7) 4. Проверить функцию на четность/ не четность А) у=х4-6х2-12 Б) у= | Вариант 2.
1. Построить графики функций, укажите их промежутки монотонности
А)у= -2х+4 Б)у=  В) ) у= 3х2+ х - 2 Г ) у=
В) ) у= 3х2+ х - 2 Г ) у=  2. Найти Д (у)
А) у=х4-6х2-12, Б) ) у=
2. Найти Д (у)
А) у=х4-6х2-12, Б) ) у= 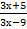 , В) у= , В) у=  3. Задана функция
у=4х3 -2х+13
Найти у (0), у(-3), у(8)
4. Проверить функцию на четность/ не четность
А) у=х5-3х7+12 Б) )у=
3. Задана функция
у=4х3 -2х+13
Найти у (0), у(-3), у(8)
4. Проверить функцию на четность/ не четность
А) у=х5-3х7+12 Б) )у= 
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Практическое занятие
| Практическое занятие №9 | ||
| Тема | Нахождение области определения и область значений функций | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| 1 вариант 1. Найти: Д(у), Е (у), у> 0, у< 0, у=0, промежутки возрастания и убывания, экстремумы
2 часть 1. Функция задана формулой f(x) = 2x2 - 3. Найдите произведение f(-1) ⋅ f(2). 2. Найдите область определения функции у = 3. Задана функция f(x) = -3x + 1, где -2 ≤ x ≤ 3. Найдите область значений функции. 4. Дана функция y = 3 - 2x. Найдите зависимость переменной x от величины y. 5. Высота подъема h (м) тела, брошенного вертикально вверх с начальной скоростью v0 (м/с), вычисляется по формуле h = v0/ 2g (g ≈ 10 м/c2). При какой скорости v0 высота подъема h = 20 (м)?
| 2 вариант
1. Найти: Д(у), Е (у), у> 0, у< 0, у=0, промежутки возрастания и убывания, экстремумы
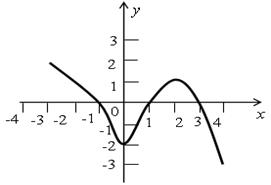
 2 часть
1. Функция задана формулой f(x) = 3x2 - 2. Найдите произведение
f(-2) ⋅ f(1).
2. Найдите область определения функции
У=
2 часть
1. Функция задана формулой f(x) = 3x2 - 2. Найдите произведение
f(-2) ⋅ f(1).
2. Найдите область определения функции
У= 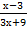 4. Задана функция f(x) = -2x + 3,
где -2 ≤ x ≤ 3. Найдите область
значений функции.
4. Дана функция y = 5 - 3x. Найдите зависимость переменной x
от величины y.
5. Высота подъема h (м) тела, брошенного вертикально вверх с начальной скоростью v0 (м/с), вычисляется по формуле h = v0/ 2g
(g ≈ 10 м/c2). При какой скорости v0 высота подъема h = 80 (м)?
4. Задана функция f(x) = -2x + 3,
где -2 ≤ x ≤ 3. Найдите область
значений функции.
4. Дана функция y = 5 - 3x. Найдите зависимость переменной x
от величины y.
5. Высота подъема h (м) тела, брошенного вертикально вверх с начальной скоростью v0 (м/с), вычисляется по формуле h = v0/ 2g
(g ≈ 10 м/c2). При какой скорости v0 высота подъема h = 80 (м)?
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Практическое занятие
| Практическое занятие №10 | ||
| Тема | Построение функций из нескольких композиций | |
| Цель работы | систематизация и закрепление полученных теоретических знаний и практических умений обучающихся по данной теме; углубление и расширение теоретических знаний по данной теме | |
| Дидактический материал | Рабочая тетрадь для практических занятий, конспект теоретического материала по данной теме, задания для самостоятельной работы
| |
| 1 вариант 1. Построить график функции
6. Построить график функции
Прочитать график функции 7. Построить график функции
При каких значениях c прямая y=c имеет с графиком функции ровно три общие точки? 4. На рисунке изображён график функции вида | 2 вариант
1. Построить график функции
 Найти промежутки возрастания и убывания функции.
2. Построить график функции Найти промежутки возрастания и убывания функции.
2. Построить график функции
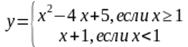 Прочитать график функции
3. Построить график функции
Прочитать график функции
3. Построить график функции
 При каких значениях а прямая y=а имеет с графиком функции ровно две общие точки?
8. На рисунке изображён график функции вида
При каких значениях а прямая y=а имеет с графиком функции ровно две общие точки?
8. На рисунке изображён график функции вида  где числа a, b, c и d — целые. Найдите корень уравнения где числа a, b, c и d — целые. Найдите корень уравнения 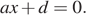

| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
Контрольная точка
| Контрольная точка №5 | ||
| Тема | Функции. Свойства функций | |
| Цель работы | использование основных алгоритмов для решения задач контрольной работы, умение анализировать условие задачи, сопоставлять его с изученными алгоритмами и выбирать из них необходимый, использовать математический язык для записи выполненных заданий, учиться контролировать качество выполнения работы, планировать и контролировать время на выполнение работы. | |
| Дидактический материал | Рабочая тетрадь для контрольных работ, задания для контрольной работы | |
| 1 вариант A1. Найдите область определения функций: а) A2. Выяснить, является ли функция чётной или нечётной: а)
а) область определения функции б) область значения функции в) нули функции г) наибольшее и наименьшее значение функции; д) промежутки возрастания и убывания функции.
A4. Графиком какой из указанных функций является гипербола: A5. Вычислите координаты точек пересечения графика функции
A6. Изобразите график непрерывной функции, зная, что: а) область определения функции промежуток [ − 4; 3]; б) значение функции составляет промежуток [− 3; 3]; в) промежутки возрастания функции [− 4; − 3] и [− 1; 3]; г) функция убывает [− 3; − 1]; д) нули функции: -3 и 1 B1. Найдите область определения функций: а) B2. Решите графически систему уравнений:
B3. Исследуйте функцию и постройте её график:
|  2 вариант
A1. Найдите область определения функций:
а) 2 вариант
A1. Найдите область определения функций:
а)  б) б)  A2. Выяснить, является ли функция чётной или нечётной:
а)
A2. Выяснить, является ли функция чётной или нечётной:
а)  ; б) ; б) 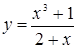 ;
A3. Функция ;
A3. Функция 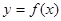 задана графиком на рисунке. Укажите:
а) область определения функции
б) область значения функции
в) нули функции
г) наибольшее и наименьшее значение функции;
д) промежутки возрастания и убывания функции.
A4. Графиком какой из указанных функций является парабола: задана графиком на рисунке. Укажите:
а) область определения функции
б) область значения функции
в) нули функции
г) наибольшее и наименьшее значение функции;
д) промежутки возрастания и убывания функции.
A4. Графиком какой из указанных функций является парабола: 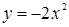 , ,  или или  ? Постройте эту параболу.
A5. Вычислите координаты точек пересечения графика функции ? Постройте эту параболу.
A5. Вычислите координаты точек пересечения графика функции
 с осью х.
A6. Изобразите график непрерывной функции, зная, что:
а) область определения функции промежуток [ − 5; 4];
б) значение функции составляет промежуток [− 2; 4];
в) промежутки возрастания функции [1; 3];
г) функция убывает [− 5; 1] и [3; 4];
д) нули функции: -2 и 2
B1. Найдите область определения функций:
а) с осью х.
A6. Изобразите график непрерывной функции, зная, что:
а) область определения функции промежуток [ − 5; 4];
б) значение функции составляет промежуток [− 2; 4];
в) промежутки возрастания функции [1; 3];
г) функция убывает [− 5; 1] и [3; 4];
д) нули функции: -2 и 2
B1. Найдите область определения функций:
а)  ;
б) ;
б)  ;
B2. Решите графически систему уравнений: ;
B2. Решите графически систему уравнений:
 B3. Исследуйте функцию и постройте её график:
B3. Исследуйте функцию и постройте её график:
 . При каких значениях х функция принимает отрицательные значения? . При каких значениях х функция принимает отрицательные значения?
| |
| Требования к отчету: | Отчет должен содержать развернутое решение заданий с указаниями на теоретические факты, использованные при решении.
| |
| Критерии оценки | «5» - процент результативности 91-100% (правильных ответов); «4» - процент результативности 75-90 %; «3» - процент результативности 60-74%; «2» - процент результативности менее 60 % | |
|
|
|



 ;
; 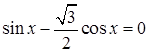 .
. 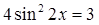 .
. 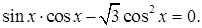
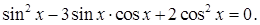


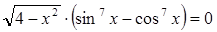 ?
? 
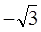 ,
, 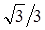 ,
,  0,
0, 
 .
. 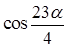 ; б) sin (-1560o).
; б) sin (-1560o).  ·tg
·tg 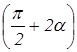 ·ctg4α при
·ctg4α при
 - sin
- sin  .
.  ;
; 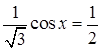 .
. 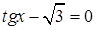 ;
;  .
. 
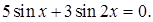


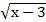
 , В)у=
, В)у= 


 Найти промежутки возрастания и убывания функции.
Найти промежутки возрастания и убывания функции. 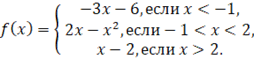

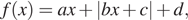 где числа a, b, c и d — целые. Найдите корень уравнения
где числа a, b, c и d — целые. Найдите корень уравнения 

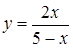 б)
б) 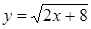
 ; б)
; б)  ;
;  A3. Функция
A3. Функция  ,
,  или
или 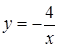 ? Постройте эту гиперболу.
? Постройте эту гиперболу. 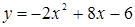 с осью х.
с осью х. 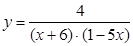 ; б)
; б) 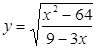 ;
; 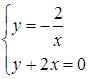
 . При каких значениях х функция принимает положительные значения?
. При каких значениях х функция принимает положительные значения?