Анализ уравнения движения электропривода

Момент, развиваемый электрическим двигателем, идет на преодоление момента сопротивления машины и на изменение запаса кинетической энергии системы двигатель-рабочая маши­на. Это изменение носит название динамического момента. По значению он равен разности моментов двигателя и рабочей ма­шины. Как следует из анализа правой части выражений (1.10) и (1.11), динамический момент двигателя складывается из двух составляющих.

Первая составляющая связана с изменением частоты вращения, вторая составляющая

или

- с изменением момента инерции в зависимости от угла поворота , времени t или пути L.

В большинстве рабочих машин значения момента инерции J и массы m постоянны или мало изменяются. Этим изменением можно пренебречь и принять J и m постоянными. Тогда

(1.12)

(1.13)

Знак динамического момента влияет на характер движе­ния электропривода. При анализе этих выражений возможны не­сколько случаев.

Первый случай. Пусть М_Д - М_С > 0. Момент инерции J всегда положителен, поэтому Следовательно, при положитель­ном динамической моменте движение будет ускоренным, двигатель с рабочей машиной будут разгоняться.

Второй случай. Если М_Д - М_С < 0 и J > 0, то . Следова­тельно, движение замедляется, и двигатель с рабочей машиной будет тормозиться.

Третий случай. М_Д - М_С = 0, то есть М_Д = М_Стогда

(движение с установившейся частотой вращения).

Приведение моментов и усилий сопротивления к одной

Частоте вращения

Рабочие машины очень часто приводятся в движение электри­ческими двигателями через редукторы или клиноременные передачи. Кинематическая схема подобных передач представлена на рис.1.1, откуда видно, что части механизма вращаются с различными частотами вращения. Из курса теоретической механики извест­но, что на каждой оси (рабочей машины, редуктора, электро­двигателя) действуют свои моменты, значения которых зависят от угловой частоты вращения. Характер изменения моментов и скорости определяется из системы дифференциальных уравнений, составленной для каждой скорости (оси). При одноступенчатом редукторе система состоит из двух уравнений, при двухступен­чатом - из трех и т.д.

Рис.1.1. Кинематическая схема электропривода лебедки.

Решение подобных систем дифференциальных уравнений связа­но с определенными трудностями. Задача упрощается, если вы­полнить приведение (или перерасчет) моментов и усилий к од­ной частоте вращения, одному валу: двигателя или рабочей машины.

В расчетах переходных процессов и установившихся режимов электрического двигателя нас интересуют моменты на его валу, поэтому моменты и усилия приводятся к частоте вращения этого двигателя [7].

Условием приведения является равенство мощностей на валу двигателя реальной и условной, или приведенной кинематических схем.

В реальной схеме мощность на валу рабочей машины

(1.14)

на валу двигателя

(1.15)

Мощность на валу двигателя в приведенной схеме

Р = М_ДВω_Д = М_Сω_Д. (1.16)

Согласно условию приведения моментов левые части двух по­следних уравнений равны, следовательно, равны и правые:

отсюда

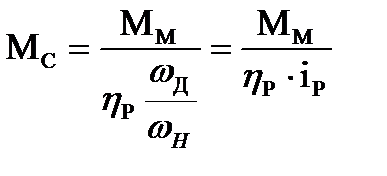, (1.17)

где - передаточное отношение редуктора,

Для поступательного движения получено аналогично:

M_C = F_MV_M/ (1.18); F_C = F_MV_M/ (1.19)

Выражения (1.17...1.19) получены для двигательного режима работы, когда электрическая энергия преобразуется в механи­ческую и передается рабочей машине. В тормозном режиме эле­ктродвигателя направление движения энергии меняется. Меха­ническая энергия от рабочей машины передается к электродви­гателю, который

преобразует ее в электрическую.

Мощность на валу электродвигателя

P_C = = M_M . (1.20)

В этом случае выражения (1.17...1.19) будут иметь вид:

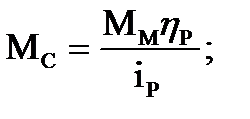(1.21) (1.22) (1.23)

Если редуктор состоит из n ступеней, то передаточное

от­ношение и КПД его:

и

Как отмечалось, в сельскохозяйственном производстве в основном работают тихоходные рабочие машины, для которых необходимы понижающие редукторы. Поэтому по значению приведенные моменты будут меньше реальных. Но, например, у молочных сепараторов установлен повышающий редуктор с , поэтому его приведенный момент сопротивления окажется больше момента барабана сепаратора.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: