Расчётное выражение механической характеристики

Асинхронного двигателя

Уравнение механической характеристики асинхронного двигателя (4.10) затруднительно использовать для практических рас­четов, так как обычно неизвестны величины сопротивлений r₁, r`₂ и х_к. Необходимо получить выражение, в котором использовались бы паспортные данные двигателя. для этого поделим соответственно левую и правую части формулы (5.6) на (5.8):

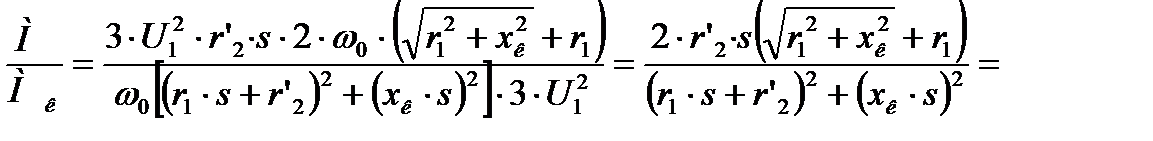
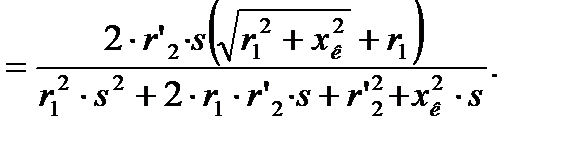
разделим числитель и знаменатель на

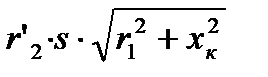
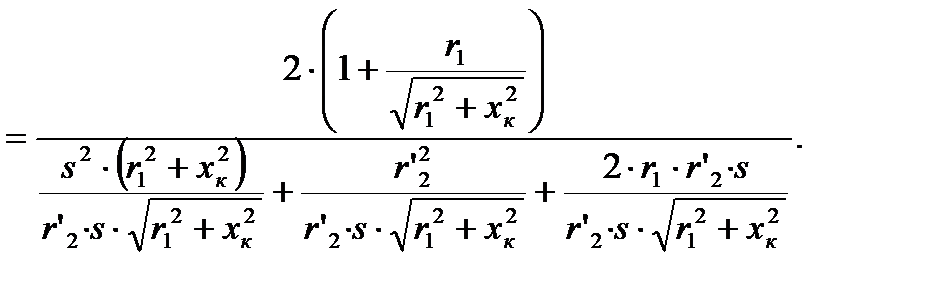
введём обозначение

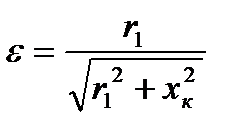
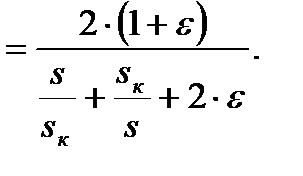
откуда

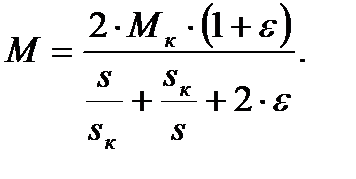(4.18)

Полученное выражение представляет собой уточненное урав­нение механической характеристики асинхронного двигателя. Как уже говорилось, для мощных асинхронных двигателей можно пренебречь величиной r₁ тогда ε = 0. Упрощенное уравнение ме­ханической характеристики:

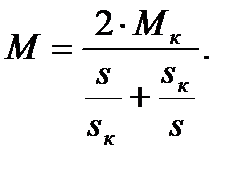(4.19)

Из курса «Электрические машины» известно, что r₁ 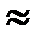r`₂. Следовательно, можно принять ε 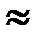s_к. Тогда уравнение механической характеристики будет иметь вид:

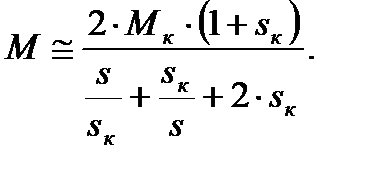(4.20)

Таким образом, для расчета механической характеристики требуются значения только М_к и s_к которые приводятся в пас­порте двигателя. Задаваясь s в требуемых пределах, можно по­лучить график механической характеристики. Выражением (4.20) достаточно точно описывается механическая характеристика асинхронного двигателя с фазным ротором. В двигателях же с короткозамкнутым ротором имеет место вытеснение тока в стержнях ротора. Поэтому механическая характеристика, пост­роенная по этим выражениям, несколько отличается от действи­тельной, особенно на пусковой части, а рабочая часть - сов­падает. Выражение (5.10) обычно используют для качественного анализа механической характеристики.

Для определения s_к в выражении (4.20) принимают s = s_н, М = М_н отношение 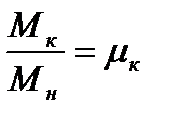- кратность критического момента:

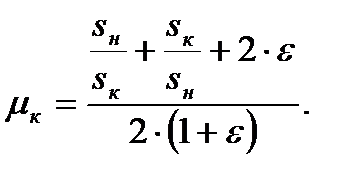
Примем ε = s_к. Тогда это выражение можно записать так:

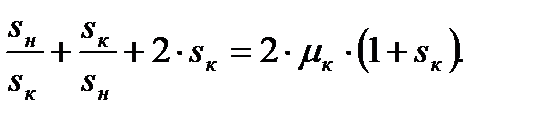(4.21)

Решим его относительно s_к:

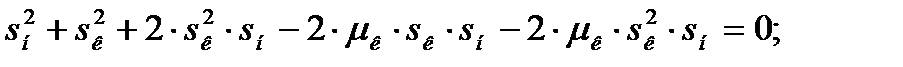
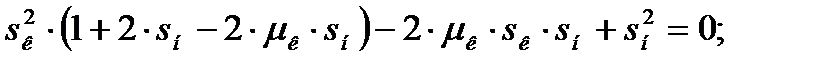
(4.22)

Получим неприведенное полное квадратное уравнение. Решим его относительно s_к:

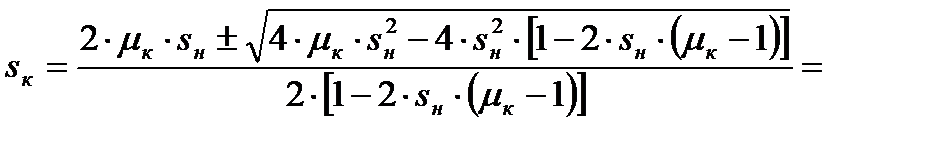
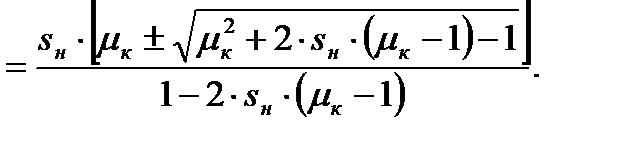(4.23)

 

Значение при знаке «минус» перед корнем не имеет

физического смысла. Таким образом:

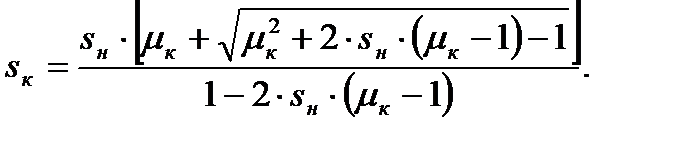(4.24)

При r₁ 0 получим упрощённое выражение:

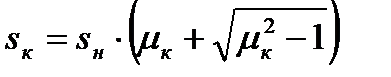. (4.25)

Необходимо отметить, что выражение (4.24) справедливо для двигателей мощностью более 20 кВт. Для двигателей меньшей мощности при расчетах возникают существенные погрешности.

Для анализа механической характеристики асинхронного двигателя рассмотрим упрощенное выражение механической характеристики асинхронного двигателя (4.26):

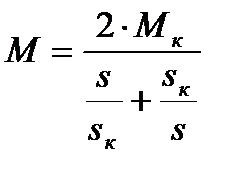. (4.26)

При изменении скольжения двигателя от 0 до (1.2…1.5)s и на рабочей ветви характеристики отношение 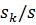больше в 8…10 раз. Поэтому пренебрегаем слагаемым в знаменателе этой формулы. Выражение механической характеристики запишем в виде:

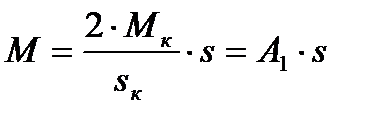. (4.27)

где 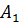- постоянный коэффициент, . Это есть уравне­ние прямой линии. Значит, рабочая часть механической харак­теристики в рассматриваемых пределах линейна. Ближе к крити­ческомy моменту (после М > 0,7... 0,75 ) характеристика ста­новится нелинейной.

При к отношение s/ /s, поэтому пренебрегаем вторым слагаемым в знаменателе, а уравнение механической характери­стики примет вид:

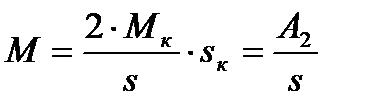. (4.28)

Это выражение - уравнение гиперболы, значит, пусковая ветвь механической характеристики нелинейная.

Построение естественных механической и

Электромеханической характеристик асинхронного двигателя

По каталожным данным

Характеристика асинхронного двигателя естественна при

U_дв = U_н, отсутствии добавочного сопротивления в цепи ротора и статора и при частоте источника питания, равной номинальной

частоте двигателя.

Естественную механическую характеристику по каталожным данным строят при расчетах переходных процессов электропри­водa, определении: частоты вращения регулируемого двигателя, т.е. в тех случаях, когда нужно точно знать частоту вращения и момент [18].

Исходные данные берут из таблички на щитке двигателя или из каталога (5): номинальная мощность двигателя Р_н, кВт; номинальная частота вращения n_н. 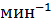, или значение номинального скольжения s_н (обычно в процентах); кратность критического момента М_к/М_н, для двигателей серии 4А ее обозначают μ_к; кратность пускового момента М_п/М_н обозначают μ_п; кратность минимального момента М_min/М_н - μ_min; критическое скольжение –

Естественную механическую характеристику АД строят по пяти точкам с соответствующими координатами:

Первая точка - синхронная угловая скорость ω_о = 2πf/р или ω_о = πn_о/30 , где f - частота питающей сети; n_о = 60f/р; p – число пар полюсов (определяется из типоразмера электродвигателя). В каталожных данных при f = 50 Гц синхронная частота вращения двигателя = 3000, 1500, 1000, 750, 600, 500 и т.д. 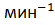. Момент двигателя при ω_о равен нулю, т.е. эта точка лежит на оси ординат – частоты вращения;

Вторая точка – номинальные: частота вращения ω_н = πn_н/30 или 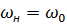(1- s_н), и момент М_н = Р_н • 10^-3/ ω_н, Н•м.

Третья точка – критические: момент и угловая скорость ω_к = ω_о(1 - s_к).

Если значение критического скольжения не приводится в справочной литературе, его определяют по формуле:

 

 

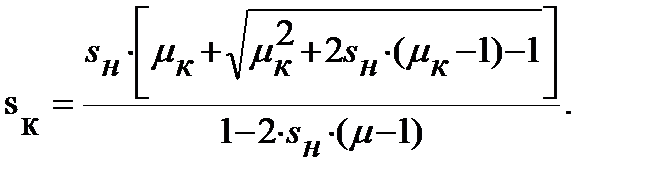
Четвертая точка – минимальные: момент М_м = М_н скорость

ω_м = ω_о(1 - s_м), s_m= 6/7 для всех двигателей:

Пятая точка - пусковой момент М_п = М_н , ω_о = 0.

Для более точного построения механической характеристики в области критического скольжения необходимо взять несколько промежуточных точек и определить значения момента по (4.20).

Рис. 4.3. Построение естественной механической характеристики

асинхронного двигателя.

Соединив плавной линией рассчитанные точки, получим график механической характеристики асинхронного двигателя (рис.4.3). На этой же рисунке пунктиром приведен график ме­ханической характеристики, построенной по уравнению (4.19).

Естественная электромеханическая характеристика асинхрон­ного двигателя I = f(ω) нужна при построении нагрузочных диаг­рамм для проверки двигателя на нагрев.

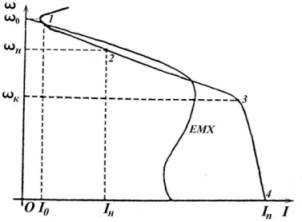
Рис.4.4. Построение естественной электромеханической

характеристики асинхронного двигателя.

Исходные данные можно взять из таблички двигателя и каталога: номинальная мощность двигателя Р_н, кВт; номинальное линейное напряжение двигателя U_н, B; номинальные коэффициенты: полезного действия η_н и мощности cosφ; кратность пускового тока 1_п; номинальное и критическое скольжение s_н, s_к. Естественную электромеханическую характеристику строят по четырем характерным точкам:

Первая точка имеет координаты:синхронная угловая скорость

ω_о = 2πf/р или ω_о = πn_о/30 и ток статора, соответствующий ω_о (ток намагничивания):

I_c = I _н(sinφ_н - cosφ_н/2 _к), (4.30)

где _к - кратность критического момента;

Вторая точка соответствует номинальным значениям:

I_н = P_н • 10³/( • U_н • η_н • cosφ_н); ω_{н =} ω_о(1 - s_н);

Третья точка соответствует критическому скольжению дви­гателя:

ω_{к =} ω_о(1 - s_к); I_к = (0,7…0,8)I_пуск

Четвертая точка - пусковая: I_пуск = I_н • i_п; ω = 0

Соединив полученные точки плавной линией, получим график электромеханической характеристики. Обычно ее строят на одном графике с механической (рис.4.4).

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: