 |
Причиной и движущей силой переноса экстенсивных величин является разница в значении интенсивных свойств (или потенциалов переноса).
|
|
|
|
Причиной и движущей силой переноса экстенсивных величин является разница в значении интенсивных свойств (или потенциалов переноса).
В разных точках рабочего объема технологического аппарата в общем случае значения интенсивных величин (потенциалов переноса) различны. Поверхности в объеме тела с одинаковым значением потенциала переноса называются изоповерхностями. Перенос субстанции вдоль изоповерхности не происходит, а только лишь от одной изоповерхности к другой, от изоповерхности с большим значением потенциал к изоповерхности с меньшим значением потенциала.
 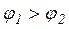
| Изменение потенциала на единицу длины по нормали называется градиентом.
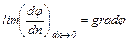 dn→ 0
Интенсивность переноса прямопропорцианальна gradφ
dn→ 0
Интенсивность переноса прямопропорцианальна gradφ
|
В соответствии с правилами математики градиент направлен в сторону повышения потенциала, в то время как субстанция переносится от большего потенциала к меньшему. Поэтому в соотношениях, связывающих удельные потоки субстанции и градиенты, перед последними ставится знак «минус».
Виды переноса
Удобнее всего механизмы переноса классифицировать по масштабу, в котором осуществляется элементарный акт переноса.
Наинизший уровень – квантовый: элементарный акт переноса заключается в излучении и поглощении элементарной частицы – кванта. Механизм переноса на квантовом уровне называется излучением.
Второй более высокий уровень связан с тепловым движением молекул.
|
Молекулярный перенос | ||
| Импульс Механизм переноса импульса на молекулярном уровне – вязкостное трение или вязкость. Перенос импульса подчиняется закону Ньютона. | Тепло Механизм переноса тепла на молекулярном уровне – теплопроводность. Перенос тепла описывается уравнением Фурье: | Вещество Механизм переноса вещества на молекулярном уровне – диффузия. Описывается уравнением Фика: |
Закон Ньютона
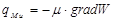 μ – коэффициент динамической вязкости;
μ – коэффициент динамической вязкости;
 = ν – коэффициент кинематическая вязкость = ν – коэффициент кинематическая вязкость
 W – скорость перемещения;
W – скорость перемещения;
| Закон Фурье

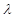 – коэффициент теплопроводности;
cp – удельная теплоемкость
при P = const; – коэффициент теплопроводности;
cp – удельная теплоемкость
при P = const;
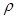 – плотность; – плотность;
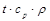 = i – объемная энтальпия; = i – объемная энтальпия;
 = a –коэффициент температуропроводности, характеризует скорость нагревания и охлаждения тела. = a –коэффициент температуропроводности, характеризует скорость нагревания и охлаждения тела.
| Закон Фика
 c – концентрация переносимого вещества;
D – коэффициент молекулярной диффузии.
c – концентрация переносимого вещества;
D – коэффициент молекулярной диффузии.
|
Таким образом, молекулярный перенос массы qМc, энергии qМt, импульса qМи описываются идентичными по форме уравнениями, которые могут быть объединены следующим выражением:
|
|
|
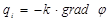 - общее уравнение
- общее уравнение
где k – коэффициент пропорциональности, в зависимости от вида переноса принимающий значения D, a, 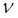 (м2/с) (для газов D
(м2/с) (для газов D  a
a 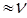 );
);
φ – потенциал переноса.
Высший уровень переноса связан с движением потоков. Перемещающиеся массы жидкости несут с собой и количество движения, и тепло, и вещество, и таким образом переносят их. Этот механизм называется конвекцией или конвективным переносом.
Плотность конвективного потока qк массы, энергии и импульса на каждом участке поверхности можно выразить следующим образом:
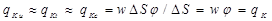
где Δ S – участок поверхности, расположенный нормально вектору скорости.
Таким образом, в случае молекулярного и конвективного переноса массы или энергии плотность потока q складывается из двух составляющих: q = qм + qк, (применимо при переносе тепла в жидкости). При переносе тепла через стенку: q = qм
Основное уравнение переноса субстанции
В рассматриваемом объеме жидкости в общем случае существуют источники субстанций, характеризующиеся объемной удельной плотностью потока  (Дж/м2с; кг/м2с).
(Дж/м2с; кг/м2с).
|
|
|
Выделим на поверхности этого объема, элемент поверхности dS и представим его в векторной форме, умножим на единичный вектор n, расположенный по нормали к этому элементу и направленный из объема V (ndS = dS). Найдем результирующий поток массы, энергии и импульса, входящий в объем V:
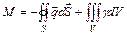
Вместе с тем, это же количество субстанции М можно определить как изменение во времени потенциала φ по всему объему:
 .
.
Приравняв эти выражения и проделав необходимые математические операции, получим:
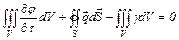 .
.
Согласно теореме Остроградского – Гаусса, интеграл от нормальной составляющей вектора по поверхности равен интегралу от дивергенции вектора по объему:
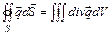 .
.
С учетом этого уравнение (1. 22) приобретает следующий вид:
 ,
,
отсюда следует:

На основе уравнения переноса субстанций можно получить дифференциальные уравнения, описывающие распределение скоростей, концентраций и температур во времени и пространстве, что необходимо для решения многих важных технических задач (только для однофазных изотропных сплошных сред).
|
|
|


