 |
А.И. Маринин. Материалы для подготовки к экзамену. следствия из них. Необходимые и достаточные условия
|
|
|
|
А. И. Маринин
Материалы для подготовки к экзамену
Здесь выставлены материалы для подготовки к экзамену по геометрии в 10 классе. Надеюсь, лицеистам поможет предложенная систематизация теоретических вопросов.
Ссылки:
( А ) – Атанасян. Геометрия. 10-11 классы.
( К ) – Киселев. Геометрия. 10-11 классы.
Предмет и логическое строение стереометрии. Аксиомы стереометрии и
следствия из них
Предметом стереометрии является изучение геометрических свойств фигур, не все точки которых лежат в одной плоскости. Такие фигуры называются пространственными. Представление о них вы имеете из опыта. В их числе: точки, прямые, плоскости (учение о взаимном расположении точек и прямых на плоскости есть планиметрия), а также различные поверхности и ограниченные ими тела, о которых будет сказано в должном месте.
Геометрическими являются такие свойства фигур, которые могут быть выражены в терминах основных понятий геометрии. Примеры основных понятий: точка, прямая, плоскость, принадлежность точки прямой, расстояние между точками, наложение фигур, число, множество и т. д. Список будет уточняться и пополняться с продвижением вглубь курса.
В стереометрии (как и ранее в планиметрии) содержательными геометрическими суждениями являются аксиомы и теоремы. Истинность аксиом в геометрической теории объявляется априорно, т. е. аксиомы не выводимы из других суждений. Истинность теорем определяется путем логического вывода из суждений, истинность которых уже установлена (в том числе из аксиом). Умозаключение, устанавливающее истинность теоремы, называется ее доказательством.
Некоторые аксиомы стереометрии:
|
|
|
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
А2. Если две точки прямой лежат в некоторой плоскости, то все точки прямой лежат в этой плоскости.
Говорят, что прямая лежит в плоскости, плоскость проходит через прямую.
Следствие: прямая, не лежащая в плоскости, имеет с этой плоскостью не более одной общей точки.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую. Т. о., пересечение двух пересекающихся плоскостей содержит целую прямую.
А4. Существуют четыре точки, не лежащие в одной плоскости.
Все аксиомы и теоремы планиметрии сохраняются и в стереометрии. Они истинны в любой плоскости пространства.
По традиции точки обозначаются прописными латинскими, прямые - строчными латинскими или двумя прописными латинскими, плоскости - строчными греческими буквами или тремя прописными латинскими буквами, именующими три точки, не лежащие на одной прямой (согласно аксиоме А1, такие три точки однозначно определяют плоскость).
Следствия из аксиом:
Теорема 1. Через прямую l и точку вне ее проходит плоскость, притом только одна.
Доказательство. Существование: две различные точки прямой и данная точка образуют конфигурацию точек, удовлетворяющую аксиоме А1. В плоскости 
, задаваемой этой конфигурацией, содержатся все точки прямой l (аксиома А2). Единственность плоскости гарантируется аксиомой А1.
Теорема 2. Через две пересекающиеся прямые проходит плоскость, притом только одна.
Доказательство. Существование: взяв на каждой из прямых по одной точке, отличной от точки пересечения A, проведем плоскость через выбранные точки и точку A, что можно сделать по аксиоме А1. Полученная плоскость, согласно аксиоме А2, содержит каждую из данных прямых. Единственность следует из аксиомы А1.
Теорема 3. Через две параллельные прямые проходит единственная плоскость.
|
|
|
(Две параллельные прямые содержатся в единственной плоскости).
Доказательство. То, что данные параллельные прямые лежат в одной плоскости, непосредственно следует из определения параллельности прямых. Единственность обеспечивается аксиомой А1 (достаточно выбрать две различные точки на одной из прямых и одну точку на другой прямой) или следует из теоремы 1.
Необходимые и достаточные условия
Любая теорема есть суждение, утверждающее, что если истинно положение A, то является истинным другое положение B. Пример: диагонали ромба взаимно перпендикулярны (если данный четырехугольник есть ромб, то его диагонали взаимно перпендикулярны). Таким образом, теорема имеет вид: " Если A, то B". В такой формулировке положение A называется условием, а B - заключением теоремы.
Предположим, что доказана некоторая теорема " если A, то B", т. е. установлена истинность этого суждения. Говорят, что положение B есть следствие положения A, или же говорят, что положение B является необходимым признаком положения A, а положение A является достаточным признаком положения B, и пишут A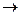 
B. В рассмотренной ситуации B может оставаться истинным и при ложности A.
Теорема " если B, то A" является обратной к теореме " если A, то B". Она требует отдельного доказательства. Если обратная теорема истинна, т. е. верно как A 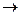B, так и B 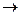A, то B является необходимым признаком A (так как A 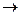B), вместе с тем B является и достаточным признаком A (так как B 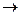A). В этом случае говорят, что положение B является необходимым и достаточным признаком положения A. Точно так же положение A является необходимым и достаточным признаком положения B.
В тех случаях, когда истинны обе теоремы - прямая и обратная, - их можно формулировать в виде одного утверждения: " Для того, чтобы имело место A, необходимо и достаточно, чтобы имело место B" или " A имеет место тогда и только тогда, когда имеет место B". Доказательство теоремы, в которой утверждается необходимость и достаточность некоторого условия, состоит из двух частей, так как такая теорема представляет собой соединение двух взаимно обратных теорем. В одной из частей доказывается необходимость, в другой достаточность условия.
|
|
|
Пример. Теорема. Для того, чтобы треугольник ABC был прямоугольным с прямым углом C, необходимо и достаточно выполнение условия c2 = a2 + b2.
Схема доказательства:
Необходимость. Если треугольник ABC прямоугольный с прямым углом C, то c2 = a2 + b2.
Достаточность. Если в треугольнике ABC c2 = a2 + b2, то он прямоугольный, причем угол C - прямой.
Замечание. В стереометрии, как и в планиметрии, возможны задачи на построение. В задачах на построение в стереометрии будем предполагать, что мы имеем возможность:
проводить плоскость через три заданные точки (через точку и прямую, через две пересекающиеся прямые, через две параллельные прямые);
получать прямую пересечением двух плоскостей; проводить прямую через две точки пространства (в какой-нибудь плоскости, содержащей эти точки);
в любой плоскости пространства производить все построения циркулем и линейкой, которые изучаются в планиметрии.
Задача. Построить прямую, проходящую через данную точку A пространства и пересекающую две данные прямые пространства.
|
|
|
