 |
Свойства параллелепипеда. Перпендикулярные прямые в пространстве
|
|
|
|
Свойства параллелепипеда
Теорема 16 (свойства параллелепипеда).
1. Противоположные грани параллелепипеда равны и параллельны.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся в этой точке пополам.
Доказательство дано в А(стр. 26-27). Оно правильное.
Секущая плоскость ( плоскость сечения ) многогранника - любая плоскость пространства, пересекающая данный многогранник. Так как секущая плоскость пересекает грани многогранника по отрезкам (они и несущие их прямые называются следами секущей плоскости на гранях), фигура, составленная из таких отрезков (следов) является многоугольником, и этот многоугольник называется сечением данного многогранника данной плоскостью. Такой способ построения сечений, при котором разыскиваются следы секущей плоскости на гранях многогранника, называется методом следов.
При решении задач на сечения основную роль играют следующие известные из теории факты (см. аксиомы и теоремы стереометрии):
1) если две плоскости имеют две общие точки, то они пересекаются по прямой, проходящей через эти точки;
2) если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны;
3) если плоскость содержит прямую, параллельную другой плоскости, и пересекает ту плоскость, то прямая пересечения плоскостей параллельна данной прямой;
4) через прямую, параллельную данной плоскости, можно провести плоскость, параллельную данной, притом только одну;
5) отрезки прямых, заключенные между двумя параллельными плоскостями, равны.
Иногда для построения следа секущей плоскости на грани многогранника может потребоваться отыскание двух точек, принадлежащих плоскости грани (не обязательно на ребрах или внутри грани). Таким образом, построение сечения сводится к нахождению в плоскостях граней по две точки, принадлежащие секущей плоскости.
|
|
|
Задача. Даны две скрещивающиеся прямые l и m и точка O, не принадлежащая ни одной из них. Всегда ли существует прямая, проходящая через точку O и пересекающая обе данные прямые? Может ли таких прямых быть две?
Перпендикулярные прямые в пространстве
Определение. Две прямые l и m в пространстве называются перпендикулярными, если угол между ними равен 
.
Обозначение: l 
m.
Теорема 17. Если прямые l и m параллельны и l перпендикулярна к третьей прямой k, то прямые m и k перпендикулярны.
Доказательство. Проведем через любую точку A пространства, не принадлежащую ни одной из прямых l и k прямые AL и AK, параллельные соответственно прямым l и k (это можно сделать по теореме 4); так как по условию l k, 
LAK= . По теореме 6, прямая m параллельна AL (m || l || AL), следовательно, угол между прямыми m и k равен углу между прямыми AL и AK (по определению угла между прямыми), то есть равен . Теорема доказана.
Определение. Прямая l называется перпендикулярной к плоскости 
, если она перпендикулярна к любой прямой, лежащей в плоскости .
Лемма. Если прямая перпендикулярна к плоскости, то она пересекает эту плоскость.
Доказательство - от противного.
Теорема 18. Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Доказательство. Пусть l||m, 
, k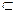 
- произвольная прямая плоскости . l k, следовательно, m k (теорема 17). В силу произвольности прямой k, m .
Теорема 19. Если две прямые перпендикулярны к одной и той же плоскости, то они параллельны.
Доказательство. Пусть l и m . Пусть 
, где m1||l. По теореме 18 m1 . Если m 
m1, то (теорема 2) существует плоскость 
, содержащая прямые m и m1. Прямая m1 пересекает плоскость , поэтому плоскости и пересекаются по некоторой прямой k, при этом m k и m1 k. Но через точку A в плоскости проходит только одна прямая, перпендикулярная прямой k, поэтому m1=m и l||m, что и требовалось.
|
|
|
Теорема 20 (признак перпендикулярности прямой и плоскости).
Если прямая l перпендикулярна к двум пересекающимся прямым m и k, лежащим в плоскости , то прямая l перпендикулярна плоскости .
Доказательство. См. К(стр. 13-14)
|
|
|
