 |
Теорема о трех перпендикулярах
|
|
|
|
Теорема о трех перпендикулярах
Теорема 26. Дана плоскость  , точка A
, точка A  , перпендикуляр AB и наклонная AH к
, перпендикуляр AB и наклонная AH к  из точки A, n - некоторая прямая плоскости
из точки A, n - некоторая прямая плоскости  . Если проекция BH наклонной AB перпендикулярна к n, то наклонная AB также перпендикулярна к n.
. Если проекция BH наклонной AB перпендикулярна к n, то наклонная AB также перпендикулярна к n.
Доказательство.  (признак перпендикулярности прямой и плоскости)
(признак перпендикулярности прямой и плоскости)  , ч. т. д.
, ч. т. д.
Теорема 26’ (обратная). Дана плоскость  , точка A
, точка A  , перпендикуляр AB и наклонная AH к
, перпендикуляр AB и наклонная AH к  из точки A, n - некоторая прямая плоскости
из точки A, n - некоторая прямая плоскости  . Если наклонная AB перпендикулярна к n, то проекция BH наклонной AB также перпендикулярна к n.
. Если наклонная AB перпендикулярна к n, то проекция BH наклонной AB также перпендикулярна к n.
Доказательство.  (признак перпендикулярности прямой и плоскости)
(признак перпендикулярности прямой и плоскости)  , ч. т. д.
, ч. т. д.
Двугранный угол
Любая прямая плоскости разделяет эту плоскость на две полуплоскости; эта конструкция означает следующее: отрезок, проходящий через две точки, лежащие в одной полуплоскости относительно разделяющей прямой, не пересекает эту прямую; напротив, отрезок, соединяющий две точки, принадлежащие разным полуплоскостям, пересекает прямую, которая называется общей границей этих полуплоскостей.
Определение. Фигура, образованная двумя различными полуплоскостями  и
и  с общей границей l=AB, называется двугранным углом с ребром l=AB и гранями (сторонами)
с общей границей l=AB, называется двугранным углом с ребром l=AB и гранями (сторонами)  и
и  .
.
Проведем из произвольной точки A 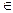 l=AB перпендикуляры AP
l=AB перпендикуляры AP  l и AQ
l и AQ  l, где P
l, где P 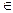
 , Q
, Q 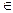
 . Угол PAQ называется линейным углом двугранного угла PABQ.
. Угол PAQ называется линейным углом двугранного угла PABQ.
Лемма. Все линейные углы данного двугранного угла равны между собой.
Доказательство. Два линейных угла равны как углы с сонаправленными сторонами.
Двугранный угол измеряется каким-нибудь его линейным углом.
Говорят, что угол между двумя параллельными плоскостями равен 0.
Замечание. Так как ребро двугранного угла перпендикулярно сторонам линейного угла, соответственно лежащим в гранях двугранного угла, это ребро перпендикулярно плоскости, содержащей стороны линейного угла.
|
|
|
Определение. Две плоскости называются перпендикулярными, если угол между ними прямой.
Теорема 27 ( признак перпендикулярности двух плоскостей). Если l 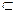
 и l
и l 
 , то
, то 

 (если плоскость
(если плоскость  проходит через прямую l, перпендикулярную другой плоскости
проходит через прямую l, перпендикулярную другой плоскости  , то плоскости
, то плоскости  и
и  перпендикулярны).
перпендикулярны).
Доказательство. Пусть l 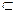
 и l
и l 
 ; так как l
; так как l 
 ,
,  если l=AB, то
если l=AB, то  проведем в
проведем в  через точку B прямую BD
через точку B прямую BD  BC; получим угол ABD - линейный угол двугранного угла рлоскостей
BC; получим угол ABD - линейный угол двугранного угла рлоскостей  и
и  . Поскольку AB
. Поскольку AB 
 , угол ABD - прямой.
, угол ABD - прямой.
Непосредственное
Следствие. Плоскость 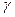 , перпендикулярная прямой l пересечения двух плоскостей
, перпендикулярная прямой l пересечения двух плоскостей  и
и  , перпендикулярна к каждой из плоскостей
, перпендикулярна к каждой из плоскостей  и
и  .
.
Прямоугольный параллелепипед
Определение. Параллелепипед, в основаниях которого лежат прямоугольники, а боковые ребра перпендикулярны основаниям, называется прямоугольным. Двугранные углы при ребрах параллелепипеда называются его двугранными углами.
Теорема 28.
1. В прямоугольном параллелепипеде все грани - прямоугольники.
2. Все двугранные углы прямоугольного параллелепипеда прямые.
Доказательство. Очевидно (но провести нужно).
Определение. Длины ребер прямоугольного параллелепипеда, исходящих из одной его вершины, называются измерениями параллелепипеда.
Теорема 29. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Доказательство. Теорема Пифагора.
Следствие. Диагонали прямоугольного параллелепипеда равны.
Определение. Кубом называется прямоугольный параллелепипед, все измерения которого равны.
Все грани куба - равные квадраты.
Теорема 30. Площадь ортогональной проекции многоугольника на некоторую плоскость  равна произведению площади многоугольника на косинус двугранного угла между плоскостью многоугольника и плоскостью
равна произведению площади многоугольника на косинус двугранного угла между плоскостью многоугольника и плоскостью  .
.
|
|
|
Доказательство. Прямое вычисление: для треугольника h=Hcos  , где
, где  - линейный угол нужного двугранного угла; произвольный (выпуклый) многоугольник разбивается диагоналями на треугольники, причем площадь многоугольника равна сумме площадей треугольников разбиения (аддитивность площади).
- линейный угол нужного двугранного угла; произвольный (выпуклый) многоугольник разбивается диагоналями на треугольники, причем площадь многоугольника равна сумме площадей треугольников разбиения (аддитивность площади).
|
|
|


