 |
Параллельные прямые в пространстве
|
|
|
|
Параллельные прямые в пространстве
Определение параллельных прямых было дано в курсе планиметрии, именно: две прямые, лежащие в одной плоскости и не имеющие общих точек, называются параллельными. a||b - обозначение параллельности прямых a и b. Так, две параллельные прямые пространства всегда лежат в одной плоскости.
Теорема 4. Через любую точку A пространства, не лежащую на прямой l, проходит прямая m, параллельная l, притом только одна.
Доказательство. Рассмотрим плоскость  , проходящую через точку A и прямую l. В плоскости
, проходящую через точку A и прямую l. В плоскости  через точку A проходит (и единственная) прямая m, параллельная l (факт, известный из планиметрии). С другой стороны, любая прямая, проходящая через A параллельно l, должна лежать в одной плоскости с l и с точкой A, но A и l определяют плоскость однозначно, и это есть плоскость
через точку A проходит (и единственная) прямая m, параллельная l (факт, известный из планиметрии). С другой стороны, любая прямая, проходящая через A параллельно l, должна лежать в одной плоскости с l и с точкой A, но A и l определяют плоскость однозначно, и это есть плоскость  .
.
В доказательстве были использованы следствия из аксиом стереометрии (теоремы 1 и 3).
Замечание. Будем говорить, что промежутки на прямой (интервалы, отрезки и т. д. ) параллельны между собой, если несущие их прямые параллельны.
Параллельность трех прямых. Скрещивающиеся прямые
Теорема 5. Если одна из двух параллельных прямых пересекает некоторую плоскость, то другая прямая также пересекает эту плоскость.
Доказательство. Пусть  - данная плоскость, l||m,
- данная плоскость, l||m,  - плоскость, содержащая l и m, A=l
- плоскость, содержащая l и m, A=l 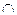
 . Так как A
. Так как A 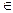 l
l 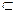
 и A
и A 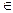
 , плоскости
, плоскости  и
и  имеют, по аксиоме A3, общую прямую n (проходящую через точку A). n пересекает l, поэтому n пересекает прямую m||l в плоскости
имеют, по аксиоме A3, общую прямую n (проходящую через точку A). n пересекает l, поэтому n пересекает прямую m||l в плоскости  в некоторой точке B, которая, как точка прямой n, лежит в плоскости
в некоторой точке B, которая, как точка прямой n, лежит в плоскости  . Остается установить, что прямая m именно пересекает плоскость
. Остается установить, что прямая m именно пересекает плоскость  , а не лежит в ней. Если m лежит в
, а не лежит в ней. Если m лежит в  , то m является прямой пересечения плоскостей
, то m является прямой пересечения плоскостей  и
и  , следовательно, совпадает с n; но n пересекает прямую l, а не параллельна ей.
, следовательно, совпадает с n; но n пересекает прямую l, а не параллельна ей.
|
|
|
Теорема 6. Если каждая из двух прямых l и m параллельна одной и той же прямой n, то прямые l и m параллельны.
Доказательство. Пусть l||n, m||n, A 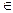 m и
m и  - плоскость, проходящая через l и A (теорема 1). Прямая m уже имеет с плоскостью
- плоскость, проходящая через l и A (теорема 1). Прямая m уже имеет с плоскостью  общую точку A. Если m пересекает
общую точку A. Если m пересекает  , то (теорема 5) n также пересекает
, то (теорема 5) n также пересекает  , значит, по той же теореме 5, l пересекает
, значит, по той же теореме 5, l пересекает  (а не содержится в
(а не содержится в  ); отсюда следует, что прямая m содержится в плоскости
); отсюда следует, что прямая m содержится в плоскости  . Предположив, что l и m пересекаются в точке B, придем к тому, что через точку B проходят две различные прямые l и m, параллельные одной и той же прямой n, что противоречит теореме 4. Имеем: прямые l и m лежат в одной плоскости и не имеют общих точек. Это означает l||m, ч. т. д.
. Предположив, что l и m пересекаются в точке B, придем к тому, что через точку B проходят две различные прямые l и m, параллельные одной и той же прямой n, что противоречит теореме 4. Имеем: прямые l и m лежат в одной плоскости и не имеют общих точек. Это означает l||m, ч. т. д.
Определение. Прямые l и m, не лежащие в одной плоскости, называются скрещивающимися.
Признаком (именно с его помощью устанавливается скрещиваемость прямых в задачах) скрещивающихся прямых является
Теорема 7. Если прямая AB лежит в плоскости  , а прямая CD пересекает эту плоскость в точке C, не лежащей на прямой AB, то прямые AB и CD скрещиваются.
, а прямая CD пересекает эту плоскость в точке C, не лежащей на прямой AB, то прямые AB и CD скрещиваются.
Доказательство. По условию, AB 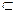
 , CD
, CD 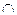
 =C, CD
=C, CD 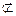
 , C
, C 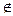 AB. Предположим, что AB
AB. Предположим, что AB 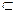
 , CD
, CD 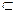
 . Получим AB
. Получим AB 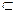
 , C
, C 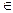
 , C
, C 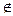 AB, значит
AB, значит  =
=  (теорема 1) и CD
(теорема 1) и CD 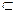
 - противоречие. Таким образом, прямые AB и CD не могут лежать в одной плоскости, то есть являются скрещивающимися.
- противоречие. Таким образом, прямые AB и CD не могут лежать в одной плоскости, то есть являются скрещивающимися.
Параллельность прямой и плоскости
Если прямая имеет общие точки с некоторой плоскостью  , то эта прямая целиком принадлежит плоскости
, то эта прямая целиком принадлежит плоскости  (в случае, когда общих точек не менее двух) или пересекает плоскость
(в случае, когда общих точек не менее двух) или пересекает плоскость  в единственной точке; если же общих точек прямая и плоскость не имеют, они называются параллельными.
в единственной точке; если же общих точек прямая и плоскость не имеют, они называются параллельными.
Определение. Прямая l и плоскость  называются параллельными, если они не
называются параллельными, если они не
имеют общих точек.
Обозначение: l||  .
.
Теорема 8 (признак параллельности прямой и плоскости). Если прямая l параллельна некоторой прямой m, лежащей в плоскости  , то l||
, то l||  .
.
|
|
|
Доказательство. Проведем через l и m плоскость  (теорема 3); если P
(теорема 3); если P 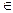 l
l 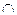
 , то (так как l
, то (так как l 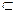
 ) P
) P 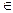
 и P
и P 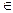

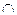
 ; но
; но 
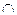
 =m, значит P
=m, значит P 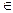 m. Получили P
m. Получили P 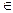 l
l  m - противоречие с параллельностью l и m.
m - противоречие с параллельностью l и m.
Теорема 9. Если плоскость  содержит прямую l, параллельную другой плоскости
содержит прямую l, параллельную другой плоскости  , и пересекает эту плоскость, то прямая m пересечения плоскостей
, и пересекает эту плоскость, то прямая m пересечения плоскостей  и
и  параллельна прямой l.
параллельна прямой l.
Доказательство. l, m 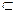
 , то есть прямые l и m не могут быть скрещивающимися. Если A
, то есть прямые l и m не могут быть скрещивающимися. Если A  l
l  m, то A
m, то A 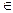 l
l 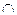
 - противоречие (l||
- противоречие (l||  ).
).
Теорема 10. Если прямые l и m параллельны и l параллельна плоскости  , то m также параллельна плоскости
, то m также параллельна плоскости  или содержится в ней.
или содержится в ней.
Доказательство. l||m, l|| 
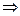 m не пересекает
m не пересекает  (теорема 5), то есть не может иметь с
(теорема 5), то есть не может иметь с  единственной общей точки
единственной общей точки 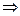 m
m 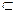
 или m||
или m||  .
.
Скрещивающиеся прямые
Теорема 11. Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, притом только одна.
Доказательство. Пусть прямые l и m скрещиваются. Проведем через l и точку M на прямой m плоскость  и в этой плоскости через точку M прямую n параллельно l. Так как прямая l не параллельна m, прямые l и n не совпадают, следовательно, пересекаясь в точке M, однозначно определяют плоскость
и в этой плоскости через точку M прямую n параллельно l. Так как прямая l не параллельна m, прямые l и n не совпадают, следовательно, пересекаясь в точке M, однозначно определяют плоскость  . Прямая l не лежит в плоскости
. Прямая l не лежит в плоскости  (иначе l и m не были бы скрещивающимися). Прямая n плоскости
(иначе l и m не были бы скрещивающимися). Прямая n плоскости  параллельна прямой l, поэтому
параллельна прямой l, поэтому  ||l (теорема 8). Аналогично, через прямую l проходит плоскость, параллельная m. Единственность: пусть плоскость
||l (теорема 8). Аналогично, через прямую l проходит плоскость, параллельная m. Единственность: пусть плоскость 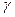 содержит прямую m и параллельна прямой l; через прямую l и точку M (ту самую, в которой пересекаются прямые l и n) проходит плоскость
содержит прямую m и параллельна прямой l; через прямую l и точку M (ту самую, в которой пересекаются прямые l и n) проходит плоскость 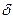 , пересекающая
, пересекающая 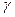 по прямой k||l (теорема 9); но через точку M проходит только одна прямая, параллельная l (теорема 4), поэтому прямая k совпадает с прямой n, а плоскость
по прямой k||l (теорема 9); но через точку M проходит только одна прямая, параллельная l (теорема 4), поэтому прямая k совпадает с прямой n, а плоскость 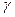 совпадает с построенной плоскостью
совпадает с построенной плоскостью  .
.
Задача. Являются ли прямые скрещивающимися, если: а) обе они не лежат в плоскости  ; б) одна из них лежит в плоскости
; б) одна из них лежит в плоскости  , а другая лежит в плоскости
, а другая лежит в плоскости  ; в) одна из них лежит в плоскости
; в) одна из них лежит в плоскости  , а другая пересекает
, а другая пересекает  ; г) плоскость
; г) плоскость  проходит через две точки одной и две точки другой?
проходит через две точки одной и две точки другой?
|
|
|


