 |
Трехгранный угол. Доказательство можно прочитать, например, в учебнике Киселева.. Понятие многогранника. Призма
|
|
|
|
Трехгранный угол
Определение. Даны плоский многоугольник F и точка S, не принадлежащая плоскости этого многоугольника. Фигура, являющаяся объединением всех лучей с общим началом S и пересекающих F, называется многогранным углом (n-гранным) углом.
S – вершина, лучи SA, SB, SC, … (точки A, B, C, … - вершины многоугольника F ) – ребра, плоскости ASB, BSC, … - грани, углы ASB, BSC, … - плоские углы многогранного угла.
Точка P называется внутренней точкой многогранного угла, если луч SP пересекает внутренность многоугольника F.
Две грани, имеющие общее ребро, образуют двугранный угол многогранного угла.
Если F – выпуклый многоугольник, соостветствующий многогранный угол называется выпуклым.
Обозначение: SABC… (A, B, C, … - точки последовательных ребер, то есть вершины многоугольника, являющегося пересечением многогранного угла плоскостью, пересекающей все ребра угла).
При n=3 получаем трехгранный угол – основной для нас объект изучения. Величины трех плоских и трех двугранных углов – основные параметры трехгранного угла.
Теорема 31. В трехгранном угле каждый плоский угол меньше суммы двух других плоских углов и больше их разности.
Доказательство.
Пусть 
– наибольший из плоских углов трехгранного угла SABC. В плоскости ASC построим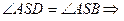 
луч SD лежит внутри угла ASC (или точки D и C совпадают). Возьмем SB=SD и проведем прямую ADC. В треугольнике ABC: AD + DC < AB + BC (даже если DC=0) – это неравенство треугольника. 
. Теперь рассмотрим треугольники CSD и CSB: SD=SB, SC=SC, DC< BC, следовательно, 
, т. е. 
. 
.
Теорема 32. Сумма плоских углов трехгранного угла меньше 
.
Доказательство. Тот же чертеж, что в теореме 31: применим теорему 31 к каждому из трехгранных углов с вершинами S, A, B, C и сложим почленно полученные 12 неравенств; после очевидных преобразований придем к взыскуемому результату.
|
|
|
Теорема 33. Сумма плоских углов выпуклого многогранного угла меньше .
Доказательство можно прочитать, например, в учебнике Киселева.
Теорема 34. Если в трехгранном угле два плоских угла равны, проекцией ребра, являющегося общей стороной равных углов, на плоскость противолежащей грани является биссектриса плоского угла (или ее продолжение) этой грани.
Доказательство. Очевидно.
Теорема 35 (теорема косинусов для трехгранного угла). Пусть 
– плоские углы трехгранного угла, A, B, C - противолежащие им двугранные углы. Тогда 
.
Доказательство. Пусть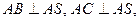 
SA = a. Тогда 
. Выразим BC2 по теореме косинусов из треугольников BSC и BAC и приравняем полученные выражения; после шаблонных преобразований получим что надо.
Теорема 36 (вторая теорема косинусов для трехгранного угла).
.
Доказательство. Опустим из внутренней точки трехгранного угла перпендикуляры на грани трехгранного угла – получим новый (двойственный или полярный к данному) трехгранный угол с плоскими углами 
и двугранными 
. Применим 1-ю теорему косинусов.
Без доказательства дается
Теорема 37. Сумма плоских углов многогранного угла меньше .
Понятие многогранника. Призма
Определение. Геометрическая фигура, ограниченная поверхностью, составленной из многоугольников, называется многогранником. Сама ограничивающая фигуру поверхность также называется многогранником.
Составляющие многогранник многоугольники называются гранями, их стороны - ребрами, концы ребер - вершинами многогранника. Отрезок, соединяющий две вершины многогранника, не принадлежащие одной грани, называется диагональю многогранника.
Определение. Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой своей грани.
|
|
|
Каждая вершина выпуклого многогранника является вершиной некоторого многогранного угла, поэтому для плоских углов при вершине справедлива теорема 36.
Определение. Призма - многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами, а остальные грани - параллелограммы.
Таким образом призма - это многогранник, у которого плоскости двух граней параллельны, а остальные граней - параллеллограммы.
Грани, лежащие в параллельных плоскостях призмы, называются основаниями, остальные грани - боковыми гранями, ребра боковых граней, не принадлежащие основаниям, - боковыми ребрами призмы.
Призма, основаниями которой являются n-угольники, называется n-угольной.
В соответствии с этим определением, параллелепипед - это призма, основаниями которой являются параллелограммы.
Определение. Длина общего перпендикуляра к основаниям называется высотой призмы.
Призма, в которой боковые ребра перпендикулярны основаниям, называется прямой. Призма, не являющаяся прямой, называется наклонной.
Прямая призма называется правильной, если ее основаниями являются правильные многоугольники.
Определение. Полной поверхностью призмы называется сумма площадей всех ее граней. Боковой поверхностью призмы называется сумма площадей ее боковых граней.
Ясно, что Sполн. = 2Sосн. + Sбок.
Теорема 38. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Доказательство. Очевидно.
Определение. Перпендикулярным сечением призмы называется сечение, перпендикулярное боковому ребру.
Теорема 39. Боковая поверхность призмы равна произведению периметра перпендикулярного сечения на боковое ребро.
Доказательство. Очевидно.
|
|
|
