Теоремы о плоскости, перпендикулярной к данной прямой, и о прямой, перпендикулярной к данной плоскости

Теоремы о плоскости, перпендикулярной к данной прямой, и о прямой, перпендикулярной к данной плоскости

 

Теорема 21. Если две плоскости  и  перпендикулярны к одной и той же прямой l, то  и  параллельны.

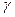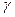Доказательство. Прямая l пересекает плоскость  в некоторой точке A, а плоскость  - в точке B. Проведем через точку A в плоскости  произвольную прямую m, перпендикулярную l. Плоскость , проходящая через прямые l и m, пересечет  по какой-то прямой m₁; так как l , то l m₁; в плоскости  прямые m и m₁ перпендикулярны одной и той же прямой l, поэтому m||m₁. 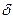Аналогично: проведем через A еще одну прямую n l; плоскость , проходящая через l и n, не совпадает с  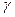и пересекает  по прямой n₁||n. В плоскостях  и  нашли две пары пересекающихся и попарно параллельных прямых (m и m₁, n и n₁), поэтому эти плоскости параллельны (теорема 13).

 

Теорема 22. Через любую точку A пространства проходит одна и только одна плоскость , перпендикулярная к данной прямой l.

Доказательство. Проведем через точку A прямую m, параллельную l (если A не лежит на l). В силе теоремы 18, достаточно доказать теорему для точки A и прямой m. Проведем через прямую m произвольную плоскость  и в ней построим прямую AB, перпендикулярную m. Пусть X - точка пространства, не лежащая в плоскости  (такая существует, по аксиоме А4 стереоматрии); проведем через нее и прямую m плоскость 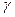 (теорема 1) и в этой плоскости прямую AC, перпендикулярную m. Прямые AB и AC пересекаются в точке A (плоскости  и 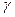 не совпадают) и определяют некоторую плоскость  (теорема 2). В плоскости  есть две пересекающиеся прямые AB и AC, перпендикулярные прямой m; по теореме 20, плоскость  и прямая m перпендикулярны. Если бы имелась еще одна плоскость 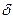, не совпадающая с  и перпендикулярная прямой m, то, по теореме 21,  и 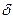 были бы параллельны, но это невозможно, поскольку они имеют общую точку A. Теорема доказана.

 

Теорема 23. Через любую точку A пространства проходит одна и только одна прямая l, перпендикулярная к данной плоскости .

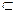
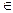
Доказательство. Рис. А50. Пусть m , m, A ; n= . В  через A проведем прямую l n. Тогда l . Единственность следует из теоремы 19.

 

 

Расстояние от точки до плоскости. Перпендикуляр и наклонная к плоскости

 

Определение. Пусть  - плоскость, A - точка, не принадлежащая плоскости . По теореме 23 через точку A можно провести прямую l=AH, перпендикулярную  (H 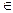). Сделаем это. Точка H называется ортогональной проекцией точки A на плоскость . Отрезок AH называется перпендикуляром к плоскости из точки A, точка H - основанием перпендикуляра. Пусть 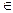B , B H. Отрезок AB называется наклонной, проведенной к плоскости  из точки A, точка B - основанием наклонной AB. Отрезок BH называется проекцией наклонной AB на плоскость .

 

Перпендикуляр из данной точки к плоскости меньше любой наклонной, проведенной из этой же точки к той же плоскости.

 

Определение. Длина перпендикуляра AH, проведенного из точки A к плоскости , называется расстоянием от точки A до плоскости

 

Теорема 24 (большая). Если из некоторой точки A пространства проведены к плоскости  перпендикуляр AH и наклонные AB и AC, то:

1) если BH=CH, то AB=AC;

2) если BH> CH, то AB> AC;

3) если AB=AC, то BH=CH;

4) если AB> AC, то BH> CH.

(Две наклонные, имеющие равные проекции, равны; из двух наклонных больше та, проекция которой больше; равные наклонные имеют равные проекции; из двух проекций та больше, которая соответствует большей наклонной).

Доказательство сводится к рассмотрению соответствующих прямоугольных треугольников.

 

Ортогональная проекция точки, отрезка, прямой, фигуры. Угол между

прямой и плоскостью

 

Определение. Ортогональной проекцией точки A на плоскость  называется основание перпендикуляра, опущенного из точки A на плоскость .

Ортогональной проекцией фигуры F на плоскость  называется фигура F' плоскости , точками которой являются ортогональные проекции на эту плоскость точек фигуры F.

 

Теорема 25. Проекция прямой есть прямая, проекцией отрезка является отрезок.

 

Пересекающиеся прямые l и m проектируются в прямые l' и m', пересекающиеся в точке A', которая является проекцией точки A пересечения прямых l и m.

Ортогональные проекции параллельных прямых есть параллельные прямые.

 

Определение. Углом между прямой l и плоскостью  называется (не более, чем прямой! ) угол между прямой l и ее проекцией l' на плоскость .

Принято считать, что угол между прямой, параллельной плоскости, и этой плоскостью равен 0; угол между прямой, перпендикулярной плоскости, и этой плоскостью равен .

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: