Призма. Несколько задач

Призма. Несколько задач

1. Докажите, что сумма двугранных углов при всех боковых ребрах n-угольной призмы равна .

Решение. Нужно рассмотреть перпендикулярное сечение призмы!

2. Длины всех ребер правильной треугольной призмы ABCA₁B₁C₁ равны a. Постройте общий перпендикуляр прямых AA₁ и BC₁ и вычислите его длину. Найдите угол между AA₁ и BC₁.

Решение.  (AH и A₁H₁ - высоты треугольников ABC и A₁B₁C₁. . Отрезок MN, параллельный AH, - искомый перпендикуляр. Его длина равна . Угол между AA₁ и BC₁ равен углу между HH₁ и BC₁ и равен .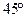

3. Сторона основания правильной треугольной призмы ABCA₁B₁C₁ равна a. Диагональ AC₁ ее боковой грани образует с другой боковой гранью ABB₁ угол j. Найдите боковую поверхность призмы.

Решение. Угол C₁AD₁, где CD₁ - медиана треугольника A₁B₁C₁, - угол AC₁ с плоскостью ABB₁. Ответ. .

4. Нижнее основание прямой призмы ABCDA₁B₁C₁D₁ - ромб ABCD с острым углом j. Известно, что в эту призму можно вписать шар диаметра d. Найдите площадь сечения призмы плоскостью, проходящей через ребра BC и A₁D₁.

Решение. d/2 - радиус окружности, вписанной в ромб ABCD. DK=d - высота ромба. Тогда DC = d / sin j, DD₁=d. S = BC × D₁K, где D₁K - высота параллелепипеда A₁D₁CB. .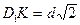

Ответ. .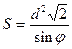

5. Найдите площадь полной поверхности призмы, описанной около сферы, если площадь ее основания равна S.

Решение. S = pr (p - полупериметр основания, r - радиус сферы), S_бок = 4pr, поэтому

Ответ. 6S.

Серия пособий А. И. Маринина включает также брошюры:

Трехгранный угол

Задачи по геометрии-10 (с решениями)

Исследование квадратного трехчлена

Задачи по геометрии-9