Углы с сонаправленными сторонами

Углы с сонаправленными сторонами

 

Определение. Два луча AB и CD называются сонаправленными, если они лежат в одной плоскости  и векторы AB и CD коллинеарны с положительным коэффициентом пропорциональности. Иначе: лучи AB и CD, не лежащие на одной прямой, называются сонаправленными, если точки B и D находятся в одной и той же из двух полуплоскостей, на которые прямая AC разбивает плоскость , содержащую прямые AB и CD (параллельными прямыми AB и CD такая плоскость, по теореме 3, однозначно определяется); если же лучи AB и CD лежат на одной прямой, они являются сонаправленными, когда векторы AB и CD имеют одинаковое направление.

Два угла со сторонами, являющимися попарно сонаправленными лучами, называются углами с соответственно сонаправленными сторонами.

 

Важность понятия сонаправленности двух лучей проясняется следующим фактом:

Теорема 12. Если стороны двух углов соответственно сонаправлены, то эти углы равны.

Доказательство. См. А(стр. 16-17).

 

Угол между скрещивающимися прямыми

 

Определение. Две пересекающиеся прямые образуют две пары вертикальных углов. Углом между такими прямыми называется наименьший из этих углом, то есть острый или прямой угол в получившейся конфигурации прямых.

 

Определение. Пусть l и m - скрещивающиеся прямые. Если A - произвольная точка пространства, l₁ и m₁ - прямые, проходящие через A и параллельные соответственно l и m, то углом между скрещивающимися прямыми l и m называется угол между (пересекающимися) прямыми l₁ и m₁.

 

Замечание 1. Величина угла между прямыми l и m не зависит от выбора точки A.

Доказательство. Пусть B - некоторая другая точка пространства, l₂ и m₂ - две прямые, проходяшие через B так, что l₂||l, m₂||m. В силу того, что l₁||, m₁||m, имеем l₂||l₁ и m₂||m₁, стало быть, угол между l₁ и m₁ и угол между l₂ и m₂ имеют соответственно сонаправленные стороны (поскольку мы выбираем наименьшие из двух пар смежных углов между l₁ и m₁ и между l₂ и m₂), поэтому эти углы равны по теореме 12.

 

Замечение 2. Часто удобно в качестве точки A выбирать точку на одной из заданных скрещивающихся прямых.

 

 

Параллельность плоскостей. Признак и свойства параллельных плоскостей

 

Определение. Две плоскости  и  называются параллельными, если они не имеют общих точек.

Обозначение: || .

 

Теорема 13 (признак параллельности плоскостей). Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.

Доказательство. Пусть пересекающиеся в точке A прямые AB и AC плоскости  параллельны соответственно прямым A'B' и A'C' плоскости . Тогда AB|| , AC||  (теорема 8). Пусть плоскости  и  пересекаются и l - прямая их пересечения, тогда l||AB и l||AC (теорема 9); получили, что в плоскости  через точку A проходят две прямые AB и AC, параллельные одной и той же прямой l - противоречие, и плоскости  и  не пересекаются, то есть параллельны.

 

Приведем два свойства параллельных плоскостей.

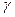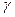
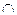
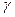
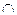
Теорема 14. Если две параллельные плоскости  и  пересечены третьей плоскостью , то прямые l=  и m=  их пересечения параллельны.

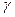
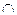
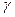
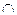
Доказательство. Имеем || , =l, =m; прямые l и m не пересекаются, иначе точка их пересечения была бы общей для параллельных плоскостей  и , и принадлежат одной плоскости 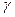, следовательно, l||m, ч. т. д.

 

Теорема 15. Отрезки параллельных прямых AB и CD, заключенные между параллельными плоскостями, равны.

Доказательство. Прямые AB и CD содержатся в некоторой плоскости 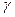 (теорема 3); по предыдущему свойству, прямые AC и BD параллельны, поэтому четырехугольник ABDC - параллелограмм, и его противоположные стороны равны: AB=CD.

 

Тетраэдр и его изображение на плоскости

 

Определение. Пусть дан треугольник ABC и точка D, не лежащая в плоскости этого треугольника. Геометрическая фигура, ограниченная плоскостями ABC, DAB, DAC и DBC, называется тетраэдром ( треугольной пирамидой ) DABC.

Треугольники ABC, DAB, DAC, DBC называются гранями, стороны этих треугольников AB, BC, CA, DA, DB, DC - ребрами, вершины треугольников A, B, C, D - вершинами тетраэдра ABCD.

 

Таким образом, тетраэдр имеет 4 вершины, 6 ребер и 4 грани. Заметим на будущее, что величина e = (количество вершин - количество ребер + количество граней) = 2.

 

Ребра тетраэдра, не имеющие общих точек, называются противоположными.

Противоположные ребра тетраэдра скрещиваются.

 

Иногда выделяют одну из четырех граней тетраэдра, ее именуют основанием, другие грани - боковыми гранями тетраэдра.

 

Изображение тетраэдра на плоскости.

1. Невидимые (скрытые) ребра изображаются пунктиром.

2. Введем на плоскости прямоугольную систему координат.

3. Отметим точки A(0; 0) и B(12; 0) - ребро AB. Соединим точки A и B пунктирной линией (это будет невидимым ребром AB).

4. Отметим точку C(3, 5; -5) и соединим ее сплошными линиями с точками A и B - получим ребра CA и CB.

5. Отметим точку D(7; 7) и соединим ее с точками A, B и C сплошными линиями - получим " каркас" тетраэдра DABC.

6. При таком взаимном расположении точек A, B, C, D хорошо видны все вершины, ребра и грани тетраэдра.

7. Приблизительно таким заданием вершин следует руководствоваться при построении чертежей, решая геометрические задачи на тетраэдр.

 

 

Параллелепипед и его изображение на плоскости

 

Определение. Пусть даны два равных параллелограмма ABCD и A₁B₁C₁D₁ в параллельных плоскостях ABCD и A₁B₁C₁D₁ так, что четырехугольники AA₁B₁B, AA₁D₁D, BB₁C₁C, DD₁C₁C- параллелограммы. Геометрическая фигура, ограниченная плоскостями ABCD, A₁B₁C₁D₁, AA₁B₁B, AA₁D₁D, BB₁C₁C и DD₁C₁C, называется параллелепипедом ABCDA₁B₁C₁D₁. Ограничивающие параллелепипед пераллелограммы ABCD, A₁B₁C₁D₁, AA₁B₁B, AA₁D₁D, BB₁C₁C, DD₁C₁C называются гранями, стороны AB, BC, CD, DA, A₁B₁, B₁C₁, C₁D₁, D₁A₁, AA₁, BB₁, CC₁, DD₁ этих параллелограммов - ребрами, вершины A, B, C, D, A₁, B₁, C₁, D₁ - вершинами параллелепипеда ABCDA₁B₁C₁D₁.

 

Параллелепиипед имеет 8 вершин, 12 ребер и 6 граней. Заметим на будущее, что что величина e = (количество вершин - количество ребер + количество граней) = 2.

 

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие - противоположными. Две вершины, не принадлежащие одной грани, называются противоположными. Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины. Параллелепипед имеет 4 диагонали.

 

Задание: укажите смежные и противоположные грани, противоположные вершины и диагонали параллелепипеда.

 

Иногда выделяют две противоположные грани параллелепипеда, и их именуют основаниями, а другие грани - боковыми, при этом принадлежащие боковым граням ребра, не лежащие в плоскостях оснований, называют боковыми.

 

Изображение параллелепипеда на плоскости.

1. Невидимые (скрытые) ребра изображаются пунктиром.

2. Введем на плоскости прямоугольную систему координат.

3. Отметим точки A(0; 0), B(3; 3), C(12; 3), D(9; 0), A₁(2; 8), B₁(5; 11), C₁(14; 11), D₁(11; 8) - вершины параллелепипеда ABCDA₁B₁C₁D₁. Изобразим ребра AB, BC, CD, DA, A₁B₁, B₁C₁, C₁D₁, D₁A₁, AA₁, BB₁, CC₁ и DD₁ (при этом ребра AB, BC, BB₁ будут невидимыми). Невидимые ребра изображаются пунктирной линией.

5. Получим " каркас" параллелепипеда ABCDA₁B₁C₁D₁.

6. При таком взаимном расположении точек A, B, C, D, A₁, B₁, C₁, D₁ хорошо видны все вершины, ребра и грани параллелепипеда.

7. Приблизительно таким заданием вершин следует руководствоваться при построении чертежей, решая геометрические задачи на параллелепипед.

 

 

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: