 |
Задание 13 Профильного ЕГЭ по математике. Стереометрия
|
|
|
|
Задание 13 Профильного ЕГЭ (Стереометрия) многие старшеклассники считают самой сложной задачей в варианте. И напрасно! Ничего особенного в ней нет. Просто начинать надо вовремя, лучше всего в десятом классе. И конечно, не с самых сложных задач. Действуем по порядку!
1. Подготовительный этап — решение задач по стереометрии из первой части ЕГЭ. Повторите формулы объемов и площадей поверхности многогранников и тел вращения. Посмотрите, как решаются типовые задачи.
2. Повторите необходимую теорию. Вот краткая Программа по стереометрии. Проверьте себя. Все ли вы знаете? В освоении стереометрии вам поможет наш ЕГЭ-Справочник.
3. Посмотрите, как правильно строить чертежи.
4. Выучили теорию? Применяем на практике — строим сечения.
5. Решаем простые задачи по стереометрии. И после этого — переходим к реальным задачам ЕГЭ.
6. Задачи 13 по стереометрии из Профильного ЕГЭ по математике обычно относятся к одному из типов. Смотрите нашу Классификацию задач по стереометрии и методы их решения.
Вот примеры простых подготовительных задач по стереометрии:
1. Высота правильной треугольной пирамиды равна 4, а угол между боковой гранью и плоскостью основания равен 60 градусов. Найдите расстояние от вершины основания до плоскости противолежащей ей боковой грани.
Посмотреть решение
2. В правильной шестиугольной призме 
, все ребра которой равны 1, точка G — середина ребра 
Найдите угол между прямой АG и плоскостью 
Посмотреть решение
3. В правильной шестиугольной призме 
все рёбра равны 1. Найдите расстояние от точки В до плоскости 
Посмотреть решение
4. В основании прямой призмы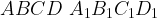 
лежит ромб. Найти угол между прямыми 
и 
Посмотреть решение
|
|
|
5. Точка E — середина ребр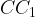а 
куба 
Найдите угол между прямыми 
и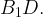 
Посмотреть решение
6. В правильной треугольной призме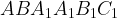 
, все рёбра которой равны 
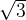, найдите расстояние между прямыми 
и 
Посмотреть решение
7. Радиус основания конуса с вершиной P равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки A и B, делящие окружность на две дуги, длины которых относятся как 1: 5. Найдите площадь сечения конуса плоскостью ABP.
Посмотреть решение
А теперь — реальные задачи по стереометрии, встретившиеся выпускникам на Профильном ЕГЭ по математике.
8. Точки М и N — середины ребер соответственно АВ и СD треугольной пирамиды АВСD, О — точка пересечения медиан грани АВС.
а) Докажите, что прямая DO проходит через середину отрезка MN.
б) Найдите угол между прямыми MN и ВС, если АВСD — правильный тетраэдр.
Посмотреть решение
9. В цилиндре образующая перпендикулярна плоскости основания. На окружности одного из оснований цилиндра выбраны точки A, B и C, а на окружности другого основания — точка 
, причём 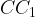— образующая цилиндра, а AC — диаметр основания. Известно, что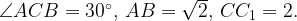 
а) Докажите, что угол между прямыми 
и 
равен 
б)Найдите объём цилиндра.
Посмотреть решение
10. В основании призмы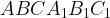 
лежит правильный треугольник, вершина проецируется в центр Q основания АВС.
а) Докажите, что плоскости 
и 
перпендикулярны,
б) Найдите угол между прямой и плоскостью 
если боковое ребро призмы равно стороне основания.
Посмотреть решение
11.
Сечением прямоугольного параллелепипеда 
плоскостью 
, содержащей прямую 
и параллельной прямой АС, является ромб.
а) Докажите, что грань ABCD — квадрат.
б) Найдите угол между плоскостями и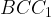 
, если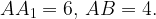 
Посмотреть решение
12. На ребрах АВ и ВС треугольной пирамиды АВСD отмечены точки М и N соответственно, причем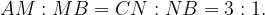 
Точки P и Q — середины ребер DA и DC соответственно.
а) Докажите, что точки P, Q, M и N лежат в одной плоскости.
|
|
|
б) Найдите, в каком отношении эта плоскость делит объем пирамиды.
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 14
7 лайфхаков для решения задач по стереометрии:
1. Задача по стереометрии не решается без хорошего чертежа! Чертеж строим по линейке, черной ручкой, на клетчатой бумаге, по правилам построения чертежей. На ЕГЭ можно и нужно пользоваться линейкой! А бланк будет в клеточку.
2. Все, что нужно, на чертеже должно быть хорошо видно! Если вам не понравился чертеж — не сидите над ним, бросьте и нарисуйте другой. Одного объемного чертежа будет недостаточно — понадобится один или несколько плоских.
|
|
|
