 |
Степенные уравнения и неравенства
|
|
|
|
Степенные уравнения и неравенства
Тема для повторения: Степенная функция
6. При адиабатическом процессе для идеального газа выполняется закон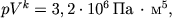 
где 
— давление в газе в паскалях, V — объeм газа в кубических метрах, 
Найдите, какой объём 
(в куб. м) будет занимать газ при давлении , равном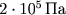 
.
Подставим данные в уравнение 
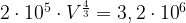
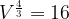
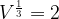
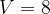
Показательные уравнения и неравенства
Темы для повторения:
Показательная функция.
Показательные неравенства.
7. Уравнение процесса, в котором участвовал газ, записывается в ви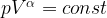де 
, где (Па) — давление в газе, — объём газа в кубических метрах, 
— положительная константа. При каком наименьшем значении константы уменьшение вдвое раз объёма газа, участвующего в этом процессе, приводит к увеличению давления не менее, чем в 4 раза?
Согласно понятиям термодинамики, в каждом состоянии газ характеризуется определенными параметрами — давлением, объемом, температурой. По условию задачи, газ переходит из одного состояния в другое так, что 
Это значит, что
Объем уменьшился вдвое, то есть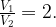 
Поскольку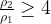 
, получим, что 
Тогда 
Наименьшее значение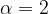 
записываем в ответ.
Логарифмические уравнения и неравенства
Темы для повторения:
Логарифмы.
Логарифмические неравенства.
8. Водолазный колокол, содержащий 
моля воздуха при давлении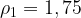 
атмосферы, медленно опускают на дно водоёма. При этом происходит изотермическое сжатие воздуха до конечного давления 
Работа, совершаемая водой при сжатии воздуха, определяется выражением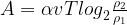 
, где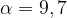 
— постоянная, 
— температура воздуха. Найдите, какое давление 
(в атм) будет иметь воздух в колоколе, если при сжатии воздуха была совершена работа в 29100 Дж.
|
|
|
Подставим все данные в уравнение для совершенной водой работы:
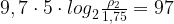
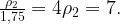
Тригонометрические уравнения и неравенства
Темы для повторения: Тригонометрия
9. При нормальном падении света с длиной волны 
нм на дифракционную решeтку с периодом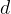 
нм наблюдают серию дифракционных максимумов. При этом острый угол 
(отсчитываемый от перпендикуляра к решётке), под которым наблюдается максимум, и номер максимума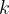 
связаны соотношением 
. Под каким минимальным углом (вградусах) можно наблюдать третий максимум на решeтке с периодом, не превосходящим 2400 нм?
Запишем условие задачи в виде неравенства. Заметим, что нам нужен третий максимум, то есть номер максимума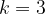 
.
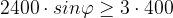
Поскольку угол — острый, 
Ответ: 30.
Это была простая задача по тригонометрии. А закончим мы самыми сложными, какие только могут встретиться в этой теме, - тригонометрическими неравенствами.
10. Груз массой 0, 08 кг колеблется на пружине со скоростью, меняющейся по закону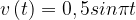 
, где 
— время в секундах. Кинетическая энергия груза, измеряемая в джоулях, вычисляется по формуле 
, где 
— масса груза (в кг), - скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 5 
Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
. Применим формулу понижения степени:
Нарисуем график функци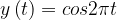и 
при 
Значения этой функции не больше нуля ровно половину времени из первой секунды.
Ответ: 0, 5.
11. Груз массой 0, 25 кг колеблется на пружине со скоростью, меняющейся по закону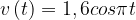 
, где — время в секундах. Кинетическая энергия груза вычисляется по формуле , где — масса груза (вкг),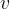 
— скорость груза (вм/с). Определите, какую долю времени из первой секунды после начала движения кинетическая энергия груза будет не менее 
Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.
|
|
|
По формуле понижения степени,
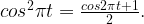Отсюда
Построим график функции 
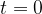при
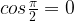(при 
)
(при 
)
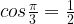(при 
)
(при 
)
(при 
)
(при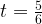 
)
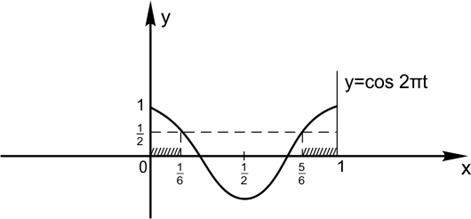
Найдем, каждую часть из первой секунды выполняется неравенство
Получим, что 
при на 
и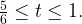 
Вместе эти отрезки составляют 
от первой секунды; 
Ответ: 0, 33.
Кому-то удобнее рисовать в этой задаче не график, а тригонометрический круг. Это дело вкуса. Главное — не решать тригонометрические неравенства в уме. И конечно, внимательно читать и анализировать условие: -)
Задание 8
Задание 8 Профильного ЕГЭ по математике – это несколько типов текстовых задач. Условия и «сюжеты» задач могут быть разными. При этом в каждой из них нужно построить математическую модель, то есть обозначить какие-либо величины за переменные, составить уравнение и решить его. И еще есть неочевидные секреты их решения. О них – в конце статьи.
Вот основные типы текстовых задач, которые могут вам встретиться на ЕГЭ под номером 8. Переходите по ссылкам, читайте краткую теорию и разбирайте вместе с нами решения задач!
|
|
|
