 |
1. Задачи на движение. 6. Задачи на нахождение средней скорости. 7. Задачи на движение протяженных тел, встречное движение и обгон
|
|
|
|
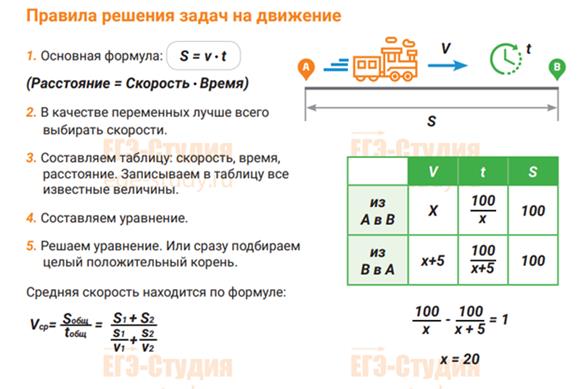
1. Задачи на движение
 2. Задачи на работу
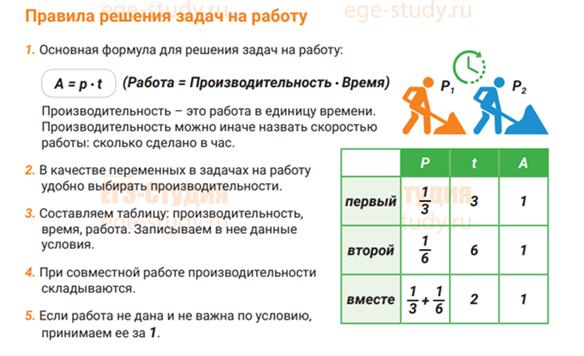
2. Задачи на работу
 3. Задачи на проценты
3. Задачи на проценты
 4. Задачи на сплавы, смеси, растворы
4. Задачи на сплавы, смеси, растворы
 5. Задачи на движение по окружности
5. Задачи на движение по окружности
Формула  работает и в этом случае. Здесь
работает и в этом случае. Здесь  – расстояние,
– расстояние, 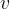 – скорость,
– скорость,  – время.
– время.
А секрет задач на движение по окружности: тот, кто обгоняет, проезжает на 1 круг больше, если это первый обгон. И на n кругов больше, если обогнал другого в  -ный раз.
-ный раз.
6. Задачи на нахождение средней скорости
По определению, средняя скорость получается, если всё расстояние поделить на всё время. В общем случае она не равна среднему арифметическому скоростей, а находится по следующей формуле:

7. Задачи на движение протяженных тел, встречное движение и обгон
Да, это те самые задачи, где поезд проходит через туннель. Или проезжает мимо платформы. И нам нужно учитывать длину поезда.
Есть еще задачи на встречное движение или обгон. Например, два поезда движутся навстречу друг другу (конечно, по параллельным путям), или один поезд обгоняет другой. Такие задачи удобно решать в движущейся системе отсчета.
Но и это не все. Есть еще задачи ЕГЭ на арифметическую и геометрическую прогрессии.
 8. Задачи на арифметическую прогрессию
8. Задачи на арифметическую прогрессию
Арифметическая прогрессия в задачах ЕГЭ по математике
9. Задачи на геометрическую прогрессии
Геометрическая прогрессия в задачах ЕГЭ по математике
И еще мы обещали секреты решения текстовых задач на движение и работу. Читайте и применяйте!
Задание 9
В 2022 году в вариантах ЕГЭ Профильного уровня появилась задание №9 по теме «Графики функций». Можно считать его подготовительным для освоения задач с параметрами.
Как формулируется задание 9 ЕГЭ по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
|
|
|
Чтобы выполнить это задание, надо знать, как выглядят и какими свойствами обладают графики элементарных функций. Надо уметь читать графики, то есть получать из них необходимую информацию. Например, определять формулу функции по ее графику.
Вот необходимая теория для решения задания №9 ЕГЭ.
Что такое функция
Чтение графика функции
Четные и нечетные функции
Периодическая функция
Обратная функция
5 типов элементарных функций и их графики
Преобразование графиков функций
Построение графиков функций
Да, теоретического материала здесь много. Но он необходим — и для решения задания 9 ЕГЭ, и для понимания темы «Задачи с параметрами», а также для дальнейшего изучения математики на первом курсе вуза.
Рекомендации:
Запоминай, как выглядят графики основных элементарных функций. Замечай особенности графиков, чтобы не перепутать параболу с синусоидой: -)
Проверь себя: какие действия нужно сделать с формулой функции, чтобы сдвинуть ее график по горизонтали или по вертикали, растянуть, перевернуть?
Разбирая решения задач, обращай внимание на то, как мы ищем точки пересечения графиков или неизвестные переменные в формуле функции. Такие элементы оформления встречаются также в задачах с параметрами.
Задание 9 в формате ЕГЭ-2021
Линейная функция
Необходимая теория
1. На рисунке изображён график функции 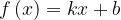 . Найдите значение
. Найдите значение  , при котором
, при котором 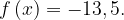

Решение:
Найдем, чему равны k и b. График функции проходит через точки (3; 4) и (-1; -3). Подставив по очереди координаты этих точек в уравнение прямой y = kx + b, получим систему:

Вычтем из первого уравнения второе:
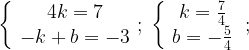
Уравнение прямой имеет вид:
|
|
|

Найдем, при каком  значение функции равно -13, 5.
значение функции равно -13, 5.


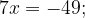

Ответ: -7.
2. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:
Запишем формулы функций.
Одна из них проходит через точку (0; 1) и ее угловой коэффициент равен -1. Это линейная функция 
Другая проходит через точки (-1; -1) и (-2; 4). Подставим по очереди координаты этих точек в формулу линейной функции 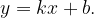

Вычтем из первого уравнения второе.
 тогда
тогда 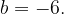
Прямая задается формулой: 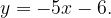
Найдем абсциссу точки пересечения прямых. Эта точка лежит на обеих прямых, поэтому:
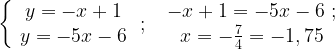
Ответ: -1, 75.
3. На рисунке изображены графики двух линейных функций. Найдите абсциссу точки пересечения графиков.

Решение:
Прямая, расположенная на рисунке ниже, задается формулой  так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
так как ее угловой коэффициент равен 1 и она проходит через точку (-3; -2).
Для прямой, расположенной выше, угловой коэффициент равен 
Эта прямая проходит через точку (-2; 4), поэтому: 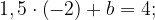
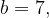 эта прямая задается формулой
эта прямая задается формулой 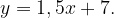
Для точки пересечения прямых:
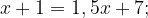


Ответ: -12.
|
|
|


