 |
Парабола и квадратные неравенства
|
|
|
|
Темы для повторения:
Квадратичная функция
Квадратичные неравенства
3. Зависимость объёма спроса 
(единиц в месяц) на продукцию предприятия-монополиста от цены 
(тыс. руб. ) задаётся формулой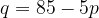 
. Выручка предприятия за месяц 
(в тыс. руб. ) вычисляется по формуле 
. Определите наибольшую цену , при которой месячная выручка 
составит не менее 210 тыс. руб. Ответ приведите в тыс. руб.
Здесь точно придется читать условие. И решать именно неравенство, а не уравнение.
Поскольку месячная выручка не менее 210 тысяч рублей,
График функции в левой части неравенства — квадратичная парабола с ветвями вниз.
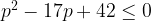
Заметим, что это неравенство не превращается в уравнение 
. Уравнение здесь нужно для того, чтобы найти, при каких значениях выручка равна 210. Решив его, получим: 
или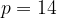 
. Решения неравенства:
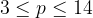
Наибольшее значение равно 14.
Ответ: 14.
- «Отлично, - скажете вы. Берем больший из корней квадратного уравнения, и готово». Так ли это? - Конечно, нет. Надо внимательно прочитать условие и понять, что же будет ответом задачи.
4. Выcота над землёй подброшенного вверх мяча меняетcя по закону 
, где 
— выcота в метрах, 
- время в cекундах, прошедшее c момента броcка. Cколько cекунд мяч будет находитьcя на выcоте не менее трёх метров?
Запишем, что 
Построим график функции в левой части — то есть зависимость высоты мяча от времени.
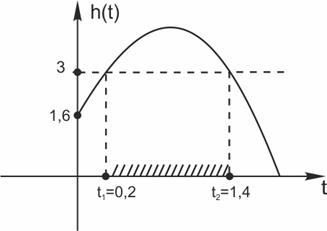
Мы видим, что через 
секунд после начала полёта мяч оказался на высоте 3 метра. Мяч продолжал лететь вверх, высота увеличивалась. Затем началось снижение, высота уменьшалась, и в момент времени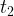 
снова стала равна трём метрам над землей. Получается, что мяч находился на высоте не менее трёх метров в течение 
секунд.
|
|
|
Осталось найти разность 
Для этого решим квадратичное неравенство 
Работать с дробными коэффициентами неудобно. Умножим обе части неравенства на 5:
Найдем корни соответствующего уравнения 
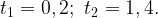
Разность 
Ответ: 1, 2.
Вот еще одна задача из первой части варианта профильного ЕГЭ, в которой больше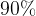 
решающих получают неправильный ответ. Только потому, что не пользуются графиком.
5. Завиcимоcть температуры (в градуcах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экcпериментально и на иccледуемом интервале температур определяетcя выражением 
, где - время в минутах, 
K, 
K/мин,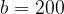 
K/мин. Извеcтно, что при температуре нагревателя cвыше 1760 K прибор может иcпортитьcя, поэтому его нужно отключать. Определите, через какое наибольшее время поcле начала работы нужно отключать прибор. Ответ выразите в минутах.
Решите самостоятельно. Какой ответ у вас получился?
По условию, зависимость температуры нагревательного элемента от времени определяется формулой:
В нормальном режиме работы прибора должно выполняться неравенство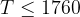 
, или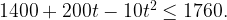 
Нарисуем график зависимости температуры нагревателя от времени:
. Это квадратичная парабола с ветвями вниз.
Мы включаем прибор в момент времени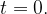 
Температура нагревателя повышается и в момент времени достигает 1760 К. Если в этот момент прибор не выключить, температура продолжает повышаться. Но это значит, что прибор испортится, то есть сгорит! Ясно, что отключать его надо в момент времени 
Осталось найти Решим квадратичное неравенство: 
Корни соответствующего квадратного уравнения: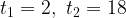 
Мы нашли, что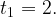 
Ответ: 2.
Ну как? Вы все еще считаете, что условие можно не читать? : -)
Квадратичные функции в задании №7 Профильного ЕГЭ — это еще не всё. Впереди степенные, показательные, логарифмические и тригонометрические уравнения и даже неравенства.
|
|
|
