 |
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
|
|
|
|
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
- Если в задаче с параметром можно сделать замену переменной — сделайте замену.
- Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:
Задача 1. При каких значениях a системы 
и 
равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При 
— системы равносильны, так как обе не имеют решений
2) При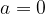 
— второе уравнение имеет решение 
которое является решением первой системы.
3) При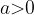 
Система уравнений
Уравнение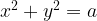 
задает окружность с центром в начале координат и радиусом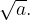 
Решениями системы
являются две точки, в которых прямая 
пересекает окружность, заданную уравнением 
А вот уравнение 
задает семейство параллельных прямых 
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением 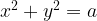, пересекала только одну из этого семейства прямых, а именно прямую , и не имела общих точек с другими прямыми из этого семейства.
Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса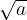 
не имела общих точек с прямыми, параллельными прямой , то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
|
|
|
Когда же происходит касание в точках A и B?
В случае касания радиус окружности 
Мы легко находим это из треугольника прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания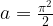 
, а если 
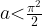— касания не происходит.
Объединяя случаи, получим, что системы равносильны, если 
Легко? Если справились — вот еще одна интересная задача:
Задача 2. При каких значениях параметра a найдется такое значение параметра 
, что система уравнений 
имеет ровно три различных решения?
Вот решение этой задачи.
Задание 18
по Математике
Вот она! Загадочная. Нестандартная. Задача 18 Профильного ЕГЭ по математике.
Эта задача оценивается в целых 4 первичных балла, и они пересчитываются в 9-10 тестовых.
Можно ничего не знать. И удачно подобрать пример. И получить 1 балл за пункт (а). Во всяком случае, попробовать это сделать.
А можно потратить 2 часа на перебор вариантов… и так ничего и не найти. Если не знаешь секретов решения этой задачи. ОК, некоторые из секретов мы расскажем.
Действительно, пункт (а) в задаче 18 почти всегда решается сразу. Пункт (б) тоже решается быстро, но только если повезет. Пункт (в) без специальной подготовки решить невозможно.
Необходимая теория для решения задач на числа и их свойства - это всего две страницы. Делимость чисел, наибольший общий делитель и наименьшее общее кратное, основная теорема арифметики, признаки делимости на 3, на 4, на 5, на 8, 9, 10 и 11. Ничего сложного.
Повторите также темы: Арифметическая прогрессия и Геометрическая прогрессия
Начинать лучше всего с подготовительных задач.
Затем стоит освоить метод «Оценка плюс пример». Для того чтобы применить этот метод, от строгих оценок, которые даны в условии (со знаками > или < ), переходим к нестрогим (со знаками ≥ или ≤ ).
|
|
|
Узнать о секретах решения задания 18 Профильного ЕГЭ по математике.
Узнать больше о решении уравнений в целых числах. В школьных учебниках этого нет.
Один из необходимых навыков для решения пункта (в) – работа с неравенствами. В школьных учебниках этого тоже нет.
Многие считают, что если в этой задаче в пункте (а) ответ «да», то во втором обязательно должно быть «нет». Авторитетно заявляем: нет, необязательно! Может быть любое сочетание из «да» и «нет». И может быть «да» в обоих пунктах, и «нет» в обоих.
Если вопрос в этой задаче (неважно, в каком пункте) формулируется как «Может ли быть…» - и дальше некоторое утверждение, и ваш ответ: «Да», - то одного вашего «Да» недостаточно. Нужен пример. И если вы его подберете, вы не обязаны объяснять, как нашли его.
Если ответ на этот вопрос: «Нет», то вам нужно это доказать. «Нет, потому что…» - и приводите свое доказательство.
В общем, проще показать это на примерах:
1. За прохождение каждого уровня игры на планшете можно получить от одной до трёх звёзд. При этом заряд аккумулятора планшета уменьшается на 3 пункта при получении трёх звёзд, на 6 пунктов при получении двух звёзд и на 9 пунктов при получении одной звезды. Витя прошёл несколько уровней игры подряд.
а) Мог ли заряд аккумулятора уменьшиться ровно на 32 пункта?
б) Сколько уровней игры было пройдено, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
в) За пройденный уровень начисляется 9000 очков при получении трёх звёзд, 5000 — при получении двух звёзд и 2000 — при получении одной звезды. Какое наибольшее количество очков мог получить Витя, если заряд аккумулятора уменьшился на 33 пункта и суммарно было получено 17 звёзд?
а) Заметим, что заряд аккумулятора при прохождении уровня уменьшается на 3, 6 или 9 пунктов, и все эти числа делится на 3. Поскольку 32 не делится на 3, заряд не мог уменьшиться на 32 пункта.
б) Да, на 33 пункта заряд мог уменьшиться.
Пусть на х уровнях получено по 3 звезды, на у уровнях по 2 звезды и на z уровнях по 1 звезде.
Тогда:
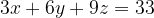, то есть 
.
Сложив уравнения и , получим, что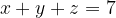 
(пройдено 7 уровней).
Системе удовлетворяют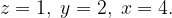 
При этом заряд аккумулятора уменьшился на 33 пункта.
в) Поскольку и 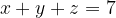, получаем, что 
. Возможны варианты:
|
|
|
, тогда 
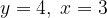, получено 47 тысяч очков.
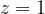, тогда 
, получено 48 тысяч очков.
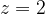, тогда 
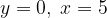, получено 49 тысяч очков – это максимально возможное количество.
Это была простая задача №18. А вот сложная.
2. В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писал 51 учащийся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 вырасти в два раза?
б) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Мог ли первоначальный балл в школе № 2 равняться 1?
в) Средний балл в школе № 1 вырос на 10%, средний балл в школе № 2 также вырос на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.
Пусть в первой школе писали тест 
учеников, а во второй 
учеников, причем
, 
.
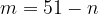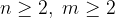Пусть учащиеся первой школы набрали в сумме 
балл, а учащиеся второй 
баллов.
Тогда средние баллы равны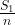 
и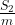 
.
Пусть из первой школы во вторую перешел ученик, набравший за тест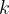 
баллов.
а) Предположим, что средний балл в школе № 1 вырос в два раза. Тогда 
.
Отсюда: 
.
Поскольку 
положительно, получаем, что 
– противоречие с условием.
Ответ в пункте (а): нет.
б) Во втором пункте ответ тоже «нет». Предположим, что 
. Получим:
.
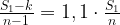
Поскольку ,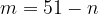
.
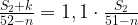Если , то 
.
Тогда:
. Отсюда:
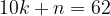. Очевидно, 
и 
.
Что будет, если 
? Тогда 
.
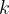Подставив эти и в уравнение
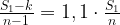, получим: 
, 
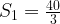, противоречие с условием, поскольку 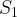– целое. Значит,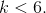 
С другой стороны, из условия 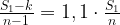получаем, что
, значит, 
.
Но если 
, то 
и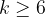 
– получили противоречие.
в) По условию, и в первой, и во второй школах первоначально средний балл был целым числом. Он не может быть равен единице (из пункта (б)). Проверим, может ли он быть равен 2, 3, 4…
Пусть первоначально средний балл равен 2. Тогда
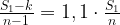
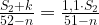
. Условие по-прежнему должно выполняться.
|
|
|
Преобразуя эти уравнения, получим:
.
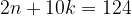
Значит,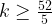 
и 
. Подходит 
и 
.
При таких значениях 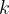уравнение имеет решения 
или 
.
Подставим поочередно пары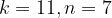 
и 
в уравнение
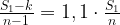, получим, что целых решений 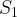это уравнение не имеет.
Пусть первоначально средний балл равен 3. Тогда
,
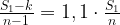
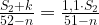
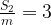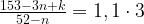
, подходит 
, тогда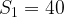 
.
Например, в первой школе тест писали 2 учащихся и набрали 22 и 18 баллов. В школе № 2 писали тест 49 учащихся и каждый набрал по три балла, а у перешедшего из одной школы в другую учащегося 18 баллов.
Да, непростая это задача, девятнадцатая из варианта ЕГЭ. Но если к ней привыкнуть, потренироваться, - то вполне можно решить и заработать необходимые на ЕГЭ баллы.
|
|
|
