 |
3. Учимся записывать решение кратко. Вспомним основные обозначения
|
|
|
|
3. Учимся записывать решение кратко. Вспомним основные обозначения
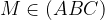 — точка M принадлежит плоскости АВС
— точка M принадлежит плоскости АВС
 — прямые а и b пересекаются в точке О
— прямые а и b пересекаются в точке О
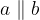 — прямые а и b параллельны
— прямые а и b параллельны
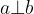 — прямые а и b перпендикулярны
— прямые а и b перпендикулярны
4. Почти в каждой задаче по стереометрии встречаются «особенные треугольники».
Давайте вспомним:
- В прямоугольном равнобедренном треугольнике гипотенуза в  раз больше катета
раз больше катета
- В треугольнике с углами 30, 60 и 90 градусов гипотенуза в 2 раза больше меньшего катета, а больший катет в 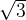 раз больше меньшего.
раз больше меньшего.
5. Формула для площади прямоугольной проекции фигуры помогает найти угол между плоскостями. Здесь
помогает найти угол между плоскостями. Здесь  — угол между плоскостью фигуры и плоскостью проекции.
— угол между плоскостью фигуры и плоскостью проекции.
6. Метод объемовпомогает найти расстояние от точки до плоскости. Надо выбрать треугольную пирамиду, записать ее объем двумя способами и найти из полученного уравнения нужное расстояние.
7. Сначала изучаем «классику». После этого, если время есть, можно браться и закоординатный метод
Почему именно в таком порядке?
Конечно, координатный метод удобен. Однако большинство задач по стереометрии из вариантов ЕГЭ «заточены» под классику.
И если в решении задачи координатным методом вы сделаете арифметическую ошибку — можете потерять все баллы. Эксперт не будет разбираться, правильно ли вы посчитали определитель или смешанное произведение векторов. Потому что эти темы не входят в школьную программу, и составители «конструировали» задачи по стереометрии так, чтобы они решались обычными, «классическими» способами.
Задание 14
Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.
|
|
|
Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!
Темы для повторения:
New
Решаем задачи из сборника И. В. Ященко, 2021
Квадратичные неравенства
Метод интервалов
Уравнения и неравенства с модулем
Иррациональные неравенства
Показательные неравенства
Логарифмические неравенства
Метод замены множителя (рационализации)
Решение неравенств: основные ошибки и полезные лайфхаки
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15
Логарифмические неравенства повышенной сложности
Разберем неравенства разных типов из вариантов ЕГЭ по математике.
Дробно-рациональные неравенства
1. Решите неравенство:

Сделаем замену 
Тогда 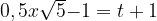 , а
, а 
Получим:
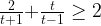
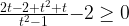



Решим неравенство относительно t методом интервалов:

Получим:

Вернемся к переменной x: 

Ответ: 
Показательные неравенства
2. Решите неравенство 
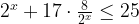
Сделаем замену  Получим:
Получим:
 Умножим неравенство на
Умножим неравенство на 
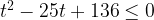
Дискриминант квадратного уравнения 
 Значит, корни этого уравнения:
Значит, корни этого уравнения: 
Разложим квадратный трехчлен  на множители.
на множители.


 . Вернемся к переменной x.
. Вернемся к переменной x.
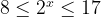
Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

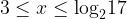
Ответ: 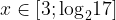
Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ,
3. Решите неравенство 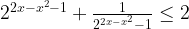
Сделаем замену  Получим:
Получим:
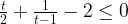
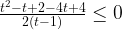




Вернемся к переменной 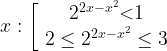
Первое неравенство решим легко: 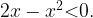 С неравенством
С неравенством  тоже все просто. Но что делать с неравенством
тоже все просто. Но что делать с неравенством 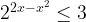 ? Ведь
? Ведь  Представляете, как трудно будет выразить х?
Представляете, как трудно будет выразить х?
|
|
|
Оценим 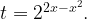 Для этого рассмотрим функцию
Для этого рассмотрим функцию 
Сначала оценим показатель степени. Пусть  Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом
Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом 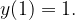
Мы получили, что 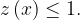
Тогда  , и это значит, что
, и это значит, что  Значение
Значение  не достигается ни при каких х.
не достигается ни при каких х.
Но если  и
и 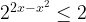 , то
, то 
Мы получили:

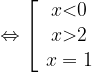
Ответ: 
|
|
|


