 |
Квадратичная функция. Необходимая теория
|
|
|
|
Квадратичная функция. Необходимая теория
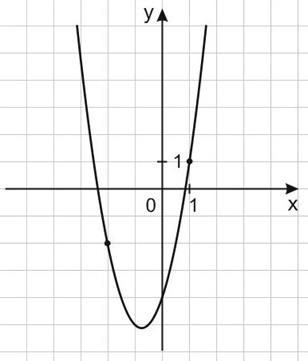
4. На рисунке изображен график функции 
Найдите b.
Решение:
На рисунке — квадратичная парабола 
полученная из графика функции 
сдвигом на 1 вправо, то есть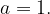 
Получим: 
Ответ: -2.
5. На рисунке изображен график функции 
. Найдите с.
Решение:
На рисунке изображена парабола, ветви которой направлены вверх, значит, коэффициент при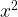 
положительный. График сдвинут относительно графика функции на 1 единицу вправо вдоль оси Ох. Формула функции имеет вид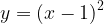 
.
Значит, с = 1.
Ответ: 1
6. На рисунке изображён график функции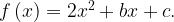 
Найдите 
Решение:
График функции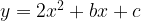 
проходит через точки с координатами (1; 1) и (-2; -2). Подставляя координаты этих точек в формулу функции, получим:
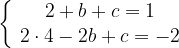
отсюда 
Формула функции имеет вид:
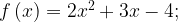
Ответ: 31.
7. На рисунке изображены графики функций 
и 
которые пересекаются в точках А и В. Найдите абсциссу точки В.
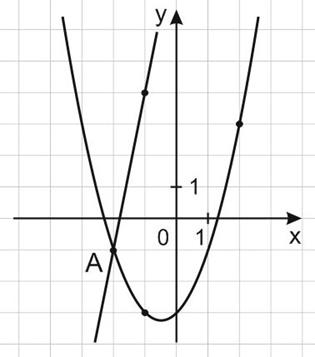
Решение:
Найдем a, b и c в формуле функции 
. График этой функции пересекает ось ординат в точке (0; -3), поэтому 
График функции 
проходит через точки (-1; -3) и (2; 3). Подставим по очереди координаты этих точек в формулу функции:
отсюда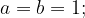 
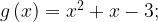
Найдем абсциссу точки B. Для точек A и B: 
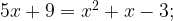
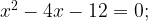
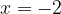(это абсцисса точки A) или 
(это абсцисса точки B).
Ответ: 6.
Степенные функции. Необходимая теория
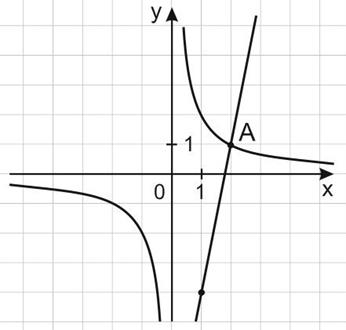
8. На рисунке изображены графики функций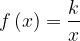 
и 
, которые пересекаются в точках А и В. Найдите абсциссу точки В.
Решение:
График функции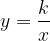 
проходит через точку (2; 1); значит,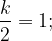 
График функции проходит через точки (2; 1) и (1; -4),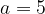 
— угловой коэффициент прямой; (находим как тангенс угла наклона прямой и положительному направлению оси X); тогда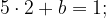 
Для точек A и B имеем: 
Отсюда 
(абсцисса точки A) или 
(абсцисса точки B).
|
|
|
Ответ: -0, 2.
9. На рисунке изображён график функции 
. Найдите f (6, 76).
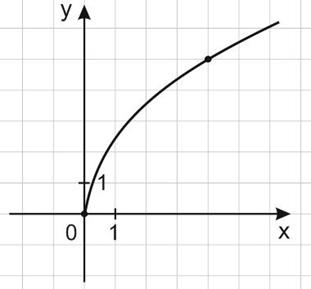
Решение:
Функция задана формулой:
Ее график проходит через точку (4; 5); значит, 
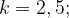
Тогда 
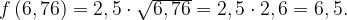
Ответ: 6, 5.
10. На рисунке изображен график функции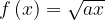 
. Найдите 
.
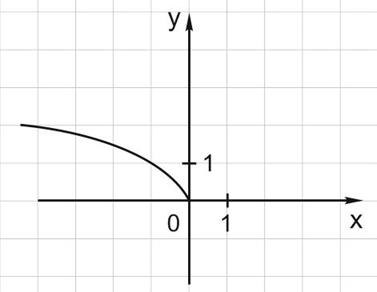
Решение:
График функции на рисунке симметричен графику функции 
относительно оси Y. Он проходит через точку (-1; 1). Значит, формула изображенной на рисунке функции: 
, а = - 1. Тогда 
=5.
Ответ: 5
Показательная функция. Необходимая теория
11. На рисунке изображён график функции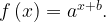 
Найдите 
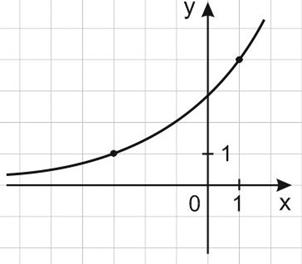
Решение:
График функции проходит через точки (-3; 1) и (1; 4). Подставив по очереди координаты этих точек в формулу функции 
получим:
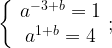
Поделим второе уравнение на первое:
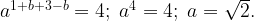
Подставим во второе уравнение:
Ответ: 0, 25.
12. На рисунке изображен график функции 
. Найдите 
Решение:
График функции проходит через точку 
Это значит, что 
формула функции имеет вид: 
.
Ответ: 2
Логарифмическая функция. Необходимая теория
13. На рисунке изображён график функции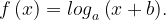 
Найдите 
Решение:
График функции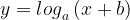 
проходит через точки (-3; 1) и (-1; 2). Подставим по очереди эти точки в формулу функции.
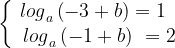
Отсюда: 
Вычтем из второго уравнения первое:
или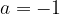 
— не подходит, так как 
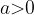(как основание логарифма).
Тогда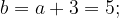 
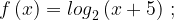
Ответ: 4.
14. На рисунке изображен график функции 
.
Найдите f(0, 2).
Решение:
График логарифмической функции на рисунке проходит через точки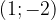 
и 
. Подставив по очереди координаты этих точек в формулу функции, получим систему уравнений:
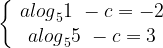
Формула функции: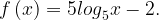 
Найдем 
:
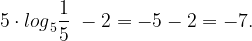
Ответ: -7.
Тригонометрические функции. Необходимая теория
15. На рисунке изображён график функции 
Найдите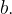 
Решение:
График функции 
сдвинут на 1, 5 вверх; 
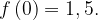Значит, 
Амплитуда (наибольшее отклонение от среднего значения).
Это график функции 
Он получен из графика функции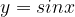 
растяжением в 2 раза по вертикали и сдвигом вверх на 
.
|
|
|
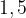Ответ:
16. На рисунке изображён график функции
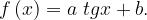
Найдите 
.
Решение:
На рисунке — график функции 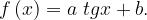Так как 
График функции проходит через точку A 
Подставим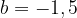 
и координаты точки А в формулу функции.
Так как 
получим: 
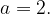
Ответ: 2.
17. На рисунке изображен график периодической функции у = f(x). Найдите значение выражения 
Решение:
Функция, график которой изображен на рисунке, не только периодическая, но и нечетная, и если 
то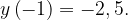 
Пользуясь периодичностью функции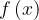 
, период которой T = 4, получим:
Ответ: 5
Задание10
В 2022 году в варианты ЕГЭ по математике добавились новые задачи по теории вероятностей. По сравнению с теми, которые раньше были в варианте, это повышенный уровень сложности.
Мы разберем задачу №10 из Демоверсии ЕГЭ-2022, задания из Методических рекомендаций ФИПИ для учителей и аналогичные им.
1. Демо-версия ЕГЭ-2022
Симметричную игральную кость бросили 3 раза. Известно, что в сумме выпало
6 очков. Какова вероятность события «хотя бы раз выпало 3 очка»?
Решение:
Выпишем возможные исходы как тройки чисел так, чтобы в сумме получилось 6.
Всего 10 возможных исходов. Благоприятные исходы помечены красным цветом, их 6.
По определению вероятности получаем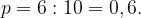 
2. Игральный кубик бросают дважды. Известно, что в сумме выпало 8 очков. Найдите вероятность того, что во второй раз выпало 3 очка.
Решение:
Выпишем возможные варианты получения 8 очков в сумме:
Подходит только вариант 5; 3. Вероятность этого события равна 1: 5 = 0, 2 (один случай из 5 возможных).
Ответ: 0, 2
3. В ящике 4 красных и 2 синих фломастера. Фломастеры вытаскивают по очереди в случайном порядке. Какова вероятность того, что первый раз синий фломастер появится третьим по счету?
Решение:
Благоприятными будут следующие исходы:
Первый раз – вытащили красный фломастер,
И второй раз – красный,
А третий раз – синий.
Вероятность вытащить красный фломастер (которых в ящике 4) равна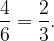 
После этого в ящике остается 5 фломастеров, из них 3 красных, вероятность вытащить красный равна 
Наконец, когда осталось 4 фломастера и из них 2 синих, вероятность вытащить синий равна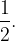 
Вероятность события {красный – красный – синий } равна произведению этих вероятностей, то есть
Ответ: 0, 2
|
|
|
4. В коробке 10 синих, 9 красных и 6 зеленых фломастеров. Случайным образом выбирают 2 фломастера. Какова вероятность того, что окажутся выбраны один синий и один красный фломастер?
Решение:
Всего в коробке 25 фломастеров.
В условии не сказано, какой из фломастеров вытащили первым – красный или синий.
Предположим, что первым вытащили красный фломастер. Вероятность этого 
в коробке остается 24 фломастера, и вероятность вытащить вторым синий равна 
Вероятность того, что первым вытащили красный, а вторым синий, равна 
А если первым вытащили синий фломастер? Вероятность этого события равна 
Вероятность после этого вытащить красный равна 
вероятность того, что синий и красный вытащили один за другим, равна 
Значит, вероятность вытащить первым красный, вторым синий или первым синий, вторым красный равна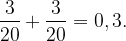 
А если их доставали из коробки не один за другим, а одновременно? Вероятность остается такой же: 0, 3. Потому что она не зависит от того, вытащили мы фломастеры один за другим, или с интервалом в 2 секунды, или с интервалом в 0, 5 секунды… или одновременно!
Ответ: 0, 3.
5. При подозрение на наличие некоторого заболевания пациента отправляют на ПЦР-тест. Если заболевание действительно есть, то тест подтверждает его в 86 % случаев. Если заболевания нет, то тест выявляет отсутствие заболевания в среднем в 94% случаев.
Известно, что в среднем тест оказывается положительным у 10% пациентов, направленных на тестирование. При обследовании некоторого пациента врач направил его на ПЦР-тест, который оказался положительным. Какова вероятность того, что пациент действительно имеет это заболевание?
Решение:
Уточним условие: " Какова вероятность того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание? ". В такой формулировке множество возможных исходов - это число пациентов с положительным результатом ПЦР-теста, причем только часть из них действительно заболевшие.
Пациент приходит к врачу и делает ПЦР-тест. Он может быть болен этим заболеванием – с вероятностью х. Тогда с вероятностью 1 – х он этим заболеванием не болен.
|
|
|
Анализ пациента может быть положительным по двум причинам:
а) пациент болеет заболеванием, которое нельзя называть, его анализ верен; событие А,
б) пациент не болен этим заболеванием, его анализ ложно-положительный, событие В.
Это несовместные события, и вероятность их суммы равна сумме вероятностей этих событий.
Имеем:
Мы составили уравнение, решив которое, найдем вероятность x.
Что такое вероятность х? Это вероятность того, что пациент, пришедший к доктору, действительно болен. Здесь множество возможных исходов - это количество всех пациентов, пришедших к доктору.
Нам же нужно найти вероятность z того, что пациент, ПЦР-тест которого положителен, действительно имеет это заболевание. Вероятность этого события равна 
(пациент болен и ПЦР-тест выявил заболевание, произведение событий). С другой стороны, эта вероятность равна 
(у пациента положительный результат ПЦР-теста, и при выполнении этого условия он действительно болен).
Получим: 
отсюда 
Ответ: 0, 43
Вероятность того, что пациент с положительным результатом ПЦР-теста действительно болен, меньше половины!
Кстати, это реальная проблема для диагностики в медицине, то есть в задаче отражена вполне жизненная ситуация.
6. Телефон передает sms-сообщение. В случае неудачи телефон делает следующую попытку. Вероятность того, что сообщение удастся передать без ошибок в каждой следующей попытке, равна 0, 4. Найдите вероятность того, что для передачи сообщения потребуется не больше 2 попыток.
Решение:
Здесь все просто. Либо сообщение удалось передать с первой попытки, либо со второй.
Вероятность того, что сообщение удалось передать с первой попытки, равна 0, 4.
С вероятностью 0, 6 с первой попытки передать не получилось. Если при этом получилось со второй, то вероятность этого события равна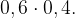 
Значит, вероятность того, что для передачи сообщения потребовалось не более 2 попыток, равна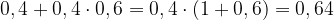 
Ответ: 0, 64
7. Симметричную монету бросают 10 раз. Во сколько раз вероятность события «выпадет ровно 5 орлов» больше вероятности события «выпадет ровно 4 орла»?
Решение:
А это более сложная задача. Можно, как и в предыдущих, пользоваться определением вероятности и понятиями суммы и произведения событий. А можно применить формулу Бернулли.
Формула Бернулли:
– Вероятность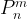 
того, что в n независимых испытаниях некоторое случайное событие A наступит ровно m раз, равна:
где
p – вероятность появления события A в каждом испытании;
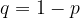– вероятность появления события A в каждом испытании
Коэффициент 
часто называют биномиальным коэффициентом.
|
|
|
О том, что это такое, расскажем с следующих статьях на нашем сайте. Чтобы не пропустить – подписывайтесь на нашу рассылку.
А пока скажем просто, как их вычислять.
Нет, это не заклинание. Не нужно громко кричать: Эн!!!! Поделить на эм! И на эн минус эм! То, что вы видите в формуле, – это не восклицательные знаки. Это факториалы. На самом деле все просто: n! (читается: эн факториал) – это произведение натуральных чисел от 1 до n. Например,
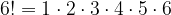
Пусть вероятность выпадения орла при одном броске монеты равна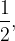 
вероятность решки тоже 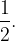Давайте посчитаем вероятность того, что из 10 бросков монеты выпадет ровно 5 орлов.
Вероятность выпадения ровно 4 орлов равна
Найдем, во сколько раз 
больше, чем 
Ответ: 1, 2
8. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым отдельным выстрелом равна 0, 6. Во сколько раз вероятность события «стрелок поразит ровно 5 мишеней» больше вероятности события «стрелок поразит ровно 4 мишени»?
Решение:
Стрелок поражает мишень с первого или со второго выстрела;
Вероятность поразить мишень равна
Вероятность поразить 5 мишеней из 5 равна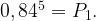 
Вероятность поразить 4 мишени из 5 находим по формуле Бернулли:
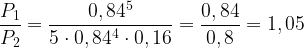
9. Стрелок стреляет по пяти одинаковым мишеням. На каждую мишень дается не более двух выстрелов, и известно, что вероятность поразить мишень каждым выстрелом равна 0, 5. Во сколько раз вероятность события «стрелок поразит ровно 3 мишени» больше вероятности события «стрелок поразит ровно 2 мишени»?
Решение:
Найдем вероятность поразить одну мишень – с первого или со второго выстрела.
С вероятностью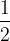 
стрелок поражает мишень первым выстрелом (и больше по ней не стреляет).
Найдем вероятность того, что стрелок поразит мишень вторым выстрелом. Она равна 
так как с вероятностью 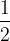он промахнулся в первый раз и с вероятностью 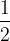второй выстрел был удачным.
Значит, вероятность поразить одну мишень первым или вторым выстрелом равна 
Теперь нам на помощь придет формула Бернулли.
Найдем вероятность того, что стрелок поразит ровно 3 мишени из 5.
Вероятность поразить ровно 2 мишени из пяти
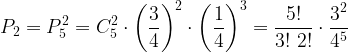
Заметим, что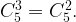 
Получим:
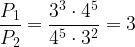
Ответ: 3.
10. Стрелок в тире стреляет по мишени. Известно, что он попадает в цель с вероятностью 0, 3 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать этому стрелку, чтобы вероятность поражения цели была не менее 0, 6?
Решение:
Похожие задачи были в Банке заданий ФИПИ и раньше. Пусть у стрелка есть n патронов. Стрелок может поразить цель первым, вторым … n-ным выстрелом, и все эти исходы для нас благоприятны. Не подходит только один исход – когда стрелок n раз стрелял и каждый раз был промах.
Вероятность промаха при одном выстреле равна 1 – 0, 3 = 0, 7.
Вероятность n промахов (из n выстрелов) равна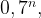 
а вероятность попасть с первого раза или сто второго... или с n-ого выстрела равна 
По условию, 
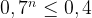
Если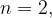 
то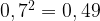 
– не подходит;
Для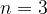 
условие выполнено,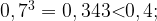 
Хватит 3 патронов.
Ответ: 3.
11. Игральную кость бросают до тех пор, пока сумма всех выпавших очков не превысит число 3. Какова вероятность того, что для этого потребуется ровно 3 броска? Ответ округлите до сотых.
Решение:
Кажется, что задача сложная (на самом деле нет).
Давайте подумаем: как получилось, что ровно за 3 броска игральной кости сумма выпавших очков оказалась больше трех? Из этого следует, что за 2 броска сумма выпавших очков была меньше 3 или равна 3.
Если за 2 броска сумма выпавших очков была меньше 3, значит, она была равна 2, то есть первый раз выпала единица и второй раз тоже единица. Вероятность этого события равна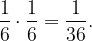 
Сколько же очков в этом случае должен дать третий бросок? Очевидно, что подойдет 2, 3, 4, 5, 6 – все, кроме 1. Вероятность того, что при третьем броске выпадет число очков, не равное единице, равна 
Значит, вероятность того, что при первых двух бросках выпали единицы, а при третьем – не единица, равна 
Нам подойдет также случай, когда сумма очков за первые 2 броска равна 3. Это значит, что выпали 2 и 1 или 1 и 2, то есть 2 благоприятных исхода из 36 возможных. Вероятность этого события равна 
При этом нам все равно, что выпадет при третьем броске: очевидно, что сумма очков при трех бросках будет больше трех.
Окончательно получаем: 
Ответ: 0, 08
Вот еще одна задача из Демо-версии ЕГЭ-2022:
12. В городе 48% взрослого населения – мужчины. Пенсионеры составляют 12, 6% взрослого населения, причём доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».
Решение:
Пусть N – численность взрослого населения в городе (мужчин и женщин).
Количество взрослых мужчин в городе: 0, 48N
Количество женщин в городе: 0, 52N
Из них 0, 15 * 0, 52N = 0, 078N женщин-пенсионеров,
Всего пенсионеров 0, 126N,
Тогда количество мужчин-пенсионеров равно 0, 126N – 0, 078N = 0, 048N.
Вероятность для случайно выбранного мужчины оказаться пенсионером равна отношению числа мужчин-пенсионеров к числу мужчин в городе, то есть 0, 048 N: 0, 48N = 0, 1.
Ответ. 0, 1.
Мы разобрали все доступные типы заданий №10 из вариантов ЕГЭ-2022. Раздел будет дополняться решениями новых задач– как только они появятся в Банке заданий ФИПИ.
Задание 11
Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.
Вот какие типы задач могут встретиться в этом задании:
Нахождение точек максимума и минимума функций
Исследование сложных функций
Нахождение наибольших и наименьших значений функций на отрезке
|
|
|
