 |
Примеры решения задач. Тема 3: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов». Краткая теория
|
|
|
|
Примеры решения задач.
Задача 1. Какая доля энергии фотона израсходована на работу вырывания фотоэлектрона, если красная граница фотоэффекта l0 = 307 нм, а максимальная кинетическая энергия 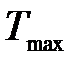 фотоэлектрона равна 1 эВ?
фотоэлектрона равна 1 эВ?
Дано:
l0 = 307 нм
 1 эВ
h = 6, 63·10-34 Дж·с
с = 3·108 м/с 1 эВ
h = 6, 63·10-34 Дж·с
с = 3·108 м/с
| СИ: 307·10-9 м 1, 6·10-19 Дж |
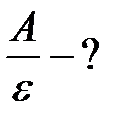
|
Решение:
Уравнение Эйнштейна для фотоэффекта – энергия кванта света e расходуется на работу выхода А электрона из вещества и на сообщение кинетической энергии Tmax (скорости) электрону:
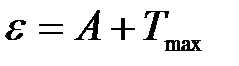 .
.
Работа выхода: 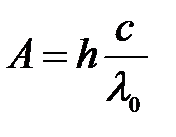 ,
,
где h – постоянная Планка; с – скорость света в вакууме.
Тогда отношение работы выхода к энергии фотона:
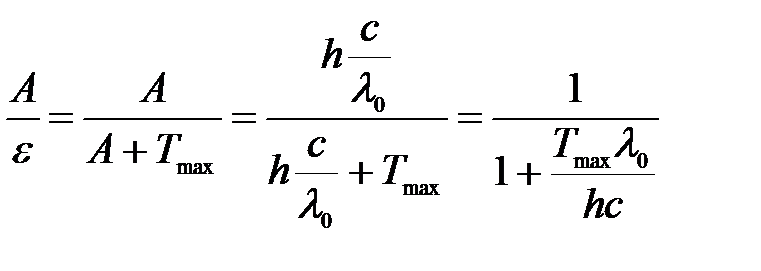 .
.
Вычислим:
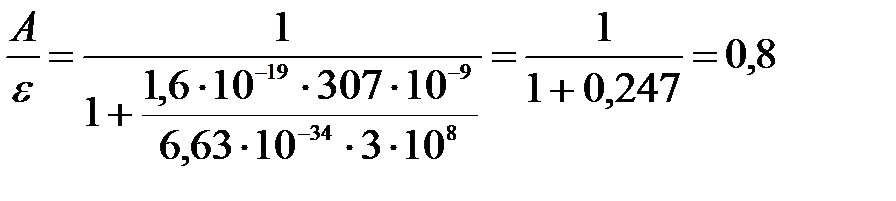 .
.
Ответ: 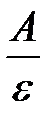 = 0, 8.
= 0, 8.
Задача 2. Для прекращения фотоэффекта, вызванного облучением ультрафиолетовым светом платиновой пластинки, нужно приложить задерживающую разность потенциалов 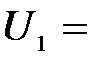 3, 7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
3, 7 В; если платиновую пластинку заменить другой пластинкой, то задерживающую разность потенциалов придётся увеличить до 6 В. Определить работу А выхода электронов с поверхности этой пластинки.
| Дано: U1 = 3, 7 В U2 = 6 В А1 = 6, 3 эВ | СИ: 10, 08× 10-19 Дж |
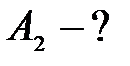
|
Решение:
Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света (e=h·v) расходуется на работу выхода электрона из вещества А и на сообщение кинетической энергии Т электрону:
e = А + Т.
Кинетическая энергия Т «гасится» работой сил электрического поля Аэл:
Т = Аэл. Учтём, что Аэл = еU. Тогда:  .
.
Тогда для первой и второй пластинки:
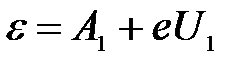 , ,
| |
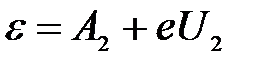 . .
|
Приравняем правые части уравнений:
 .
.
Выразим интересующую нас работу выхода для второй пластинки:
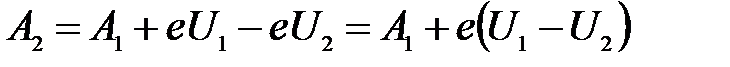 .
.
Подставим числа:
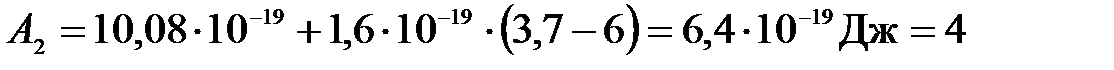 (эВ),
(эВ),
или сразу в электрон-вольтах:
|
|
|
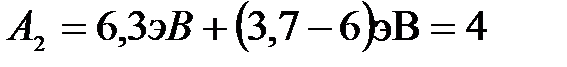 .
.
Ответ: А2 = 4 эВ.
Задача 3. “Красная граница” фотоэффекта для некоторого металла равна 500 нм. Определить: 1) работу выхода электронов из этого металла; 2) максимальную скорость электронов, вырываемых из этого металла светом, с длиной волны 400 нм.
| Дано: λ 0 = 500 нм λ = 400 нм h = 6, 63·10-34 Дж·с m = 9, 11·10-31 кг с = 3·108 м/с | СИ: 5× 10-7 м 4× 10-7 м |
| 1) Авых =? 2) υ max =? |
Решение:
1) Уравнение Эйнштейна для «красной границы» при фотоэффекте:
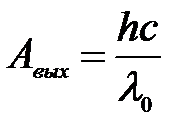 ,
,
где с – скорость света в вакууме, h – постоянная Планка.
Подставим числа:
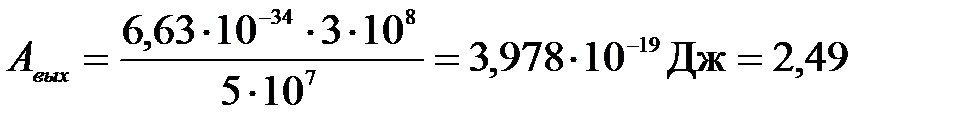 (эВ)
(эВ)
Следует напомнить, что 1 эВ = 1, 6·10-19 Дж.
2) Согласно уравнению Эйнштейна, при фотоэффекте энергия кванта света ε расходуется на работу выхода электрона Авых из металла и на сообщение кинетической энергии Т электрону:
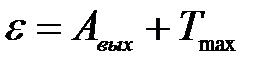 .
.
Энергия фотона: 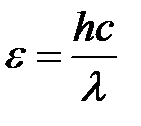 .
.
Кинетическая энергия: 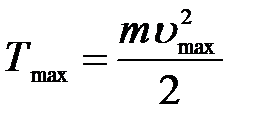 .
.
С учетом всех формул:
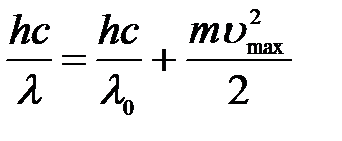 =>
=> 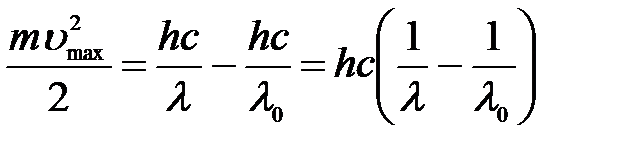 .
.
Откуда максимальная скорость электронов:
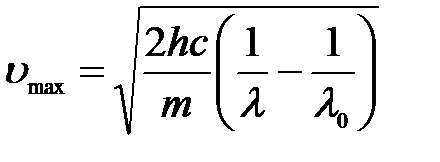 ,
,
где m – это масса электрона.
Подставим числа:
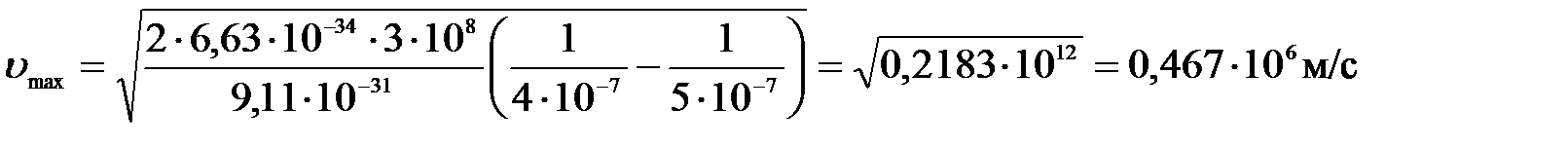 .
.
Ответ: 1) Авых = 2, 49 эВ; 2) υ max = 467 км/с.
Задача 4. Какая доля энергии фотона при эффекте Комптона приходится на электрон отдачи, если фотон претерпел рассеяние на угол 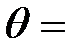 180°? Энергия (
180°? Энергия ( 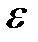 ) фотона до рассеяния равна 0, 255 МэВ.
) фотона до рассеяния равна 0, 255 МэВ.
Дано:
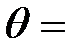 180° 180°
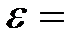 0, 255 МэВ
Е0 = 0, 511 МэВ 0, 255 МэВ
Е0 = 0, 511 МэВ
|

|
Решение:
Закон сохранения энергии:
e = 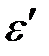 + Т,
+ Т,
где e – энергия падающего фотона, ε / – энергия рассеянного (отразившегося) фотона, Т – кинетическая энергия электрона.
Выразим кинетическую энергию электрона отдачи Т:
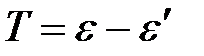 .
.
Тогда отношение кинетической энергии электрона отдачи к энергии падающего фотона:
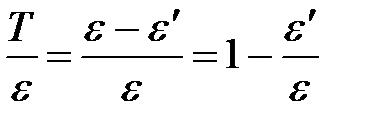 . .
|
Энергия рассеянного фотона: 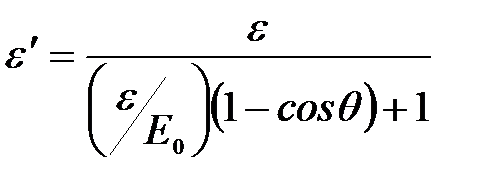 .
.
Откуда: 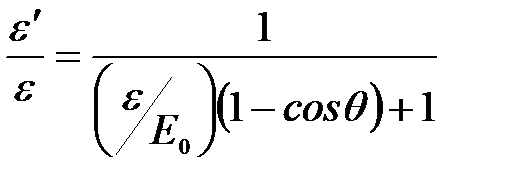 .
.
Следовательно,  .
.
Произведём вычисления: 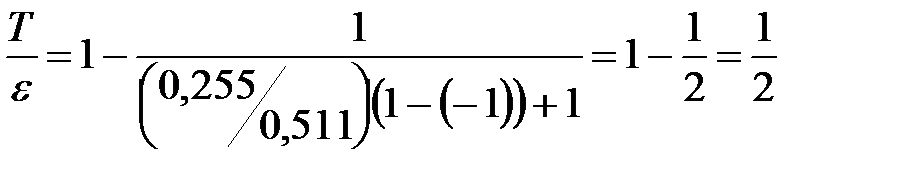 .
.
Ответ: 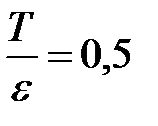 .
.
Тема 3: «Планетарная модель атома. Строение атома водорода по Бору. Спектры излучения атомов»
Краткая теория
В 19 веке впервые были открыты явления, обнаруживающие сложность строения и свойств атомов, которые до этого рассматривались как мельчайшие частицы вещества. Так в 1833 году М. Фарадей установил, что ток в растворе электролита – это упорядоченное движение заряженных частиц (ионов), минимальный заряд которых примерно равный е = 1, 60∙ 10-19 Кл был назван элементарным электрическим зарядом. В 1896 году французский ученый Беккерель обнаружил явление естественной радиоактивности солей урана. Это явление исследовали Пьер и Мария Кюри, доказав, что из атомов вылетают и электроны, и положительно заряженные частицы (впоследствии названные α -частицами). На сложную структуру атомов указывали спектроскопические исследования, которые привели к открытию линейчатых спектров атомов. В начале XIX века были открыты дискретные спектральные линии в излучении атомов водорода в видимой части спектра, и впоследствии были установлены математические закономерности, связывающие длины волн этих линий (И. Бальмер, 1885 г. ). В 1897 году Дж. Томсон открыл электрон и измерил отношение e/m заряда электрона к массе. Опыты Томсона подтвердили вывод о том, что электроны входят в состав атомов, причем носителями отрицательного заряда атомов являются легкие электроны, масса которых составляет лишь малую долю массы атомов. Основная часть массы атомов связана с положительным зарядом.
|
|
|
В первой модели атома Дж. Томсона (1903 г. ) атом рассматривался как заполненный положительным электричеством шар, внутри которого находились электроны. Атом в целом был электронейтрален. Однако в дальнейшем выяснилась несостоятельность этой модели.
В начале ХХ века английский физик Э. Резерфорд, анализируя данные по рассеянию  -частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
-частиц тонкими металлическими образцами, выдвинул так называемую «планетарную» модель строения атома.
Рассеяние α -частиц при прохождении через фольгу вызывается кулоновскими силами, т. е. электрическим взаимодействием частицы и заряда атома. Гравитационное взаимодействие в 1033 раз меньше, поэтому фактически роли не играет.
Какие же заряды в атоме вызывают рассеяние α -частиц? Электроны не могут этого сделать, так как их масса много меньше массы частицы: ma=7350me. При взаимодействии с электронами быстро движущаяся частица не изменяет направление своего движения.
|
|
|
|
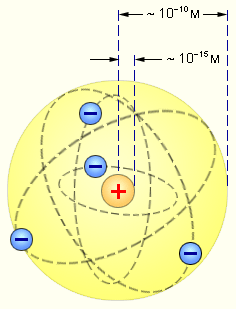
| Рис. 3. 1. Планетарная модель атома |
Причиной рассеяния a-частиц является их взаимодействие с положительно заряженными частицами атома, занимающими очень малую область атома. Резерфорд назвал эту область ядром. В ядре сосредоточена почти вся масса атома и весь положительный заряд. Обобщив результаты опытов, Резерфорд предложил следующую модель строения атома, в рамках которой предполагается, что в центре атома находится тяжелое положительно заряженное ядро, вокруг которого, подобно планетам вокруг Солнца, вращаются легкие отрицательно заряженные электроны. Атомы имеют размеры порядка 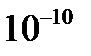 м, а ядра – порядка
м, а ядра – порядка 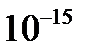 м, т. е. атом на 99. 9% пустой (рис. 3. 1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью:
м, т. е. атом на 99. 9% пустой (рис. 3. 1). Практически вся масса атома сосредоточена в ядре, поэтому ядерная материя обладает огромной плотностью: 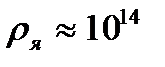 г/cм3.
г/cм3.
Однако планетарная модель атома является внутренне противоречивой. Движущийся с ускорением заряд излучает электромагнитную волну. При этом энергия атома уменьшается: электрон должен упасть на ядро, а атом прекратить свое существование.
На самом деле атомы химических элементов представляют собой устойчивые структуры, существующие десятки тысяч лет без изменения. Поэтому модель атома Резерфорда была дополнена рядом положений, автором которых является датский физик Бор.
В 1913 году Бор показал, что несовпадение с экспериментом выводов, основанных на модели Резерфорда, возникло потому, что поведение микрочастиц нельзя описывать теми же законами, что и макроскопических тел.
Бор предположил, что величины характеризующие микромир, должны квантоваться, т. е. они могут принимать только определенные дискретные значения.
Законы микромира - квантовые законы. Эти законы в начале 20 столетия еще не были установлены наукой. Бор сформулировал их в виде трех постулатов, дополняющих ( и " спасающих" ) атом Резерфорда.
Первый постулат ( постулат стационарных состояний ):
Атомы имеют ряд стационарных состояний соответствующих определенным значениям энергий: Е1, Е2... En. Находясь в стационарном состоянии, атом энергии не излучает и не поглощает энергию, несмотря на движение электронов. Энергии стационарных состояний образуют дискретный спектр.
|
|
|
Второй постулат ( правило квантования орбит):
В стационарном состоянии атома электроны движутся по стационарным орбитам, для которых выполняется квантовое соотношение:
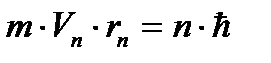 (3. 1)
(3. 1)
где m - масса электрона, rn- радиус орбиты с номером n (n=1, 2, 3... ), 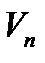 - скорость электрона на этой орбите, ħ - постоянная Планка.
- скорость электрона на этой орбите, ħ - постоянная Планка.
Третий постулат (правило частот):
Излучение или поглощение энергии атомом происходит при переходе его из одного стационарного состояния в другое. При этом излучается или поглощается порция энергии (квант), равная разности энергий стационарных состояний, между которыми происходит переход:
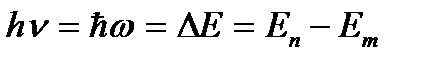 (3. 2)
(3. 2)
Постулаты Бора противоречат законам классической физики. Они выражают характерную особенность микромира - квантовый характер происходящих там явлений. Выводы, основанные на постулатах Бора, хорошо согласуются с экспериментом. Например, объясняют закономерности в спектре атома водорода, происхождение характеристических спектров рентгеновских лучей и т. д. На рис. 3. 2 показана часть энергетической диаграммы стационарных состояний атома водорода.
Планетарная модель продемонстрировала прекрасное согласие с экспериментом при описании атома водорода, однако для описания свойств многоэлектронных атомов она оказалась не пригодна. Основной недостаток этой модели заключается в отсутствии учета взаимодействия электронов между собой.
Постулаты Бора нашли своё экспериментальное подтверждение в опытах Д. Франка и Г. Герца (1913), в которых изучались столкновения электронов с атомами газов.
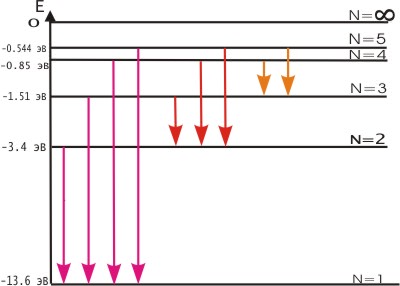
Рис. 3. 2. Энергетическая диаграмма стационарных состояний атома водорода
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем - систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга. 
Выражение для радиуса n-й стационарной орбиты:
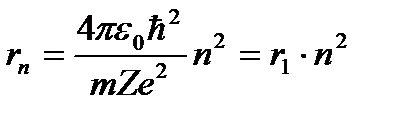 , (n = 1, 2, 3, …). (3. 3)
, (n = 1, 2, 3, …). (3. 3)
Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровским радиусом (rB), равен
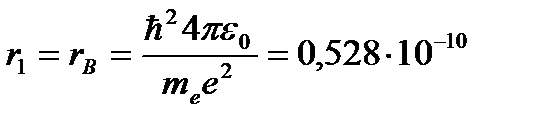 (3. 4)
(3. 4)
Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии  и потенциальной энергии в электростатическом поле ядра
и потенциальной энергии в электростатическом поле ядра 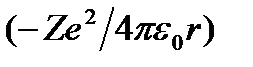 :
:
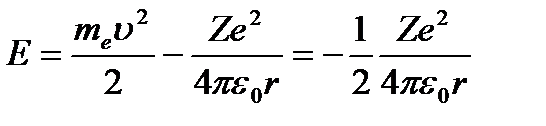 (3. 5)
(3. 5)
Учитывая квантованные для радиуса n-й стационарной орбиты значения (3. 4), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
|
|
|
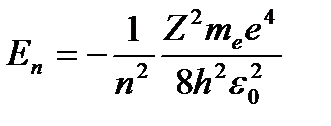 (n = 1, 2, 3, …), (3. 6)
(n = 1, 2, 3, …), (3. 6)
где m - масса электрона, e = 1. 610-19 Кл - и заряд электрона; 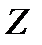 – порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
– порядковый номер элемента в таблице Менделеева. Знак « - » означает, что электрон находится в связанном состоянии.
Из формулы (3. 6) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (3. 6), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n = 1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
Придавая n различные целочисленные значения, получим для атома водорода (Z = 1) возможные уровни энергии, схематически представленные на рис. 3. 2 и 3. 3. На рис. 3. 2 изображена диаграмма энергетических уровней атома водорода и указаны переходы, соответствующие различным спектральным сериям. Рис. 3. 3 иллюстрирует образование спектральных серий в излучении атома водорода при переходе электрона с высоких стационарных орбит на более низкие.
Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = ∞. Атом водорода обладает, таким образом, минимальной энергией (Е1=-13, 6 эВ) при п = 1 и максимальной (Е∞ = 0) при n = ∞ . Следовательно, значение Е∞ = 0 соответствует ионизации атома (отрыву от него электрона). Согласно третьму постулату Бора, при переходе атома водорода (Z = 1) из стационарного состояния n в стационарное состояние т с меньшей энергией испускается квант
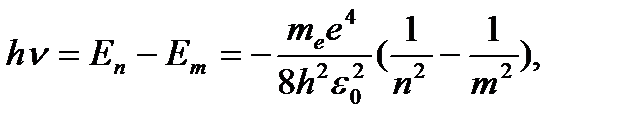 (3. 7)
(3. 7)
Откуда частота излучения
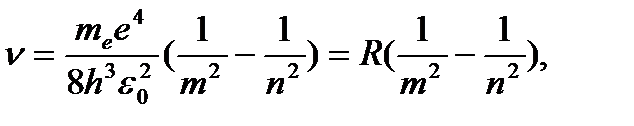 (3. 8)
(3. 8)
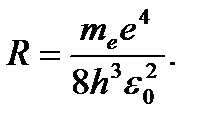 (3. 9)
(3. 9)
R – постоянная Ридберга.
Прекрасное согласие боровской теории атома водорода с экспериментом служило веским аргументом в пользу ее справедливости. Стало ясно, что атомы – это квантовые системы. Энергетические уровни стационарных состояний атомов дискретны.
Однако попытки применить теорию Бора к более сложным атомам (даже для атома гелия) не увенчались успехом. Эта теория обладает внутренними противоречиями: с одной стороны, применяет законы классической физики, а с другой - основывается на квантовых постулатах. Бор не смог дать физическую интерпретацию правилу квантования. Это было сделано де Бройлем (1923) на основе представлений о волновых свойствах частиц.
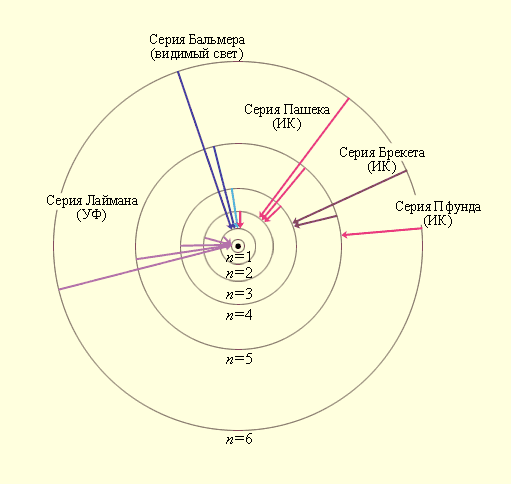
Рис. 3. 3. Стационарные орбиты атома водорода и образование
спектральных серий.
|
|
|


