 |
Примеры решения задач
|
|
|
|
Задача 1. Определить потенциальную П, кинетическую Т и полную Е энергии электрона, находящегося на первой орбите атома водорода (основное состояние).
| Дано: Z = 1 n = 1 mе = 9, 11·10-31 кг е = 1, 6·10-19 Кл h = 6, 626·10-34 Дж·с ε 0 = 8, 85·10-12 Ф/м |
| 1) П =? 2) Т =? 3) Е =? |
Решение:
Потенциальная энергия электрона в электростатическом поле ядра и радиус орбиты rn электрона:
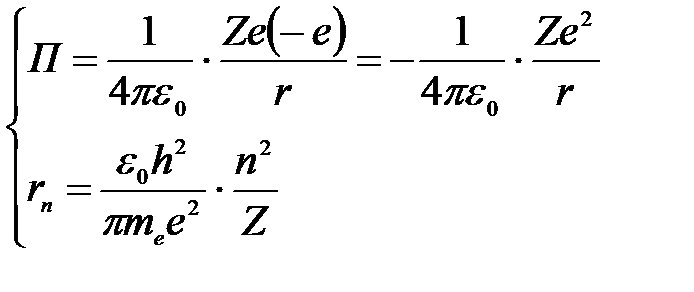 .
.
Тогда потенциальная энергия электрона на любой орбите водородоподобного атома (считаем энергию электрона в бесконечности равной нулю):
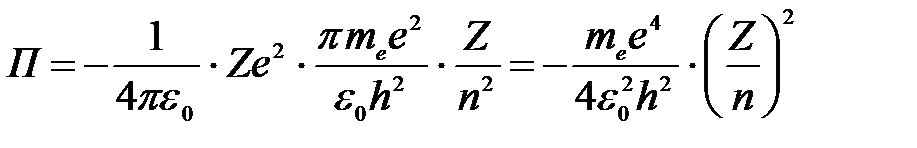 . .
|
Потенциальная энергия для основного состояния атома водорода Z = 1, n = 1:
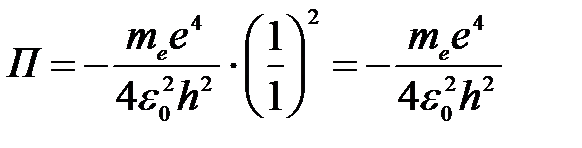 .
.
Вычислим:
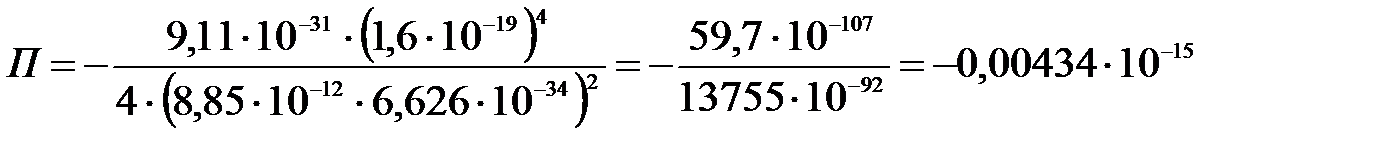 ;
;
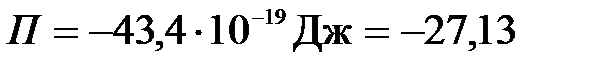 эВ.
эВ.
2) Кинетическая энергия электрона при движении по окружности и скорость электрона на этой орбите:
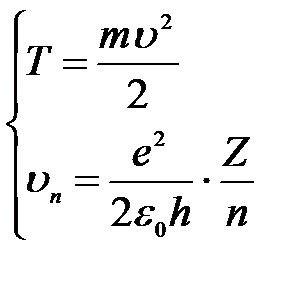 .
.
Тогда кинетическая энергия электрона на любой орбите водородоподобного атома:
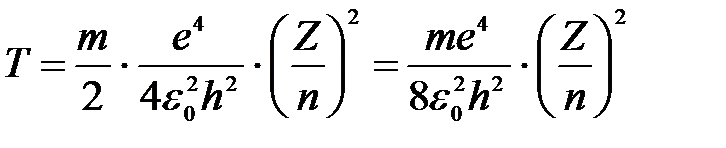 . .
|
Кинетическая энергия для основного состояния атома водорода Z=1, n=1:
 .
.
Вычислим:
 эВ.
эВ.
3) Полная энергия электрона на любой орбите водородоподобного атома:
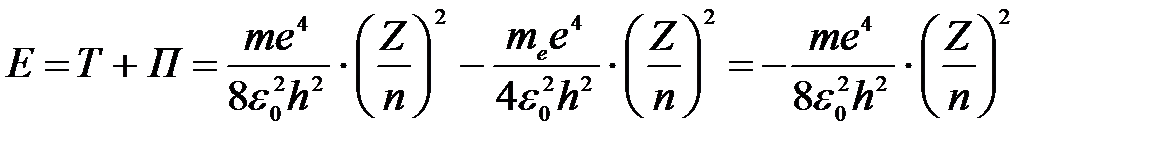 . .
| (3) |
Полная энергия для основного состояния атома водорода Z = 1, n = 1:
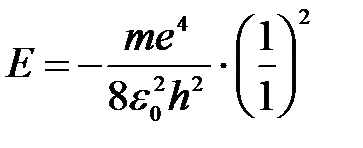 .
.
Вычислим:
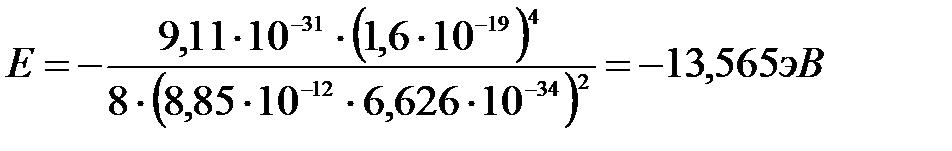 .
.
Задача 2. Определить энергию фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на второй.
| Дано: Z = 1 m = 2 n = 3 h=6, 626·10-34 Дж·с с = 3·108 м/с R = 3, 29 1015 c-1 R/ = 1, 097 107 м-1 Еi = 13, 6 эВ mе = 9, 11·10-31 кг е = 1, 6·10-19 Кл |
| ε 3, 2 =? |
Решение:
Способ 1. Энергия фотона:
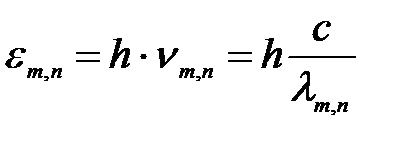 , (1)
, (1)
где h – постоянная Планка, с – скорость света в вакууме, ν – частота излучения, λ – длина волны излучения m, n – стационарные орбиты; m = 1, 2, 3, 4, 5, 6 (определяет серию), n = m + 1, m + 2, m + 3…(определяет отдельные линии этой серии), n = ∞ определяет границу серии.
|
|
|
Обобщённая формула Бальмера (сериальная формула):
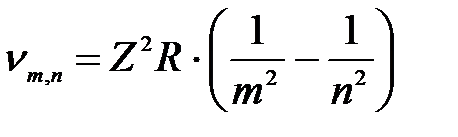 (2)
(2)
или 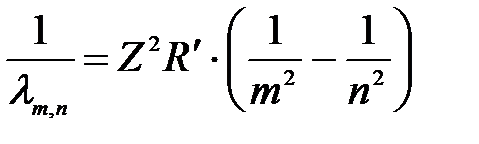 , (2-а) , (2-а)
|
где R = R/с = 3, 28805∙ 1015 1/с – постоянная Ридберга,
R/ = 1, 097373177∙ 107 м-1 – штриховая постоянная Ридберга,
Z – зарядовое число (порядковый номер в таблице Менделеева).
Подставим формулу (2) частоты в (1):
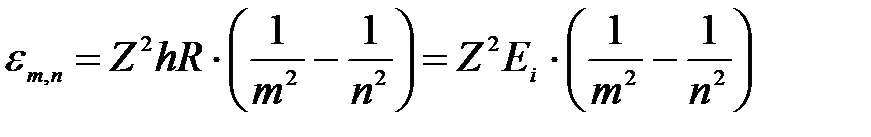 , ,
| (3а) |
или через длину волны:
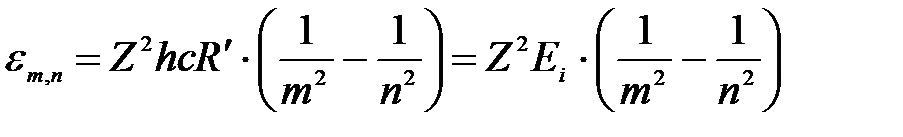 , ,
| (3б) |
где Еi – энергия ионизации водорода. Получили одинаковую формулу.
Произведем вычисления во внесистемных единицах:
 (эВ).
(эВ).
Способ 2. Второй постулат Бора (правило частот):
| ε n, m = Δ Е = Еn – Em = Eдо – Eпосле, | (4) |
где ε n, m – энергия испускаемого (поглощаемого) атомом фотона при переходе атома из одного стационарного состояния в другое; Еn и Em – энергии стационарных состояний, характеризуемые квантовыми числами n и m, определяемые по формуле:
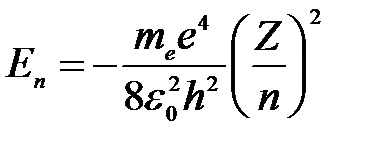 , ,
| (5) |
где е – элементарный заряд, ε 0 – электрическая постоянная, Z – атомный номер (зарядовое число, порядковый номер атома в таблице Д. И. Менделеева).
При Em < En происходит излучение фотона, при Em > En – его поглощение.
Тогда энергия испускаемого фотона:
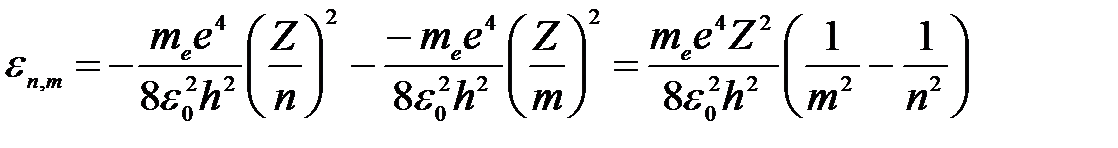 .
.
Подставим числа:
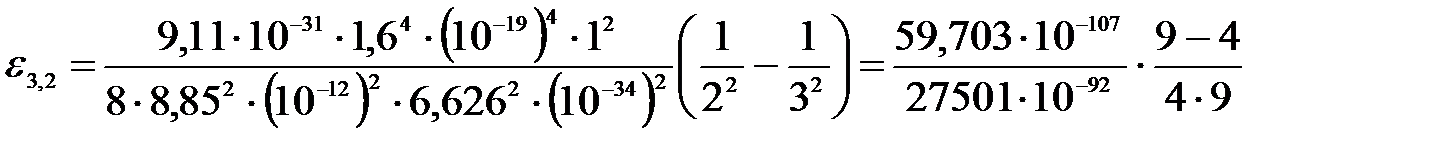 ;
;
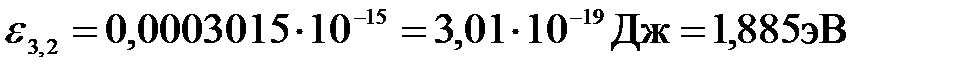 .
.
Ответ: ε 3, 2 = 1, 89 эВ, относится к серии Бальмера.
| орбита |
| e |
| Рис. 4. 4 |
Задача 3. Определить длину волны спектральной линии, соответствующую переходу электрона в атоме водорода с шестой боровской орбиты на вторую (рис. 3. 4) К какой серии относится эта линия? Которая она по счёту?
Дано:
m = 2
n = 6
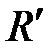 = 1, 097 107 м-1 = 1, 097 107 м-1
|
| l =? |
Решение:
Запишем обобщенную формулу Бальмера:
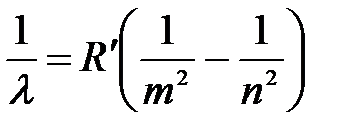 ,
,
где l – длина волны спектральных линий в спектре атома Бора; m – определяет серию; n – определяет отдельные линии этой серии (m < n); 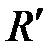 – штриховая постоянная Ридберга.
– штриховая постоянная Ридберга.
Отсюда длина волны:
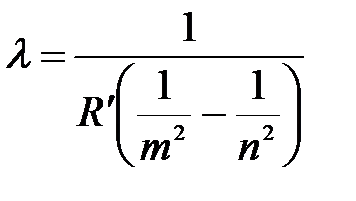 .
.
Произведем вычисления:
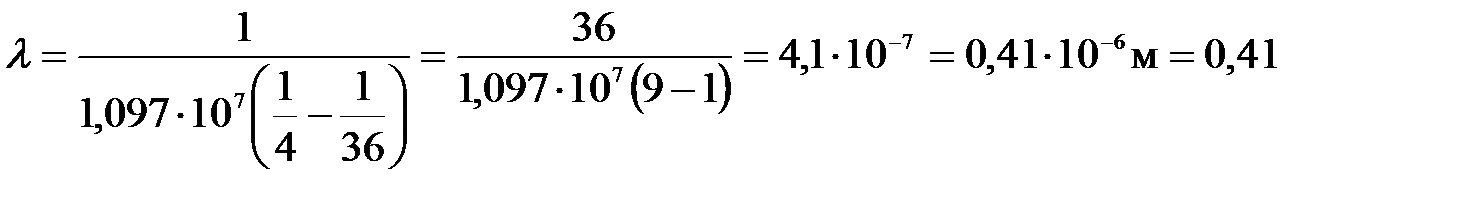 мкм.
мкм.
Это – серия Бальмера, т. к. m = 2. По счёту она 4я, т. к. n – m = 6 – 2 =4.
Ответ: l = 0, 41 мкм, серия Бальмера, по счёту № 4.
|
|
|
Задача 4. Насколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны l = 486 нм?
| Дано: Z = 1 l = 486 нм | СИ: 486∙ 10-9 м |
| DЕк -? |
Решение:
Из закона сохранения энергии: разность полных энергий электрона соответствующих орбит равна энергии излучения:
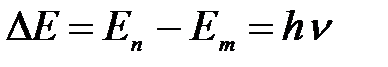 .
.
Частота это есть отношение скорости света к длине волны:
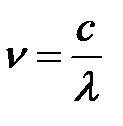 .
.
Полная энергия электрона по модулю равна кинетической энергии:
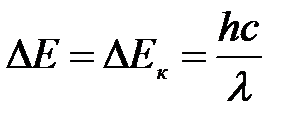 .
.
Подставим численные значения:
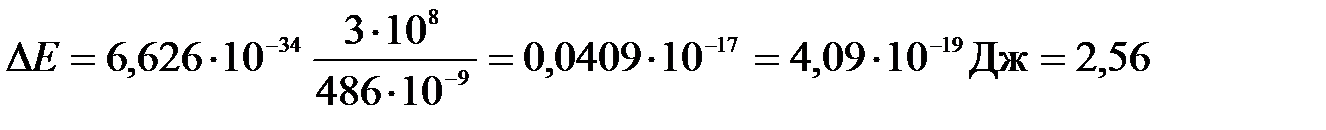 (эВ).
(эВ).
Ответ: DЕк = 2, 56 эВ.
|
|
|


