 |
Введение. 1. Арифметические основы ЭВМ. 1. 1. Основные форматы чисел. 1. 2. Машинные коды алгебраических чисел
|
|
|
|
МОСКОВСКИЙ АВТОМОБИЛЬНО-ДОРОЖНЫЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
(МАДИ)
Т. М. АЛЕКСАНДРИДИ, Б. Н. МАТЮХИН, Е. Н. МАТЮХИНА
ОРГАНИЗАЦИЯ ЭВМ И СИСТЕМ
Учебное пособие
Рекомендовано Учебно-методическим объединением вузов по университетскому политехническому образованию в качестве учебного пособия для направления 552800 «Информатика и вычислительная техника» и направления 654600 «Информатика и вычислительная техника» по специальности 230102 «Автоматизированные системы обработки информации и управления (АС) ».
МОСКВА 2010
Введение
Настоящее учебное пособие предназначено для студентов направления 552800 «Информатика и вычислительная техника» и направления 654600 «Информатика и вычислительная техника» по специальности 230102 «Автоматизированные системы обработки информации и управления (АСОИУ)» и используется при изучении теоретических разделов дисциплин «Схемотехника» и «Организация ЭВМ и систем», выполнении лабораторных работ, а также при курсовом и дипломном проектировании.
В 1-й главе учебного пособия рассмотрены вопросы представления данных в ЭВМ, основные коды двоичных и двоично-десятичных алгебраических чисел, методы и алгоритмы выполнения операций сложения, вычитания, умножения и деления. Описаны также способы контроля правильности выполнения операций пересылки, сдвига, сложения и вычитания на основе использования сверток по мод. 2 и по мод. 3.
Во 2-й главе учебного пособия рассмотрены вопросы логического и схемотехнического проектирования цифровых устройств. Представлены разделы применения алгебры логики для решения задач анализа и синтеза логических схем, системы цифровых логических элементов, интегральные триггеры, основные функциональные узлы ЭВМ.
|
|
|
В 3-й главе учебного пособия рассмотрены назначение, принцип действия, структурные и функциональные схемы основных функциональных устройств, входящих в состав ЭВМ. Изложены методика и примеры проектирования основных блоков арифметическо-логического устройства и устройства управления.
В 4-й главе учебного пособия рассмотрены назначение, принцип действия, структурные и функциональные схемы основных типов микропроцессоров (МП) и соответствующих микропроцессорных комплектов (МП-комплектов), на основе которых строятся современные универсальные и специализированные ЭВМ и системы. Изложены методика и примеры проектирования МП-систем для использования в АСОИУ.
1. АРИФМЕТИЧЕСКИЕ ОСНОВЫ ЭВМ
1. 1. Основные форматы чисел
В ЭВМ выполняется обработка следующих видов данных: двоичных чисел, десятичных чисел и символьных данных.
Для представления всех видов данных в ЭВМ используются различные форматы.
Числа могут представляться в форме с фиксированной запятой и в форме с плавающей запятой. Для формы с фиксированной запятой форматы чисел будут различными для дробных и целых чисел.
Если А = 3Н, а1 а2 а3......... аn
аn = {0, 1} - двоичные цифры
| A | < 1, то формат (разрядная сетка) имеет следующий вид:
| № разряда | .......... | n | ||||
| Значение | ЗНАК | 2-1 | 2-2 | 2-3 | .......... | 2-n |
Положение запятой фиксируется перед разрядом с весом 2-1 .
Формат целого числа для |A| > 1 выглядит следующим образом:
| № разряда | n | n-1 | .......... | |||
| Значение | ЗНАК | 2n-1 | .......... | 22 | 21 | 20 |
Положение запятой фиксировано после разряда с весом 20.
Числа с плавающей запятой хранятся в памяти ЭВМ в нормализованном виде: a=А∙ 10а, где А - мантисса, 10 - основание системы счисления, а - порядок.
|
|
|
Мантисса должна удовлетворять следующему требованию:
1/10≤ │ A│ < 1, для двоичной системы │ А│ ≥ 2-1
Разрядная сетка (формат) такого числа имеет следующий вид:
| Знак порядка | Порядок | Знак числа | Мантисса |
| 2m........ 22 21 20 | 2-1 2-2............ 2-n |
В современных ЭВМ принято, что формат данных должен быть кратным байту — восьми двоичным разрядам.
Десятичные числа в ЭВМ изображаются с помощью двоично-десятичных кодов. Каждая десятичная цифра при этом представляется четырьмя двоичными разрядами, т. е. в одном байте помещается две десятичные цифры.
1. 2. Машинные коды алгебраических чисел
В ЭВМ используются, в основном, следующие коды чисел: прямой, обратный и дополнительный.
Если А — число с фиксированной запятой, |A| < 1;
[A]п — прямой код числа, который образуется по следующему правилу:
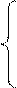 А, при А ≥ 0,
А, при А ≥ 0,
[A]п = (1. 1)
1 – A, при А < 0.
В машинных кодах знаки чисел отображаются с помощью двоичных цифр. Принято обозначать
ЗН. ”+”: = 0.; ЗН. ” — ”: = 1.
Пример. А= +. 101101; [A]п = 0. 101101
А= -. 101101; [A]п = _1. 000000
-. 101101
1. 101101
Представление чисел в прямом коде используется в ЭВМ при вводе и выводе, при хранении данных в ЭВМ (не всегда). Достоинством прямого кода является простота и привычность представления чисел в виде модуля числа и знака. Однако применение прямого кода для реализации алгебраических операций не очень удобно. Рассмотрим примеры выполнения операций сложения и вычитания в прямых кодах.
S1 = A + B; S2 = A - B; A=37/64; B=19/64.
A= +. 100101; B= +. 010011
111 – переносы 1 – заем
[A]п = 0. 100101 [A]п = 0. 100101
[B]п = 0. 010011 [B]п = 0. 010011
|
|
|
[S1]п = 0. 111000 [S2]п = 0. 010010
S1=56/64 S2=18/64
Как следует из этих примеров, сложение и вычитание различаются правилами образования переноса и заема. Это означает, что при разработке схем арифметического блока нужно будет строить не только сумматоры, но и вычитатели, т. е. специальные схемы, реализующие операцию вычитание. Такое техническое решение приведет к увеличению аппаратуры и практически не применяется.
Более широко для реализации алгебраических операций используются специальные коды, которые позволяют заменить операцию вычитание — сложением. При этом оказывается возможным при построении арифметических устройств использовать только сумматоры.
Обратный код числа образуется по следующему правилу:
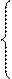 [A]о = [A]п, при А≥ 0,
[A]о = [A]п, при А≥ 0,
[A]о = (1. 2)
[A]о = 10 + A - 10-n, при А< 0
Например, А = -. 101101
[A]о = _10. 000000
. 101101
_1. 010011
. 000001
1. 010010.
Как видно из этого примера для получения обратного кода все цифры числа инвертируются. По этому же правилу осуществляется перевод обратного кода в прямой код.
Дополнительный код числа образуется по следующему правилу:
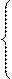 [A]п, при А ≥ 0
[A]п, при А ≥ 0
[A]д = (1. 3)
10 + A, при А< 0
Пример образования дополнительного кода отрицательного числа
А= -7/16 = -0. 0111 [A]д = _10. 0000
. 0111
1. 1001
Анализ правил образования обратного кода (1. 2) и дополнительного кода (1. 3) показывает, что для двоичной системы счисления является справедливым следующее соотношение:
|
|
|
[A]д = [A]о + 2-n. (1. 4)
На практике для нахождения дополнительного кода используют соотношение (1. 4), а не (1. 3).
|
|
|


