 |
1.5.1. Алгоритм типа ПП
|
|
|
|
Основной особенностью этого алгоритма является то, что он аналогичен методу десятичного ручного счета. Как известно, ручное сложение-вычитание выполняется по следующим правилам:
- вычисления осуществляются над модулями чисел;
- действие над модулями определяется на основе анализа вычислительной операции (действия ) и знаков чисел;
- выполняется действие над модулями;
- если действие над модулями вычитание, то из большего модуля вычитается меньший;
- знак результата определяется логическим способом в зависимости от действия над модулями, соотношения модулей и знаков исходных чисел.
Рассмотрим S=A ± B ï A ê < 1 ê B ê < 1 A≠ 0 B≠ 0
Для того, чтобы формализовать постановку задачи, введем обозначения:
Действие сложение - D: =0
Действие вычитание - D: =1
Сложение модулей - DM: =0
Вычитание модулей - DM: =1
Знак числа - ¢ +¢: =0
Знак числа - ¢ -¢: =1
Соотношение ê A ê ³ ê B ê соответствует W: =1
При ê A ê < ê B ê принято W: =0
Зададим условия этой задачи в виде таблицы истинности (табл. 1. 1), в которой описаны все варианты исходных данных.
Таблица 1. 1
| ЗН A | ЗН B | D | DM | ЗН S | |
|
|
|
|
| W: =1 | W: =0 |
В этой таблице истинности входными переменными являются ЗНА, ЗНВ, D, а выходными переменными - DM и ЗНS. После анализа данных в таблице можно сделать заключение, что действие над модулями DM является двоичной суммой трех входных переменных, а именно
|
|
|
DM = SM ( ЗНА, ЗНВ, D) (1. 7)
Таким же образом составим логическое выражение для знака суммы
ЗНS: = W & ЗНA Ú  & DM &
& DM & 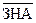 Ú
Ú  &
&  & ЗНA (1. 8)
& ЗНA (1. 8)
Сформулируем теперь в словесном виде алгоритм типа прямой-прямой (ПП), в соответствии с которым должны осуществляться преобразование и анализ кодов двоичных чисел при выполнении в АЛУ операции S = A ± B.
1) Ввод из ОЗУ в АЛУ [А]п и [В]п.
2) Определение DM по табл. 1. 1.
3) Если DM=0, то ê Sê = ê Аê +ê Вê,
если перенос p =1, то имеется переполнение разрядной сетки сумматора. В противном случае перенос p =0 и переход к п. 5), иначе
4) Если DM: =1, то выполняется вычитание модулей, причем
сначала определяется ê S ê = ê A ê - ê B ê и, если p =0, то ê A ê ³ ê B ê и переход к п. 5), иначе находится ê S ê = ê B ê - ï A ï и ê A ê < ê B ê
5) Определение ЗНS и запись результата в память.
Выполним, пользуясь этим алгоритмом,
пример:
Вычислить S = A + B A =. 01011 B = -. 10101
Следовательно [A]п = 0. 01011 [B]п = 1. 10101
Определим DM. Так как D: = 0 ЗНA: =0 ЗНB: =1,
то на основании (1. 1)
DM = SM ( 0, 0, 1) = 1
Теперь выполним вычитание модулей
ï A ê _=. 0 1 0 1 1
ê B ê =. 1 0 1 0 1
1. 1 0 1 1 0
так как р=1, то ê Aê < ê Bê и следует выполнить вычитание
модулей в обратном порядке:
ê B ê =. 1 0 1 0 1
-
ê A ê =. 0 1 0 1 1
|
|
|
ê S ê =. 0 1 0 1 0
Очевидно, что знак результата ЗНS = ЗНВ.
В память должен заноситься прямой код результата, т. е.
[S]п = 1. 0 1 0 1 0
В обычной записи сумма выглядит следующим образом:
S = -. 0 1 0 1 0
Выполним некоторую качественную оценку данного алгоритма. . Достоинством является то, что числа вводятся в память в прямых кодах и все вычислительные операции выполняются также в прямых кодах. Благодаря этому отсутствуют промежуточные преобразования кодов, что способствует повышению быстродействия.
Недостатком является необходимость использовать в АЛУ, кроме сумматоров, многоразрядные вычитатели, что приводит к увеличению оборудования.
|
|
|


