Плоская система сходящихся сил

Аксиомы статики

Аксиома 1. Свободное абсолютно твердое тело находится в равновесии под действием двух сил, тогда и только тогда, когда силы действуют по одной прямой в противоположные стороны и имеют равные модули.

Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменится, если к ней присоединить или от нее отбросить систему сил эквивалентную нулю.

{ , , , … } <=> { , , , … , , , , … };

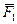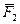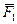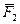{ , , , … } <=> 0

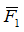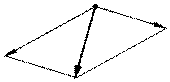
Аксиома 3. Две силы, приложенные в одной точке тела, эквивалентны равнодействующей, приложенной в той же точке и определяемой как диагональ параллелограмма, построенного на силах как на сторонах.

{ , } <=>

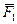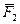Рис. 1.3

Аксиома 4. Силы взаимодействия двух тел равны по величине и направлены по одной прямой в противоположные стороны.

Тело называется свободным, если его перемещения в пространстве ничем не ограничены. Если на перемещение точек тела накладываются ограничения, то тело называется несвободным или связанным. Материальные тела, ограничивающие перемещения данного тела называются связями. Сила, с которой связь действует на данное тело, называется реакцией связи. Сила действует на связь, а реакция связи на тело.

Аксиома 5. (Аксиома освобождения от связей). Равновесие тела не нарушится, если наложенные на него связи заменить реакциями связей.

Аксиома 6. (Аксиома о затвердевании). Равновесие деформируемого тела не изменится, если на него наложить дополнительные связи или оно станет абсолютно твердым.

 

Следствия из аксиом

Следствие 1. Силу, приложенную к абсолютно твердому телу, можно переносить в любую точку ее линии действия. При этом действие силы на тело не изменится.

Доказательство:

Пусть на твердое тело действует сила 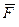, приложенная к точке А (рис. 1.4). Приложим в некоторой точке В линии действия силы F систему сил { 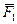, 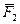} <=> 0, что допускается на основании Аксиомы 2. Примем 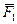= = 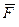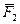. В результате получим систему сил { , , } <=> .

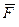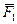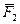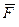Заметим, что { 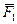, 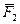} <=> 0, на основании аксиомы 2 эту систему сил можно отбросить. Получаем <=>{ , , }<=> .

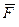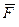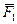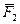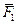Вывод: Сила является скользящим вектором.

Следствие 2. Теорема о необходимом условии равновесия тела, находящимся под действием трех непараллельных сил, лежащих в одной плоскости.

Если свободное тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

 

Доказательство:

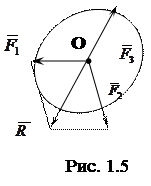Пусть к телу приложены три силы 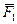, , 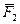(рис. 1.5). { 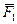, , 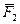} <=> 0. По­скольку линии действия сил непараллельны, то любые две из них (пусть 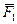и 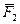) пересекутся в некоторой точке О. Перенесем F₁ и F₂ в точку О и заменим эти силы равнодействующей 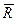. Получим { 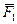, , 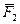} <=> { 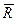, }, а для того чтобы тело находилось в равновесии, необходимо выполнение условия: 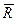= , и они должны быть направлены по одной прямой в противоположные стороны. То есть линия действия силы должна проходить через точку пересечения линий действия сил 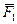и .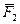

 

 

Лекция 2

Виды связей и их реакции

При решении технических задач возникает необходимость поиска реакций различных связей. Общее правило, которое следует применять, состоит в следующем: если ограничиваются перемещения какой-либо точки тела, то реакцию следует прикладывать в этой точке в сторону, противоположную направлению, в котором ограничивается перемещение.

 

Основные типы связей:

1. Гладкая поверхность или опора. Гладкой считается поверхность, трением о которую можно пренебречь. Реакция гладкой поверхности сводится только к реакции , направленной по общей нормали к контактирующим поверхностям, в предположении, что эта нормаль существует (рис. 2.1.а). Если общей нормали не существует, то есть одна из поверхностей имеет угловую точку или «заострение», реакция направлена по нормали к другой поверхности (рис. 2.1.б).

Рис. 2.1. а

Рис. 2.1 б

 

2. Шероховатая поверхность - это поверхность трением, по которой пренебрегать нельзя. Реакция 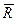шероховатой поверхности складывается из нормальной реакции и силы трения . (рис 2.2). Модуль R определяется по формуле:

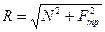. (2.1)

3. Гибкая связь. К этому типу связи относятся связи, осуществляемые с помощью цепи, троса, каната и т. д. Реакция такой связи всегда направлена вдоль связи (рис. 2.3).

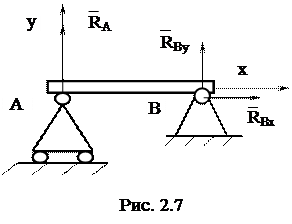
4. Цилиндрический шарнир (рис. 2.4) и подшипник (опора В рис.2.5). Цилиндрическим шарниром на­зывается соединение двух или более тел по­средством цилиндрического стержня, так называемого пальца, вставленного в отверстия в этих телах. Цилиндрический шарнир препятствует перемеще­нию по любому направ­лению в плоскости ХОY. Реакция 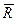неподвижного цилиндрического шарнира (шарнирно-неподвижной опоры) представляется в виде неиз­вестных составляющих 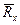и , линии действия которых парал­лельны или совпадают с осями ко­ординат (рис. 2.4).

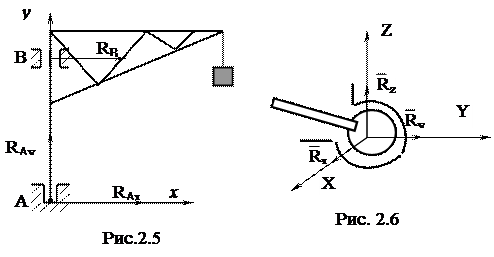
5. Подпятник (опора А рис. 2.5) и сферический шарнир (рис. 2.6). Та­кой вид связи можно представить в виде стержня, имеющего на конце сферическую поверхность, которая крепится в опоре, представляющей собой часть сферической полости. Сферический шарнир препятствует пере­мещению по любому направлению в пространстве, поэтому реакция его представляется в виде трех составляющих 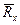, , , параллельных соответ­ствующим координатным осям.

6.

Шарнирно-подвижная опора. Этот вид связи конструктивно выполняется в виде цилиндрического шарнира, кото­рый может свободно переме­щаться вдоль поверхности. Реакция шарнирно-подвижной опоры всегда направлена перпендикулярно опорной поверх­ности (опора А рис. 2.7).

7. Шарнирно-неподвижная опора. Реакция 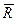шарнирно-неподвиж­ной опоры представляется в виде неизвестных составляющих 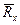и , линии действия которых па­раллельны или совпадают с осями коорди­нат (опора В рис. 2.7).

8. Невесомый стержень (прямолинейный или криволинейный), закреплен­ный по концам шарнирами. Реакция такого стержня является определен­ной и направлена вдоль линии, соединяющей центры шарниров (рис. 2.8).

 

 

 

9. Жесткая заделка. Это необычный вид связи, так как кроме препятствия перемещению в плоскости ХОY, жесткая заделка препятствует повороту стержня (балки) относительно точки А. Поэтому реакция связи сводится не только к реакции R (R_аx, R_аy), но и к реактивному моменту М_ра (рис. 2.9).

Плоская система сходящихся сил

Системой сходящихся сил называется система сил, линии, действия которых пересекаются в одной точке. Эту точку называют точкой схода сил.

123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: