Способы задания движения точки

Задать движение точки – значит задать ее положение относительно некоторой системы отсчета в любой момент времени.

Естественный способ задания движения точки (рис. 4.1). Задать движение точки естественным образом – значит:

а) задать траекторию движения точки в некоторой системе отсчета;

б) на траектории выбрать начало О и положительное направление отсчета расстояний S = OM;

в) указать закон движения точки S=f(t), а также начало отсчета времени t₀.

Функция S=f(t) должна быть однозначной, непрерывной, дифференцируемой.

Закон движения точки может быть задан графически: кривой, отражающей зависимость S от t. Это графическое изображение закона движения точки называют графиком движения точки.

 

 

Рис. 4.1

На рис. 4.1 t - ось, касательная к траектории движения точки, направленная в сторону положительного отсчета расстояния S; n – нормаль к траектории дви­жения точки, направленная в сторону вогнутости траектории, b – бинормаль, перпендикулярна к первым двум так, чтобы она образовала с ними правую тройку. Эти оси называются естественными осями.

Координатный способ. Положение точки в пространстве трех измерений можно однозначно определить, задав три ее координаты в некоторой системе отсчета. Задать движение точки в координатной форме – значит задать координаты этой точки как функции времени: x=f(t), y=f(t), z=f(t). Эти уравне­ния называются уравнениями движения точки.

 

Скорость точки

Пусть движение точки задано естественным способом, и пусть в некоторый момент времени t точка занимала на траектории положение М, а в некоторый момент времени t₁ – положение М₁ (рис. 4.2). Вектор называется векто­ром перемещения точки за промежуток времени: . Отношение вектора перемещения к промежутку времени, за который произошло это перемещение, называется вектором средней скорости точки за промежуток времени .

. (4.1)

Вектором скорости в точке в момент времени t называется предел вектора средней скорости при стремлении промежутка к нулю,

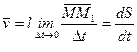. (4.2)

То есть скорость материальной точки при движении по произвольной кри­волинейной траектории направлена по касательной к траектории в сторону движения.

 

Рис. 4.2

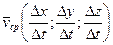Если движение точки задано координатным способом, и движущаяся точка в момент времени t занимала положение М (x, y, z), а в момент времени t₁ – положение М₁ (x+Dx, y+Dy, z+Dz), то вектор средней скорости имеет координаты , а вектор скорости в момент времени t – координаты .

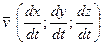Проекции вектора скорости на оси координат: , , . Модуль находим по формуле:

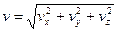, (4.3)

Косинусы углов, образуемых вектором скорости с осями координат, можно найти из соотношений , , .

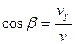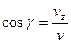Ускорение точки

Величину, определяющую изменение вектора скорости точки в зависимости от времени, называют ускорением точки.

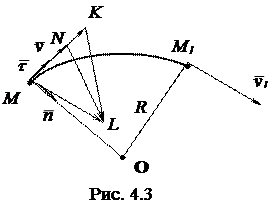
Пусть движение точки задано естественным способом (рис. 4.3), а траекто­рией движения точки является дуга окружности. Допустим, что в некоторый момент времени t точка занимала положение М на траектории и имела скорость v, а в момент времени t₁=t + Dt – положение М₁ и скорость v₁. Перенесем век­тор в точку М и построим вектор:

. (4.4)

Вектор 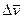называется вектором приращения скорости. Вектор равен от­ношению приращения скорости 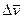к соответствующему приращению времени Dt.

. (4.5)

 

Вектором ускорения точки в момент времени t называется предел вектора среднего ускорения при стремлении промежутка времени Dt к нулю.

. (4.6)

От точки М отложим по линии действия вектора вектор 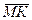, равный по абсолютной величине вектору . Приращение скорости представим в виде:

. (4.7)

Тогда

. (4.8)

Вычислим первый предел. Для этого введем на касательной к траектории движения точки в точке М единичный вектор .

, (4.9)

где Dv_a – приращение алгебраической величины скорости.

. (4.10)

- тангенциальное (касательное) ускорение точки, характеризующее изменение алгебраической величины вектора скорости.

Второй предел

. (4.11)

Вектор направлен перпендикулярно касательной к траектории движения точки, причем в сторону ее вогнутости. Вектор носит название нормального ускорения точки и характеризует изменение направления вектора скорости. Введем на нормали единичный вектор n и запишем формулу для полного ускорения точки

. (4.12)

 

Модуль и направляющие косинусы полного ускорения найдутся по формулам:

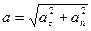, (4.13)

(4.14)

где a - угол между направлением вектора полного ускорения и единичного вектора t, b - угол между направлением вектора полного ускорения и единичного вектора n.

 

Лекция 5

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: