 |
Понятие о моменте количества движения
|
|
|
|
Иногда при изучении движения точки вместо изменения самого вектора 
(
) оказывается удобным рассматривать изменение его момента. Момент вектора относительно какого-либо центра О или оси z обозначается Мо(mv) или Мz(mv) и называется соответственно моментом количества движения или кинетическим моментом точки относительно этого центра или оси. Вычисляется момент количества движения так же, как и момент силы.
Производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра
. (7.16)
Аналогичная зависимость имеет место для моментов вектора ()и силы 
относительно какой-либо оси z.
Лекция 8
Кинетическая энергия
Кроме количества движения основной мерой механического движения является кинетическая энергия. Кинетической энергией материальной точки называется скалярная величина, равная
. (8.1)
Кинетическая энергия – есть величина положительная при любых значениях скорости, при 
. Если 
, то точка покоится относительно инерциальной системы отсчета и ее кинетическая энергия равна нулю.
Теорема. Изменение кинетической энергии материальной точки за некоторый промежуток времени равно работе приложенной к точке силы за тот же промежуток времени.
Доказательство:
.
Умножим обе части скалярно на v, получим:
, где a - угол между направлением вектора скорости и направлением линии действия силы. Полученную запись представим в виде
.
Правая часть этого равенства представляет собой элементарную работу силы F. Интегрируя полученное выражение в соответствующих пределах, получим:
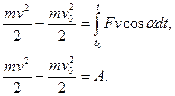(8.2)
Потенциальная энергия
|
|
|
Часть (ограниченная или неограниченная) пространства, в каждой точке которого на находящуюся там материальную точку действует некоторая сила, зависящая только от положения этой точки, то есть ее координат x, y, z, называется силовым полем. Проекции X, Y, Z силы поля на координатные оси являются некоторыми однозначными и непрерывными функциями от x, y, z. То есть 
, 
, 
. Допустим, что существует такая функция координат U(x, y, z), частные производные которой по координатам равны проекциям силы поля на соответствующие координатные оси
, 
, 
. (8.3)
Такая функция U называется силовой функцией данного силового поля, а силовое поле в этом случае называется потенциальным. Найдем выражение элементарной работы силы потенциального поля:
,
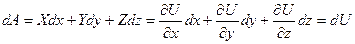то есть элементарная работа силы потенциального поля равна полному дифференциалу силовой функции.
Следовательно, работа на конечном пути, когда точка приложения силы перемещается из положения М0 в положение М, выразится так:
, (8.4)
то есть работа силы потенциального поля равна разности значений силовой функции в конечной и начальной точках пути и, следовательно, не зависит ни от вида, ни от длины траектории, по которой перемещается точка приложения силы из положения М0 в положение М.
Отсюда следует, что в случае однозначной силовой функции U работа силы потенциального поля на всякой замкнутой траектории равна нулю.
Пусть точка М0 (x 0, y 0, z 0 ) будет какая-либо произвольно выбранная неподвижная (нулевая) точка, в которой силовая функция имеет значение U(x 0, y 0, z 0 ).
Работа, производимая силой при перемещении материальной точки из положения М в «нулевую точку» М0, называется потенциальной энергией в точке М.
. (8.5)
Очевидно, что в нулевой точке М0 потенциальная энергия равна нулю.
Закон сохранения энергии
Пусть М1 и М2 будут двумя различными положениями материальной точки, движущейся в потенциальном силовом поле, и U1 и U2 – соответствующие значения силовой функции в этих точках. Напишем уравнение, выражающее теорему о кинетической энергии:
|
|
|
,
где v1 и v2 – скорости движущейся точки в положениях М1 и М2. Но так как работа А равна разности значений силовой функции в конечном и начальном положениях движущейся точки, то
. (8.6)
Тогда потенциальная энергия в точках М1 и М 2 будет выражаться так:
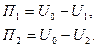
Отсюда
Подставляя полученные значения в выражение (8.5) получим:
,
или
,
то есть
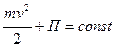. (8.7)
Следовательно, при движении материальной точки в потенциальном силовом поле сумма кинетической и потенциальной энергии остается постоянной.
|
|
|
