Произвольная плоская система сил

Лемма Пуансо. Действие силы на твердое тело не изменится, если перенести эту силу параллельно своему первоначальному положению в любую точку тела, приложив при этом к телу пару с моментом, равным моменту исходной силы относительно этой точки.

 

Доказательство:

Пусть сила 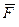приложена к телу в некоторой его точке А (рис. 3.8). Приложим в произвольной точке О параллельно направлению линии действия силы 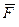две силы и , равные по модулю силе 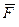и направленные в противоположные стороны. Полученная система сил { 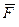, , } <=> 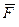. Эту систему сил можно считать состоящей из силы , полученной параллельным переносом силы 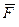в точку О, и пары (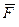, ), называемой присоединенной парой с моментом, равным моменту силы 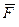относительно точки О.

 

 

Рис. 3.8

 

Приведение произвольной плоской системы сил к точке (основная теорема статики для произвольной плоской системы сил)

Рассмотрим на примере трех сил. Пусть к телу в точках А, В, С приложена плоская система сил { 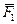, , } (рис. 3.9). Выберем произвольную точку О, перенесем в нее силы 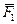, , . Согласно лемме Пуансо получим сходящуюся систему сил { , , } и систему пар (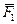, ), (, ), (, ) с моментами М₁, М₂, М₃, равными моментам сил 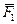, , относительно точки О.

Сложив 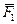, , по правилу многоугольника, получим:

. (3.7)

Вектор , равный геометрической сумме сил системы, называется главным вектором данной системы сил.

Теперь сложим пары сил, в результате получим пару сил с моментом

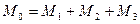. (3.8)

М₀ – равен алгебраической сумме моментов сил и называется главным моментом системы сил относительно точки.

 

 

Рис. 3.9

Теорема Вариньона. Если система сил приводится к равнодействующей, то момент равнодействующей относительно любой точки равен сумме моментов всех сил системы относительно той же точки.

Доказательство:

Пусть система сил { , , } имеет равнодействующую 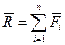(рис. 3.10), приложенную в некоторой точке О₁ плоскости действия сил. Перенесем вектор в точку О, при этом согласно лемме Пуансо необходимо добавить пару (, ) с моментом М₀=М( ). Но М₀ – главный момент системы сил относительно точки О, который равен алгебраической сумме моментов всех сил системы относительно этой точки: . Следовательно .

 

Рис. 3.10

Следствия из теоремы:

1. Главный вектор не изменится при изменении центра приведения.

2. Главный момент при перемене центра приведения изменится на величину момента силы , приложенной в точке О, относительно нового центра.

Условия равновесия

Свободное твердое тело под действием произвольной плоской системы сил находится в равновесии, если главный вектор и главный момент этой системы относительно любой точки равны нулю: =0, М₀=0. Разложим по осям получим:

(3.9)

Условие равновесия для произвольной пространственной системы сил:

(3.10)

 

Лекция 4

Кинематика

В кинематике изучается движение материальных тел в пространстве с гео­метрической точки зрения, без учета сил, определяющих это движение.

Всякое движение тел совершается в пространстве и во времени. Движение тел в пространстве рассматривается относительно выбранной системы коорди­нат, которая в свою очередь связана с каким-либо телом, называемым телом от­счета. Тело отсчета и связанная с ним система координат называются системой отсчета. Пространство в механике рассматривается как трехмерное. За единицу длины при измерении расстояний принимается метр. Время в механике счита­ется универсальным, то есть протекающим одинаково во всех системах отсчета. За единицу времени принимается секунда.

 

Кинематика точки

Непрерывная кривая, описываемая движущейся точкой в пространстве, называется траекторией точки.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: