 |
Пара сил. Момент пары сил на плоскости
|
|
|
|
Парой сил называется система двух сил 
и 
(рис. 3.3), приложенных к твердому телу, удовлетворяющая следующим условиям:
1. Линии действия сил параллельны.
2. Модули сил равны (F = F’).
3. Направления действия сил противоположны.
Плоскость, на которой лежат линии действия пары сил, называется плоскостью действия пары. Расстояние h между линиями действия сил и называется плечом пары. Совокупность пар, приложенных к телу, называется системой пар.
Пара сил, приложенная к телу, стремится сообщить ему некоторое вращение. Вращательный эффект пары характеризуется ее моментом. Моментом пары сил называется произведение модуля одной из сил пары на ее плечо, взятое со знаком «+» или «-»
. (3.3)
Момент пары считается положительным, когда пара стремится повернуть тело против хода часовой стрелки, и отрицательным - когда по ходу часовой стрелки.
Теорема об эквивалентных парах. Две пары сил, лежащие на одной плоскости и имеющие равные алгебраические величины моментов, эквивалентны.
Доказательство:
 |
Пусть (
, ) и (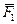
, 
) – две пары сил, лежащие в одной плоскости и имеющие равные моменты М (, ) =М(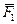, ). Продолжим линии действия сил пересечения друг с другом (рис. 3.4). Перенесем силы 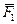и по линиям действия в точки А и В и разложим каждую из них на составляющие. Получим: { , } <=> {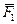 
, 
, 
, 
}. Из построения имеем =- , =- , так как и направлены по одной прямой, то { , }. <=> 0, а { , } <=> { , }.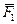
Докажем эквивалентность пар (, ) и (, ). Для этого достаточно доказать, что = 
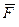. Плечи пар (, ) и (, ) равны; момент пары (
, 
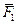) численно равен удвоенной площади треугольника АВС, а момент пары (, ) – удвоенной площади треугольника АВD. Но площади этих треугольников равны, так как у них общее основание и равные высоты, опущенные из вершин С и D, то есть F2h=F1h1, но так как Fh=F1h1, то F2h=Fh, следовательно, = 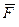, тогда (, ) <=> (, ) и (, ) <=> (, ).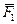
|
|
|
Следствия из теоремы об эквивалентных парах:
1. Пару сил можно переносить в любое место плоскости ее действия.
2. Действие пары сил на тело не изменится, если изменить значения модуля силы и плеча, оставляя величину момента прежней.
3. Пару сил можно переносить в плоскость, параллельную плоскости действия.
Теорема о сложении пар сил. Пары сил, лежащие в одной плоскости можно складывать. В результате сложения получается лежащая на той же плоскости пара сил с моментом, равным алгебраической сумме моментов слагаемых пар.
Доказательство:
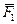Докажем для двух пар. Пусть (, ) и (, ) – пары, лежащие на одной плоскости и имеющие моменты М1 = F1h1 и М2 = F2h2. Возьмем произвольный отрезок АВ = h (рис. 3.5). На основании теоремы об эквивалентных парах можно заменить введенные пары эквивалентными им парами (, ) и (
, 
), имеющими плечо h. 
. Сложив силы в точке А, получим = + ; в точке В – 
= + ; =- .
.
Справедливо для любого числа пар:
. (3.4)
Рис. 3.5
Равновесие рычага
Рычагом называется твердое тело, вращающеесявокруг неподвижной оси и находящееся под действием сил, лежащих в плоскости перпендикулярной к этой оси. Если на рычаг действует сходящаяся система сил, то равновесие рычага достигается, когда линия действия равнодействующей проходит через точку О (рис. 3.6), а алгебраическая сумма моментов приложенных к нему сил относительно точки О равна нулю:
(3.5)
Рассмотрим случай, когда на рычаг действует система параллельных сил, лежащих в одной плоскости. Приложенная к рычагу система параллельных сил может быть приведена или к одной равнодействующей, или к паре.
 |
Рис. 3.6
Сложим все силы, направленные вверх: 
, и вниз: 
, соответственно. Найти точки приложения равнодействующих можно по формулам
|
|
|
(3.6)
В итоге возможны три случая:
1) 
, тогда система сводится к одной равнодействующей.
2) 
- система не имеет равнодействующей и сводится к паре сил.
3) , и они направлены по одной прямой, тогда система представляет собой уравновешенную систему сил.
Если система параллельных сил, приложенная к рычагу, сводится к паре, то равновесия рычага быть не может, так как реакция шарнира О (рис. 3.7) не может уравновесить пару. То есть, при равновесии рычага приложенная к нему система параллельных сил приводится к равнодействующей силе, проходящей через неподвижную точку рычага.
|
|
|
