Вращение твердого тела вокруг неподвижной оси

Вращательным движением твердого тела называется движение, при котором две его точки А и В остаются неподвижными. Так как тело абсолютно твердое, то вместе с точками А и В будут неподвижны все точки, лежащие на прямой АВ. Эта прямая называется осью вращения (рис. 5.2). Все точки тела при вращательном движении описывают дуги окружностей с центрами в основаниях перпендикуляров, опущенных из этих точек на ось вращения.

Проведем через ось вращения две полуплоскости, одну из которых зафиксируем, а другую свяжем с телом. Двугранный угол j, угол поворота, между этими полуплоскостями будет однозначно определять положение тела. Задавая значение угла j в каждый момент времени t, можно тем самым определить положение тела для любого t. Уравнение

(5.3)

носит название закона вращательного движения тела. Функция (5.3) предполагается дважды дифференцируемой.

Главными кинематическими характеристиками вращательного движения тела будут угловая скорость w (с^-1) и угловое ускорение e (с^-2).

Пусть за некоторый промежуток времени 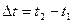угол j получит приращение . Величина называется средней угловой скоростью тела. Предел, к которому стремится средняя угловая скорость при Dt®0, называется угловой скоростью тела в данный момент времени t.

. (5.4)

Если тело совершает вращательное движение по произвольному закону, то угловая скорость является функцией времени: .

Пусть за некоторый промежуток времени 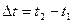угловая скорость получила приращение . Величина называется средним угловым ускорением. Предел, к которому стремится среднее ускорение при Dt® 0, называется угловым ускорением в данный момент времени t.

. (5.5)

Связь угловых характеристик вращающегося твердого тела с линейными кинематическими характеристиками вращающегося тела

Как уже отмечалось, траекторией любой точки М вращающегося тела является дуга окружности, лежащая в плоскости перпендикулярной оси вращения. Радиус этой окружности равен расстоянию от точки до оси. Рассмотрим траекторию движения некоторой точки М тела, вращающегося вокруг оси, перпендикулярной плоскости рисунка и проходящей через центр окружности (рис. 5.3).

 

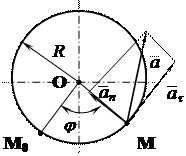Рис. 5.3

Если отсчитывать дуговую координату s точки М от ее начального положе­ния М₀ в направлении возрастания угла j, то закон движения точки М по дуге окружности будет иметь вид . В этом случае алгебраическое значение скорости определяется по формуле:

. (5.6)

Найдем ускорение точки М:

.

Продифференцировав (5.6) по времени, определим алгебраическую величину касательного ускорения:

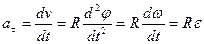. (5.7)

Нормальное ускорение получим, подставляя (5.6) в выражение для нормального ускорения:

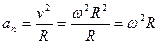. (5.8)

Следовательно, для вектора ускорения имеем:

. (5.9)

Для модуля ускорения точки М имеем формулу:

. (5.10)

Из выражений (5.6) и (5.10) следует, что линейные кинематические характеристики точек зависят от угловых характеристик вращающегося твердого тела, а коэффициентом пропорциональности является радиус вращения.

 

Сложное движение точки

До сих пор движение точки рассматривалось по отношению к неподвижной системе координат, но в ряде случаев целесообразно изучать движение точки одновременно в двух системах отсчёта, из которых одна является неподвижной, а другая - подвижной, совершающей определённым образом движение относительно первой. Движение точки, в этом случае, называют сложным.

На рис. 5.4 изображены две системы координат: неподвижная Oxyz и подвижная O₁x₁y₁z₁. Движение, совершаемое точкой М по отношению к подвижной системе координат O₁x₁y₁z₁ называется относительным движением. Движение подвижной системы отсчёта O₁x₁y₁z₁ и всех точек пространства с ней связанных по отношению к неподвижной системе Oxyz называется переносным движением. Движение точки М относительно неподвижной системы координат Oxyz называется абсолютным.

Скорость точки М по отношению к неподвижной системе координат называется абсолютной скоростью точки.

Скорость точки М по отношению к подвижной системе координат называется относительной скоростью точки.

Переносной скоростью точки М называется скорость подвижной системы относительно неподвижной, в которой в данный момент времени находится движущаяся точка М.

Теорема о скорости точки в сложном движении.

Вектор абсолютной скорости точки в данный момент времени равен геометрической сумме векторов относительной и переносной скоростей в тот же момент времени.

Доказательство.

Пусть тело S, неизменно связанная с ним подвижная система отсчёта O₁x₁y₁z₁ и точка М₁ занимают в момент времени t₁ положение I (рис. 5.5) относительно неподвижной системы Oxyz. Пусть в момент времени t₂=t₁+Dt тело S и система O₁x₁y₁z₁ займут положение II, а точка М₁ перейдёт в точку М₂. Буквой М' обозначим положение той точки тела S, в которую переместится за время Dt его точка, совпадающая в момент t₁ с М₁.

Вектор изображает абсолютное перемещение точки, вектор относительное перемещение, вектор переносное перемещение точки за время Dt. Для этих векторов справедливо следующее равенство

. (5.11)

 

Разделив (5.11) почленно на Dt, получим

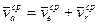, (5.12)

где - средняя абсолютная скорость;

- средняя переносная скорость;

- средняя относительная скорость.

Переходя в (5.12) к пределу при Dt стремящемся к нулю, получим

, или (5.13)

Теорема доказана.

Согласно доказанной теореме вектор абсолютной скорости изображается диагональю параллелограмма, построенного на векторах переносной и относительной скоростей. Модуль вычисляется по теореме косинусов

, (5.14)

где g - угол между векторами переносной и относительной скоростей.

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: