Скорость точки плоской фигуры

Теорема. Скорость любой точки В плоской фигуры в данный момент времени есть геометрическая сумма скорости некоторого полюса и скорости , возникающей вследствие вращения фигуры вокруг полюса, то есть

. (5.15)

 

Доказательство

Пусть фигура S (рис. 5.8) совершает плоское движение. Любое перемещение этой фигуры может быть составлено из поступательного перемещения вместе с полюсом А и поворота вокруг этого полюса.

Представим движение произвольной точки В как сложное: за переносное примем поступательное движение системы координат Ax₁y₁, за относительное - движение, совершаемое точкой В при вращении плоской фигуры вокруг полюса А. На основании теоремы о скорости точки в сложном движении имеем .

В этом выражении , , так как переносное движение поступательное, а , так как относительным будет движение точки В по окружности радиуса АВ. Следовательно , что и доказывает теорему.

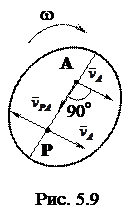
Мгновенный центр скоростей

Мгновенным центром скоростей называется такая точка плоской фигуры (или неизменно связанной с этой фигурой плоскости), скорость которой в данный момент времени равна нулю.

Пусть фигура S (рис. 5.9) совершает плоскопараллельное движение, причем угловая скорость этого движения не равна нулю. Примем произвольную точку А фигуры S за полюс. Повернём вектор скорости точки А вокруг его начала в сторону вращения на угол p/2 и отложим в полученном направлении отрезок АР . Действительно из (5.15) имеем 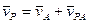, причем АР 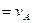, а направление вектора противоположно . Следовательно, и .

Приняв за полюс мгновенный центр скоростей, получим выражение для скорости произвольной точки А в виде: , но , тогда , АР, то есть скорости точек плоской фигуры в данный момент времени распределены таким образом, как если бы эта фигура вращалась вокруг мгновенного центра скоростей с угловой скоростью w.

Если А и В - произвольные точки тела, Р - мгновенный центр скоростей (рис. 5.10), то поскольку АР, ВР, получим

. (5.16)

Таким образом, скорости точек плоской фигуры прямо пропорциональны их расстояниям до мгновенного центра скоростей.

 

Лекция 6

Динамика

Динамика – раздел теоретической механики, изучающий движение матери­альных объектов и причины его вызывающие.

Движение тела считается известным, если известно движение каждой его точки; поэтому изучение динамики начинается с изучения движения матери­альной точки. Под материальной точкой понимают тело, размеры которого та­ковы, что различием в перемещениях отдельных его частиц можно пренебречь. Материальную точку можно рассматривать как геометрическую точку, имею­щую конечную массу.

 

Законы Галилея - Ньютона

Закон инерции. Изолированная материальная точка движется с нулевым ус­корением.

Первый закон указывает на одно из важнейших свойств материи – инерт­ность. Свойство инертности проявляется в способности тела сохранять свое движение при отсутствии внешних воздействий, а также изменять его под дей­ствием сил не мгновенно, а постепенно. Это изменение происходит тем мед­леннее, чем больше вещества содержится в теле.

Величина, являющаяся мерой инертности тела и определяющая количество вещества, содержащегося в теле, называется инертной массой тела.

Основной закон динамики. Модуль силы, действующий на материальную точку, равен произведению массы точки на модуль ее ускорения, а направление силы совпадает с направлением ускорения.

. (6.1)

Таким образом, причиной возникновения движения является сила.

Закон равенства действия и противодействия. Две материальные точки действуют друг на друга с силами, равными по модулю и направленными по прямой, соединяющей эти точки, в противоположные стороны.

. (6.2)

Следствие. Пусть к точке массы m приложена система сил { 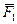, , 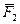,… }. Каждая сила сообщает точке ускорение , ускорение 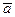, определяемое всей системой сил, равно:

. (6.4)

 

⇐ Предыдущая123456789Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: