 |
2.7.1. Пузырьковое кипение в большом объеме
|
|
|
|
2. 7. 1. Пузырьковое кипение в большом объеме
Для пузырькового кипения в условиях естественной конвекции, в качестве определяющей принимают температуру насыщения 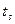 . Теплоотдача рассчитывается для следующих двух случаев:
. Теплоотдача рассчитывается для следующих двух случаев:
1) задана тепловая нагрузка q, Вт/м2:
 при
при 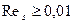 ; (9. 1)
; (9. 1)
 при
при  ; (9. 2)
; (9. 2)
2) задан температурній напор 
 при
при  ; (9. 3)
; (9. 3)
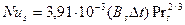 при
при  ; (9. 4)
; (9. 4)
здесь  ;
;  ;
;  ;
;  ; r -теплота парообразования, Дж/кг; Ts - температура насыщения, К;
; r -теплота парообразования, Дж/кг; Ts - температура насыщения, К;  ,
, 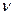 ,
, 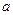 ,
,  ,
,  - теплопроводность, кинематическая вязкость, температуропроводность, удельная теплоемкость и поверхностное натяжение жидкости;
- теплопроводность, кинематическая вязкость, температуропроводность, удельная теплоемкость и поверхностное натяжение жидкости;  и
и  - плотность жидкости и пара.
- плотность жидкости и пара.
Формулы (9. 1) – (9. 4) пригодны при условии  ;
;  ; давление
; давление  Па;
Па;
 .
.
Для воды значения  ,
,  ,
,  приведены в табл. 15 приложения.
приведены в табл. 15 приложения.
Средний коэффициент теплоотдачи при пузырьковом кипении воды
 , (9. 5)
, (9. 5)
где  - давление насыщения, МПа; q - плотность теплового потока, Вт/м2; формула применима при
- давление насыщения, МПа; q - плотность теплового потока, Вт/м2; формула применима при  МПа.
МПа.
Первая критическая плотность теплового потока при пузырьковом кипении чистых неметаллических жидкостей на горизонтальных трубах и плитах
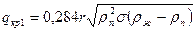 . (9. 6)
. (9. 6)
2. 7. 2. Пузырьковое кипение в трубах при вынужденной конвекции
При объемном паросодержании до 70 % теплоотдача при кипении характеризуется как конвекцией однофазной среды, так и процессом парообразования (двухфазное состояние). При малых тепловых нагрузках большее влияние оказывает конвекция однофазной жидкости, при больших парообразование.
|
|
|
Коэффициент теплоотдачи  при вынужденном течении кипящей жидкости в трубах можно определить следующим образом:
при вынужденном течении кипящей жидкости в трубах можно определить следующим образом:
если 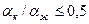 , то
, то
 , (9. 7)
, (9. 7)
где  - коэффициент теплоотдачи однофазной жидкости при турбулентном режиме течения, определяется по формуле (6. 18);
- коэффициент теплоотдачи однофазной жидкости при турбулентном режиме течения, определяется по формуле (6. 18); 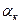 - коэффициент теплоотдачи при пузырьковом кипении, определяется по формулам (9. 1) - (9. 4);
- коэффициент теплоотдачи при пузырьковом кипении, определяется по формулам (9. 1) - (9. 4);
если 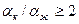 , то
, то
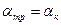 ; (9. 8)
; (9. 8)
если  , то
, то
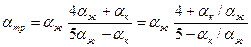 . (9. 9)
. (9. 9)
Для воды формулы (9. 7) – (9. 8) пригодны при давлении  МПа и объемном паросодержании
МПа и объемном паросодержании 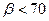 %.
%.
2. 7. 3. Пленочное кипение в большом объеме
Коэффициент теплоотдачи определяется из формулы
 , (9. 10)
, (9. 10)
где 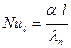 ;
; 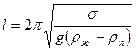 ;
;  ;
;  .
.
Значения С и n определяются следующим образом:
для вертикальной поверхности
 ;
;  ;
;
определяющая температура 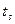 ;
;
для горизонтальной плоской поверхности
 ,
, 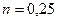 , если
, если  , и
, и
 ,
, 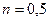 , если
, если  ;
;
определяющая температура 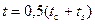 ;
;
для боковой поверхности горизонтальной круглой трубы с наружным диаметром d
 ;
; 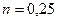 ;
;
определяющая температура 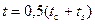 .
.
3. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ МЕЖДУ ТЕЛАМИ,
РАЗДЕЛЕННЫМИ ПРОЗРАЧНОЙ СРЕДОЙ
3. 1. Основные понятия и расчетные формулы
Теплообмен излучением - передача теплоты, связанная с превращением внутренней энергии тела в энергию электромагнитных волн (или фотонов) и последующим превращением последней во внутреннюю энергию других тел.
В инженерных расчетах теплообмен излучением между телами, разделенными прозрачной (диатермичной) средой, проводится в предположении о том, что излучающие поверхности - серые и их излучение - диффузное с постоянной плотностью на изотермических участках поверхности,
|
|
|
Серым телом называется тело, имеющее непрерывный спектр излучения, полностью подобный спектру абсолютно черного тела при той же температуре, его спектральный коэффициент теплового излучения е. постоянен во всем диапазоне длин волн от нуля до бесконечности и не зависит от температуры. Диффузное излучение характеризуется интенсивностью, не зависящей от направления.
При расчетах теплового излучения серых тел применяется понятие эффективного излучения, оно представляет собойсовокупность собственного Е излучения тела н отраженного Еотризлучения.
Поверхностная плотность потока собственного излучения тела, Вт/м2 имеющего абсолютную температуру Т, К,
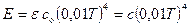 ; (10. 1)
; (10. 1)
здесь  - интегральный коэффициент теплового излучения - отношение плотностей потока излучения Е реального тела и абсолютно черного тела Ео или отношение коэффициентов лучеиспускания реального тела с и абсолютно черного тела
- интегральный коэффициент теплового излучения - отношение плотностей потока излучения Е реального тела и абсолютно черного тела Ео или отношение коэффициентов лучеиспускания реального тела с и абсолютно черного тела 
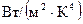 . Тогда для реального тела
. Тогда для реального тела
 . (10. 2)
. (10. 2)
Значение с изменяется от 0 до 5, 67,  изменяется от 0 до 1. Пренебрегая зависимостью
изменяется от 0 до 1. Пренебрегая зависимостью  от температуры, можно выбирать значения
от температуры, можно выбирать значения  из табл. 16 приложения.
из табл. 16 приложения.
Тепловой поток излучения  , Вт, между двумя телами, имеющими температуры
, Вт, между двумя телами, имеющими температуры  и
и 
 определяется и общем виде по формуле
определяется и общем виде по формуле
 , (10. 3)
, (10. 3)
где  - приведенный коэффициент теплового излучения системы двух тел; спр
- приведенный коэффициент теплового излучения системы двух тел; спр  - приведенный коэффициент лучеиспускания системы двух тел;
- приведенный коэффициент лучеиспускания системы двух тел; 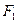 - площадь поверхности тела с температурой
- площадь поверхности тела с температурой  ;
; 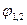 - средний угловой коэффициент лучеиспускания тела с температурой
- средний угловой коэффициент лучеиспускания тела с температурой  .
.
Средний угловой коэффициент лучеиспускания (коэффициент облученности) 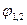 есть безразмерное число, меньшее единицы, которое показывает, какая доля от всего теплового потока
есть безразмерное число, меньшее единицы, которое показывает, какая доля от всего теплового потока  , излучаемого одним телом со всей своей поверхности во все стороны пространства, достигает поверхности другого тела, т. е.
, излучаемого одним телом со всей своей поверхности во все стороны пространства, достигает поверхности другого тела, т. е. 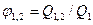 , где
, где  - поток от первого тела, достигший поверхности второго тела. Излучаемые потоки предполагаются диффузными, и значения потоков не меняются по ответствующим поверхностям.
- поток от первого тела, достигший поверхности второго тела. Излучаемые потоки предполагаются диффузными, и значения потоков не меняются по ответствующим поверхностям.
Свойство взаимности угловых коэффициентов:
 , (10. 4)
, (10. 4)
|
|
|
где 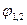 ,
,  - средние угловые коэффициенты излучения первого и второго тел;
- средние угловые коэффициенты излучения первого и второго тел; 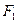 ,
, 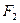 - площади поверхности первого и второго тел.
- площади поверхности первого и второго тел.
Угловые коэффициенты излучения определяются в зависимости от геометрических параметров и способа размещения двух тел в пространстве:
1) два параллельных диска с центрами на общей нормали и одинаковыми диаметрами d (рис. 10. 1):
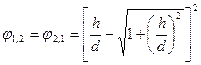 , (10. 5)
, (10. 5)
где h – расстояние между дисками;

Рис. 10. 1. Лучистый теплообмен между дисками
2) два параллельных диска с центрами на общей нормали, но разными диаметрами, 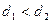 :
:
 ;
;
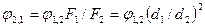 ; (10. 6)
; (10. 6)
3) две параллельные пластины одинаковой ширины а (рис. 10. 2):
 , (10. 7)
, (10. 7)
где h – расстояние между поверхностями пластин;

Рис. 10. 2. Лучистый теплообмен между параллельными пластинами
4) стенка с расположенным на ней рядом труб с наружным диаметром d и шагом s (рис. 10. 3):
 ; (10. 8)
; (10. 8)
 - условие взаимности угловых коэффициентов лучеиспускания за 1 м длины трубы.
- условие взаимности угловых коэффициентов лучеиспускания за 1 м длины трубы.
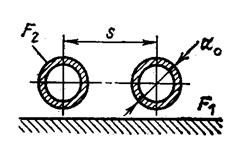
Рис. 10. 1. Лучистый теплообмен между трубами и стенкой
Приведенный коэффициент теплового излучения  системы двух тел определяется с помощью коэффициента теплового излучения
системы двух тел определяется с помощью коэффициента теплового излучения  первого и
первого и 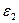 второго тел, расположенных следующими способами:
второго тел, расположенных следующими способами:
1) два тела, произвольно расположенных в пространстве (общий случай):
 ; (10. 9)
; (10. 9)
2) два тела с параллельными поверхностями больших размеров, угловые коэффициенты  , и формула (10. 9) принимает вид
, и формула (10. 9) принимает вид
 ; (10. 10)
; (10. 10)
3) тело с площадью поверхности 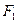 находится внутри другого тела с площадью поверхности
находится внутри другого тела с площадью поверхности 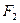 . Угловые коэффициенты
. Угловые коэффициенты  ,
, 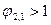 . С учетом (10. 4) формула (10. 9) принимает вид
. С учетом (10. 4) формула (10. 9) принимает вид
 . (10. 11)
. (10. 11)
При  имеем
имеем  , тогда
, тогда  ;
;
4) при наличии n плоских экранов, расположенных между двумя телами с параллельными поверхностями больших размеров,
 , (10. 12)
, (10. 12)
где 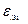 - коэффициент теплового излучения i-гo экрана;
- коэффициент теплового излучения i-гo экрана;
|
|
|
5) при наличии п цилиндрических экранов, расположенных между телом и внешней оболочкой,
 , (10. 13)
, (10. 13)
где  ,
,  ,
, 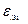 - коэффициенты теплового излучения соответственно тела, внешней оболочки и i-гo экрана;
- коэффициенты теплового излучения соответственно тела, внешней оболочки и i-гo экрана; 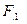 ,
,  ,
,  - площади поверхностей соответственно тела, внешней оболочки и i-гo экрана.
- площади поверхностей соответственно тела, внешней оболочки и i-гo экрана.
Закон Вина:
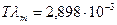 , (10. 14)
, (10. 14)
где Т - температура тела, К;  - длина волны, соответствующая максимуму спектральной интенсивности излучения, м.
- длина волны, соответствующая максимуму спектральной интенсивности излучения, м.
Закон Кирхгофа:
 (10. 15)
(10. 15)
где  ,
,  - плотности потоков собственного излучения реального абсолютно черного тела в условиях теплового равновесия; А - коэффициент поглощения реального тела.
- плотности потоков собственного излучения реального абсолютно черного тела в условиях теплового равновесия; А - коэффициент поглощения реального тела.
Для серого тела в условиях теплового равновесия интегральные характеристики 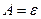 .
.
Эффективное  и результирующее
и результирующее  излучения тела определяются соотношениями
излучения тела определяются соотношениями
 (10. 16)
(10. 16)
 (10. 17)
(10. 17)
где Е - собственное излучение тела, К; А - коэффициенты отражения и поглощения тела;  плотность падающего извне теплового излучения на тело.
плотность падающего извне теплового излучения на тело.
Лучисто – конвективный теплообмен между двумя телами с температурами  и
и 
 :
:
1) тепловой поток  , Вт, и его плотность
, Вт, и его плотность  , Вт/м2,
, Вт/м2,
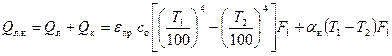 ; (10. 18)
; (10. 18)
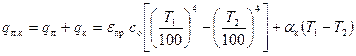 ; (10. 19)
; (10. 19)
или
 (10. 20)
(10. 20)
где 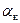 - коэффициент конвективной теплоотдачи, определенный без учета влияния лучистого теплообмена (рассчитывается по формулам для свободного или вынужденного движения среды);
- коэффициент конвективной теплоотдачи, определенный без учета влияния лучистого теплообмена (рассчитывается по формулам для свободного или вынужденного движения среды); 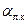 - коэффициент лучисто-конвективной теплоотдачи
- коэффициент лучисто-конвективной теплоотдачи  ;
;
2) условный коэффициент теплоотдачи излучением, Вт/ 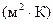 ,
,
 . (10. 21)
. (10. 21)
|
|
|


