 |
Изменение моментов инерции при повороте координатных осей
|
|
|
|
Пусть нам известны собственные моменты инерции 
, 
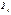и 
относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси 
и 
, повернутые относительно осей x и y на угол 
. Будем считать этот угол положительным при повороте осей координат против хода часовой стрелки.
Моменты инерции поперечного сечения при повороте осей координат определяются по формулам:
;
.
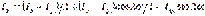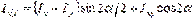Из формул моментов инерции при повороте осей координат видно, что сумма собственных осевых моментов инерции не изменяется при повороте координатных осей: 
Две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда из третьей формулы моментов инерции при повороте осей координат легко можно определить направление этих осей:
Нормальные и касательные напряжения при поперечном изгибе.
При поперечном изгибе в сечении балки помимо изгибающего момента (
) возникает поперечная сила (
). Поэтомув поперечном сечении при поперечном изгибе наряду с нормальными напряжениями (
) возникают и касательные напряжения (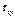
).
Касательные напряжения возникают и в продольных сечениях балки. Вследствие этого при поперечном изгибе отмечаются сдвиги продольных слоев балки относительно друг друга.
Исследования показали: если балка является достаточно длинной, влияние искривления поперечного сечения на значения нормальных напряжений невелико, поэтому влиянием сдвигов на закон распределения нормальных напряжений при изгибе пренебрегают, формула нормальных напряжений при поперечном изгибе: 
.
|
|
|
Проанализируем формулу Журавского: 
Поперечная сила (
) для конкретного сечения и момент инерции поперечного сечения относительно нейтральной оси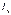 
являются постоянными величинами, поэтому касательные напряжения изменяются по высоте поперечного сечения по тому же закону, что и отношение статического момента отсеченной части поперечного сечения (
) к ширине поперечного сечения (
), в котором они вычисляются.
Во всех точках поперечного сечения, расположенных на расстоянии y от нейтральной линии (по всей ширине сечения 
), касательные напряжения при поперечном изгибе одинаковы.
В самых удаленных от нейтральной оси точках поперечного сечения касательные напряжения при поперечном изгибе равны 0, поскольку в этом случае 
.
Наибольшие касательные напряжения возникают в точках поперечного сечения, расположенных на нейтральной оси. Напомним, что в этих точках нормальные напряжения равны нулю
Билет 6.
Главные моменты Инерции
При повороте центральных осей и приближении их к главным центральным осям, больший из собственных осевых моментов инерции становится еще больше, стремясь к максимальному значению (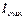
), а меньший – меньше, приближаясь к минимальному значению (
).
Главные центральные моменты инерции - моменты инерции фигуры относительно главных центральных осей 
и 
. Формулыглавных центральных моментов инерции, вытекающих из формул моментов инерции при повороте осей координат:
Если в частном случае 
, то осевые моменты инерции при повороте координатных осей вообще не изменяются, и тогда любые две взаимно перпендикулярные оси, проходящие через центр тяжести поперечного сечения, являются главными центральными осями.
|
|
|
