 |
Расчет балок на прочность при изгибе
|
|
|
|
Расчет балок на прочность обычно ведется по наибольшим нормальным напряжениям, возникающим в их поперечных сечениях. Условие прочности по нормальным напряжениям 
где 
– наибольшее по модулю напряжение в поперечном сечении; 
– изгибающий момент; 
– осевой момент сопротивления; 
– допускаемые нормальные напряжения.
При расчете на прочность элементов конструкций, работающих на изгиб, возможны три следующих вида задач:
а) проверка напряжений (проверочный расчет);
б) подбор сечения (проектный расчет);
в) определение допускаемой нагрузки (определение грузоподъемности).
Методика решения этих задач для балок из пластичных и хрупких материалов различна, так как балки из пластичных материалов одинаково работают на растяжение и сжатие, а из хрупких материалов лучше работают на сжатие, чем на растяжение. Это влияет на применяемые формы поперечных сечений балок и на способ определения опасного сечения.
Известные различия имеются также в расчетах балок постоянного по всей длине и переменного поперечного сечения.
Кроме того, следует иметь в виду, что в некоторых (сравнительно редких) случаях расчет на прочность только по наибольшим нормальным напряжениям, действующим в поперечном сечении балки, недостаточен, и приходится дополнительно производить проверку прочности также по главным напряжениям, возникающим в наклонных сечениях, и по максимальным касательным напряжениям.Условие прочности по касательным напряжениям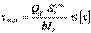 
где 
– наибольшее по модулю напряжение в поперечном сечении; 
– допускаемые касательные напряжения.
Если для материала балки заданы различные допускаемые нормальные напряжения при растяжении и сжатии, то условия прочности применяют отдельно к наиболее растянутым и к наиболее сжатым волокнам балки.
|
|
|
Билет 7
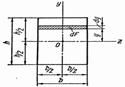
Прямоугольное сечение
Определим осевой момент инерции прямоугольника высотой h и шириной b относительно оси z 
проходящей через его основание (рис. 11.5, а). Выделим из прямоугольника линиями, параллельными оси z 
элементарную полоску высотой z 
и шириной b. 
Площадь этой полоски 
расстояние от полоски до оси z1 равно y1. Подставим эти величины в выражение момента инерции (8.5): 
Аналогичным путем для момента инерции относительно оси y1 можно получить выражение
Для определения центробежного момента инерции Iy1z1 выделим из прямоугольника линиями, параллельными осям z1 и y1 (рис.
11.5, б), элементарную площадку величиной 
. Определим сначала центробежный момент инерции не всего прямоугольника, а лишь вертикальной полоски высотой h и шириной dz1 расположенной на расстоянии z1 от оси y
Произведение z1dz1 вынесено за знак интеграла, так как для всех площадок, принадлежащих рассматриваемой
вертикальной полоске, оно постоянно.
Проинтегрируем затем выражение dIy1z1 в пределах от z1=0 до z1=b
Определим теперь осевые моменты инерции прямоугольника относительно осей у и z, проходящих через центр тяжести параллельно сторонам прямоугольника (рис. 12.5). Для этого случая пределы интегрирования будут от y = - h/2 до y = h/2
Следовательно, 
Аналогично 
Центробежный момент инерции прямоугольника относительно осей y и z (рис. 12.5) равен нулю, так как эти оси совпадают с его осями симметрии.
2) Дифференциальное уравнение изогнутой оси балки и его интегрирование.
При изгибе ось балки искривляется, а поперечные сечения перемещаются поступательно и поворачиваются вокруг нейтральных осей, оставаясь при этом нормальными к изогнутой продольной оси (рис. 8.22). Деформированная (изогнутая) продольная ось балки называется упругой линией, а поступательные перемещения сечений, равные перемещениям y=y(x) их центров тяжести сечений – прогибами балки.
|
|
|
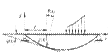Между прогибами y(x) и углами поворота сечений θ(x) существует определенная зависимость. Из рис. 8.22 видно, что угол поворота сечения θ равен углу φ наклона касательной к упругой линии (θ и φ - углы с взаимноперпендикулярными сторонами). Но согласно геометрическому смыслу первой производной y/=tgθ. Следовательно, tgθ = tgφ = y/.
В пределах упругих деформаций прогибы балок обычно значительно меньше высоты сечения h, а углы поворота θ не превышают 0.1 – 0.15 рад. В этом случае связь между прогибами и углами поворота упрощается и принимает вид θ = y/.
Определим теперь форму упругой линии. Влияние перерезывающих сил Q на прогибы балок, как правило, незначительно. Поэтому с достаточной точностью можно принять, что при поперечном изгибе кривизна упругой линии зависит только от величины изгибающего момента Mz и жесткости EIz (см. уравнение (8.8)):
 .
| (8.26) |
В то же время в неподвижной системе координат кривизна упругой линии, как и всякой плоской кривой,
 .
| (8.27) |
Приравнивая правые части (8.26) и (8.27) и учитывая, что правила знаков для Mz и y // были приняты независимо друг от друга, получаем
 .
| (8.28) |
Это равенство называется дифференциальным уравнением упругой линии. При малых деформациях второе слагаемое в знаменателе мало по сравнению с единицей (при θ = 0.1 рад (y / )2=0.01) и им можно пренебречь. В результате получим приближенное дифференциальное уравнение упругой линии балки
 .
| (8.29) |
Выбор знака в правой части (8.29) определяется направлением координатной оси y, так как от этого направления зависит знак второй производной y //. Если ось направлена вверх, то, как видно из рис. 8.23, знаки y // и Mz совпадают, и в правой части надо оставить знак плюс. Если же ось направлена вниз, то знаки y // и Mz противоположны, и это заставляет выбрать в правой части знак минус.
Заметим, что уравнение (8.29) справедливо только в пределах применимости закона Гука и лишь в тех случаях, когда плоскость действия изгибающего момента Mz содержит одну из главных осей инерции сечения.
Интегрируя (8.29), находим сначала углы поворота сечений 
а после второго интегрирования – прогибы балки 
|
|
|
Постоянные интегрирования определяются из граничных условий. На участках с различными аналитическими выражениями для изгибающих моментов дифференциальные уравнения упругой линии также различны. Интегрирование этих уравнений при n участках дает 2n произвольных постоянных. Для их определения к граничным условиям на опорах добавляются условия равенства прогибов и углов поворота на стыке двух смежных участков балки.
Билет 8
1) Треугольное сечение
Определим осевые моменты инерции треугольника относительно трех параллельных осей z1, z0, z 2, проходящих через его основание (рис. 13.5, а), центр тяжести (рис. 13.5,б) и вершину (рис. 13.5, е).
Для случая, когда ось проходит через основание треугольника (рис. 13.5, а),
Для случая, когда ось проходит через центр тяжести треугольника параллельно его основанию (рис. 13.5, б),
В случае, когда ось проходит через вершину треугольника параллельно его основанию (рис. 13.5, в),
2) Метод непосредственного интегрирования
Метод интегрирования, при котором данный интеграл путем тождественных пpeобpaзoвaний подынтегральной фyнкции (или выражения) и применения свойств нeoпpеделeннoгo интеграла приводится к oдиoмy или нескольким табличным интегралам, называется нeпоcpeдcтвeнным uнmeгpирoванием.
При сведении даннoгo интеграла к табличному часто используются следующие пpeoбpазoвания диффeренциaлa (операция «подвeдeния под знак дuффepeнциала»):
Boобщe, ƒ'(u)du=d(ƒ(u)), эта формула очень частo используется при вычислении интегралов.
Билет 9.
|
|
|
