 |
Осевой момент инерции круга.
|
|
|
|
Осевой момент инерции фигуры - этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси.
Подсчитываем сначала полярный момент инерции круга. Для этого выделим в сечении окружностями радиусами 
ЭЛЕМНЕТАРНОЕ КОЛЬЦО ПЛОЩАДЬЮ 
и вычислим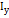 
по формуле:
Обычно размеры круглого сечения выражают через диаметр d и подсчитывают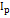 
по формуле
осевые моменты инерции круга найдем с помощью отношения 
. Замечая, что в силу симметрии круга 
, получаем для осевы моментов инерции круга выражение:
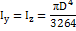
Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
Метод начальных параметров.
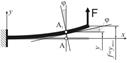
Прогиб (y) - смещение центра тяжести балок по направлению, перпендикулярному к её оси;
Угол поворота сечения (φ) - угол, на который сечение поворачивается относительно своего первоначального положения (или угол между касательной к упругой линии и первоначальной осью балки)
Суть метода начальных параметров применительно к расчету собственных колебаний стержневой системы заключается в том, что по известным значениям перемещений (прогиб, угол поворота) и внутренних сил (поперечная сила, изгибающий момент) в начале участка в соответствии с определенным алгоритмом находят значения этих переменных в конце участка.
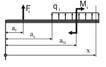
Позволяет при любом числе участков балки свести решение к отысканию всего двух констант - прогиба и угла по ворота в начале координат. Для реализации метода начальных параметров необходимо при составлении уравнении моментов по участкам и интегрировании этого уравнения придерживаться следующих правил:
|
|
|
1. Начало координат необходимо выбирать общим для всех участков в крайней левой точке балки;
2. Все составляющие уравнения моментов на предыдущем участке должны сохраняться неизменными в уравнении моментов последующих участков;
3. В случае обрыва распределенной нагрузки её продлевают до конца балки, а для восстановления действительных условий нагружения вводят "компенсирующую" нагрузку обратного направления;
4. Интегрировать уравнения на всех участках следует, не раскрывая скобок.
Окончательные универсальные уравнения метода начальных параметров:
;
;
;
;
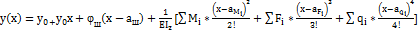Величина 
- угол поворота в промежуточном (подвесном) шарнире, при этом 
- координата шарнира.
- угол поворота и прогиб балки в начале координат;
- координаты точек приложения внешнего момента, силы или начало распределенной нагрузки.
При решении задач удобно записать универсальные уравнения для сначала для наиболее удаленного от начала координат участка, тогда уравнение для предыдущих участков легко получить, вычеркивая из полученного уравнения члены, учитывающие нагрузку на последующий участок.
Билет 10.
Осевой момент инерции кольца.
Осевой момент инерции фигуры - этоинтеграл произведений элементарных площадей на квадраты их расстояний до рассматриваемой оси.
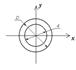
Осевой момент инерции кольца с внешним диаметром D и внутренним d относительно любой центральной оси может быть найден как разность моментов инерции большого и малого кругов:
≈ 0,05 
где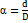 
- коэффициент полости.
Осевой момент инерции тела является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
|
|
|
