Напряжения в наклонных сечениях при растяжении и сжатии.

При растяжении бруса наклонные сечения, как и поперечные, остаются плоскими и параллельными. Следовательно, внутренние силы распределены по наклонным сечениям равномерно.

При растяжении:

При сжатии: .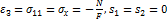

Напряжения в наклонных площадках наблюдаются, если мысленно «разрезать» стержень, растягиваемый силами P, наклонной плоскостью под углом к поперечному сечению (рис. 2.2, а), проходящей через точку K, и отбросить правую часть.

Внешняя нормаль к наклонномусечению будет составлять с осью угол . Действие отброшенной правой части стержня на левую часть заменим внутренними усилиями (рис. 2.2, б). Чтобы левая часть стержня находилась в равновесии, в каждой точке наклонного сечения стержня должно возникнуть продольное противодействующее усилие. Равнодействующая внутренних усилий N равна внешней силе P.

Допустим, внутренние усилия равномерно распределены по площади наклонного сечения . Тогда полное напряжение наклонного сечения в каждой точке будет равно:

где – нормальное напряжение, возникающее в точках (в том числе и в точке К), но в поперечном сечении стержня (рис. 2.1, в).

Разложим полное напряжение в наклонном сечении (p), возникающее в некоторой точке К, на две составляющие – нормальное () и касательное () напряжения (рис. 2.2, г). Они будут равны:

; .

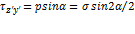Проследим, как будет меняться каждое из этих напряжений с изменением угла наклона сечения, проходящего через точку К, от нуля до 90̊.

При увеличении угла нормальное напряжение в точке К будет постепенно уменьшаться от своего максимального значения (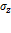) до нуля. Касательное напряжение при этом будет сначала возрастать от нулевого до максимального значения () при , а затем убывать и при угле снова станет равным нулю.

Следовательно, наибольшее нормальное напряжение действительно возникает в точках поперечного сечения стержня. В продольном сечении оно равно нулю. Следовательно, продольные волокна не давят друг на друга.

Наибольшие касательные напряжения возникают в наклонных сечениях, расположенных под углом 45̊ к оси стержня. В поперечном и продольном сечениях они равны нулю.

 

Теорема Максвелла.

Рассмотрим два состояния системы. В первом состоянии к систе­ме приложена сила P₁=1, а во втором — сила P₂=1 (рис. 5.12).

Обозначим перемещения, вызванные единичными силами или моментами (т. е. силами Р=1 или моментами М=1), знаком δ в отличие от перемещений, вызванных силами и моментами, не рав­ными единице, обозначаемых знаком ∆. В соответствии с этим пере­мещение рассматриваемой системы по направлению единичной силы. P₂ в первом состоянии (т. е. вызванное силой P₁=1) обозначим δ₂₁. а перемещение по направлению единичной силы P₁ во втором состоянии обозначим δ₁₂ (рис. 5.12).

На основании теоремы о взаимности работ для рассматриваемых двух состояний

но так как

То или в общем случае действия любых единичных сил (5.21)

Полученное равенство носит название теоремы о взаимности перемещений (теоремы, или принципа, Максвелла): для двух единичных состояний упругой системы перемещение по направлению первой единичной силы, вызванное второй единичной силой, равно перемещению по направлению второй силы, вызванному первой силой. Для иллюстрации теоремы Максвелла в качестве примера рас смотрим два состояния балки, изображенной на рис. 5.13.

В первом состоянии на балку действует сила Р=1, а во втором — момент Угол поворота ϑ_a, вызванный силой Р=1, на основании формулы (5.21) должен быть численно равен прогибу y_l вызванному моментом M=1, т. е. ϑ_a=y_l

Определим значения ϑ_a и y_l методом начальных параметров. В первом состоянии (рис. 5.13, а)

во втором состоянии (рис. 5.13,б)

При M=P=1

Т.е

Единичные перемещения (например, перемещения, вызванные отвлеченной единичной силой Р=1 или отвлеченным единичным моментом М=1) имеют размерности, отличные от обычных размер­ностей перемещений. Размерность единичного перемещения представ­ляет собой размерность отношения перемещения (не единичного) к вызвавшей его нагрузке. Так, например, в рассмотренном при­мере единичный угол поворота ϑa, вызванный силой P=1, выражен в 1/кН, единичный прогиб yl, вызванный моментом M=1, выражен в м/кН*м, или 1/кН, т. е. в тех же функциях, что и угол ϑa.

Билет №14.

⇐ Предыдущая12345678Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: